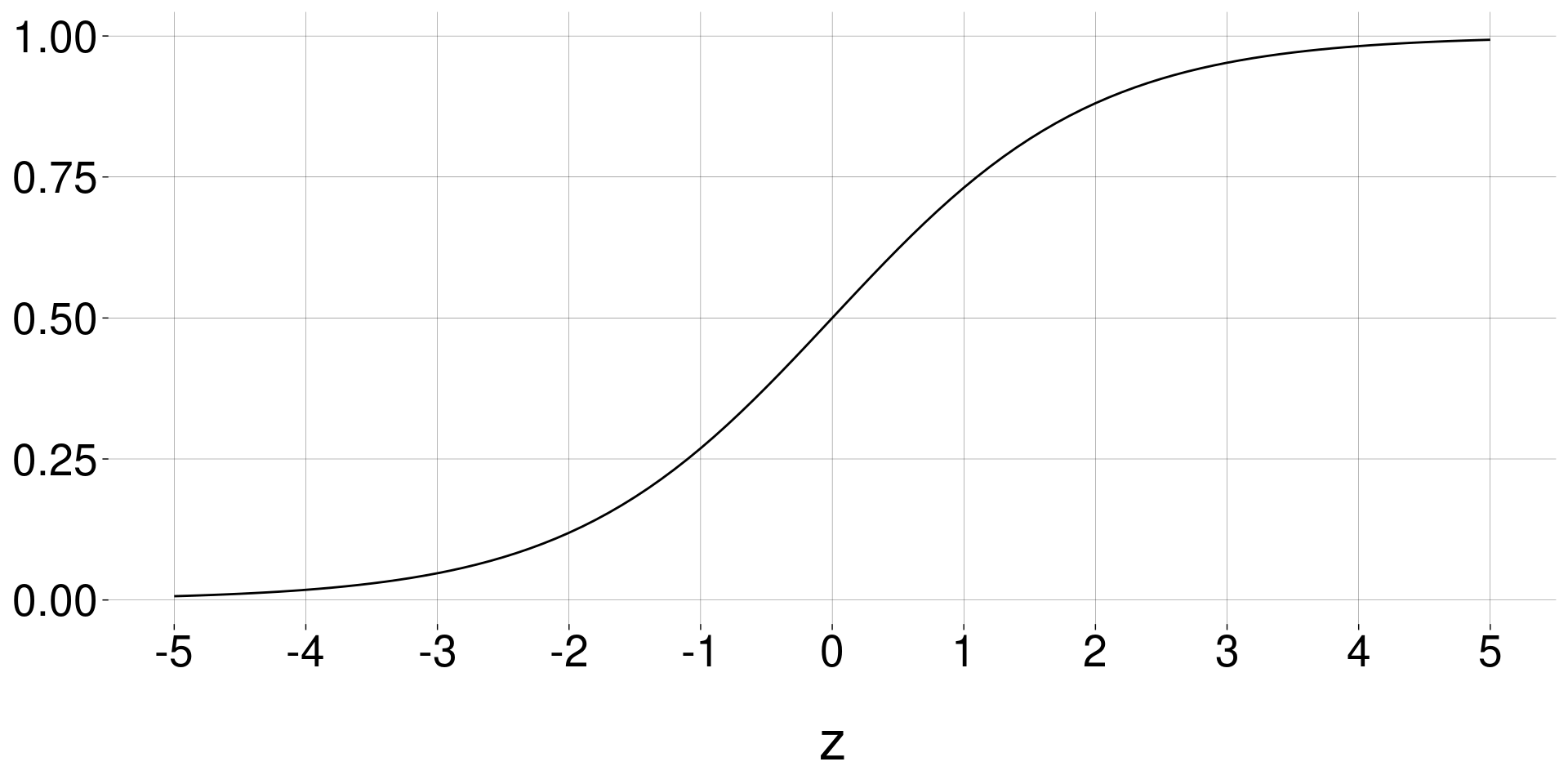
Redes Neurais: Primeiras Noções
(clique aqui para a transcrição)
13/12/2023
Rede neural com uma camada oculta
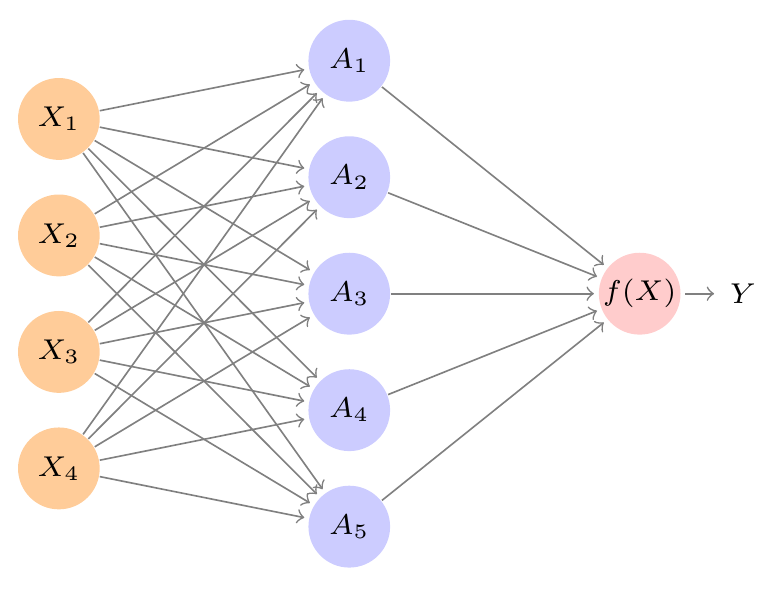
Imagem: James et al. (2021)
Rede neural com uma camada oculta
\(A_1 = h_1(\overrightarrow{X})\)
\(\phantom{A_1} = h_1(X_1, X_2, X_3, X_4)\)
\(\phantom{A_1} = g\;(w_{10} + w_{11} X_1 + w_{12} X_2 + w_{13} X_3 + w_{14} X_4)\)
\(\phantom{A_1} = g\left( w_{10} + \sum_{j=1}^4 w_{1j} X_j\right)\)
\(\mbox{}\)
O argumento de \(g\) é uma função linear de \(X_1, \ldots, X_4\),
mas a função \(g\) é não-linear.
Por exemplo, \(\quad \displaystyle g(z) = \frac{e^z}{1 + e^z}\;,\quad\) chamada função sigmóide.
(Se \(g\) também fosse linear, estaríamos fazendo regressão linear!)
Rede neural com uma camada oculta
\(A_i = h_i(\overrightarrow{X})\)
\(\phantom{A_i} = h_i(X_1, X_2, X_3, X_4)\)
\(\phantom{A_i} = g\;(w_{i0} + w_{i1} X_1 + w_{i2} X_2 + w_{i3} X_3 + w_{i4} X_4)\)
\(\phantom{A_i} = g\left( w_{i0} + \sum_{j=1}^4 w_{ij} X_j\right)\)
\(\mbox{}\)
\(Y = f(\overrightarrow{X})\)
\(\phantom{Y} = f(A_1, A_2, A_3, A_4, A_5)\)
\(\phantom{Y} = \beta_0 + \beta_1 A_1 + \beta_2 A_2 + \beta_3 A_3 + \beta_4 A_4 + \beta_5 A_5\)
\(\phantom{Y} = \beta_0 + \sum_{k=1}^5 \beta_k A_k\)
\(\phantom{Y ={}}\) (mas \(f\) também pode ser uma função não-linear.)
Rede neural com uma camada oculta
\(A_i = g\left(w_{i0} + \sum_{j=1}^4 w_{ij} X_j\right)\)
\(Y = \beta_0 + \sum_{k=1}^5 \beta_k A_k\)
-
Terminologia:
- Camada de entrada: \(\, X_j,\, 1 \leq j \leq 4\)
- Camada oculta: \(\, A_i,\, 1 \leq i \leq 5\)
- Função de ativação: \(\, g(\,)\)
- Camada de saída
-
Pesos (ou parâmetros):
- \(w_{ij},\, 1 \leq i \leq 5,\, 0 \leq j \leq 4\,\,\) (\(25\) parâmetros)
- \(\beta_k,\, 0 \leq k \leq 5\,\,\) (\(6\) parâmetros)
Exemplos de funções de ativação
ReLU (Rectified Linear Unit):
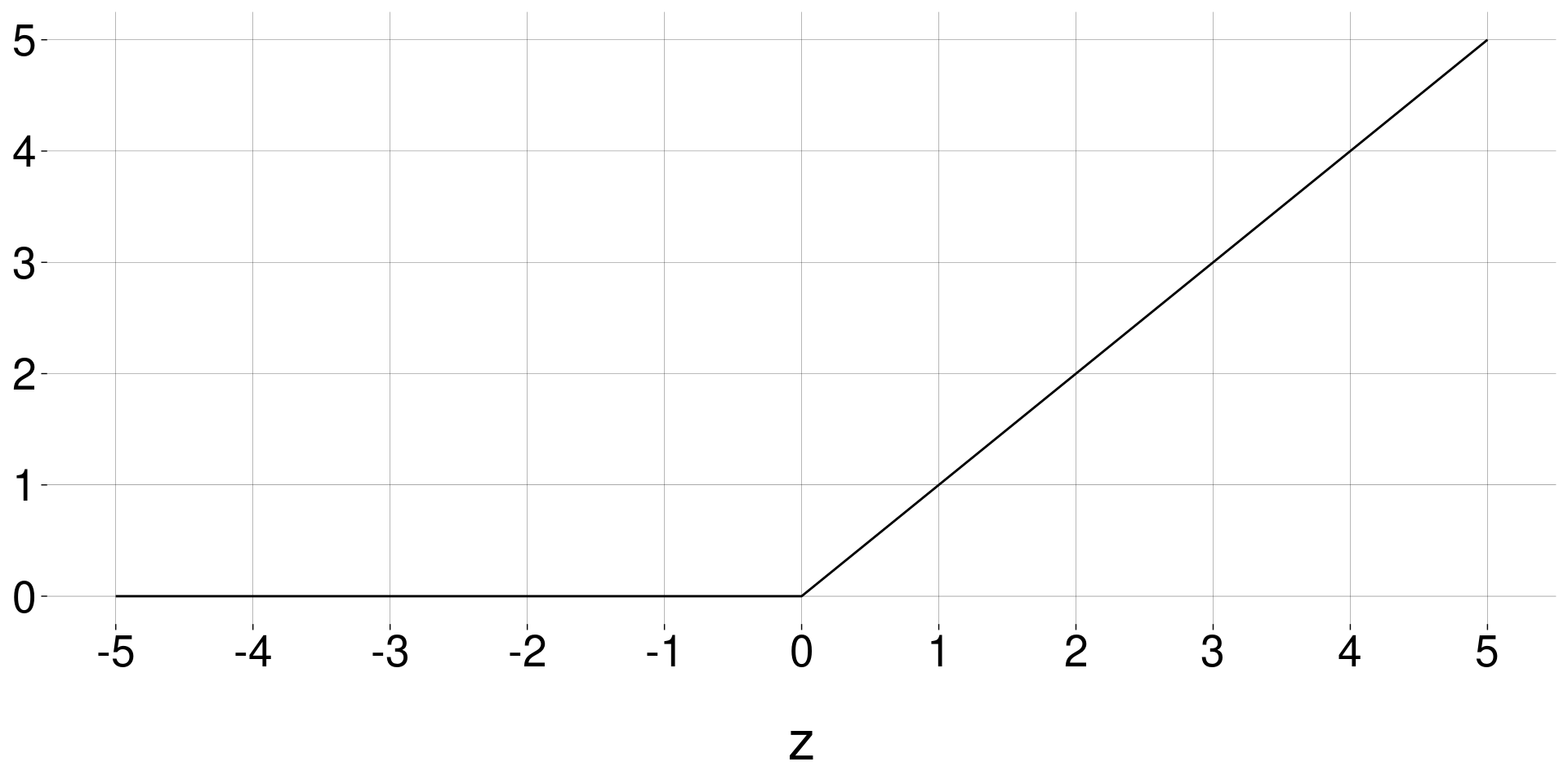
\[ \quad g(z) \quad=\quad \begin{cases} 0 &\text{ se } z < 0 \\ z &\text{ se } z \geq 0 \\ \end{cases} \quad=\quad \max(0, z) \]
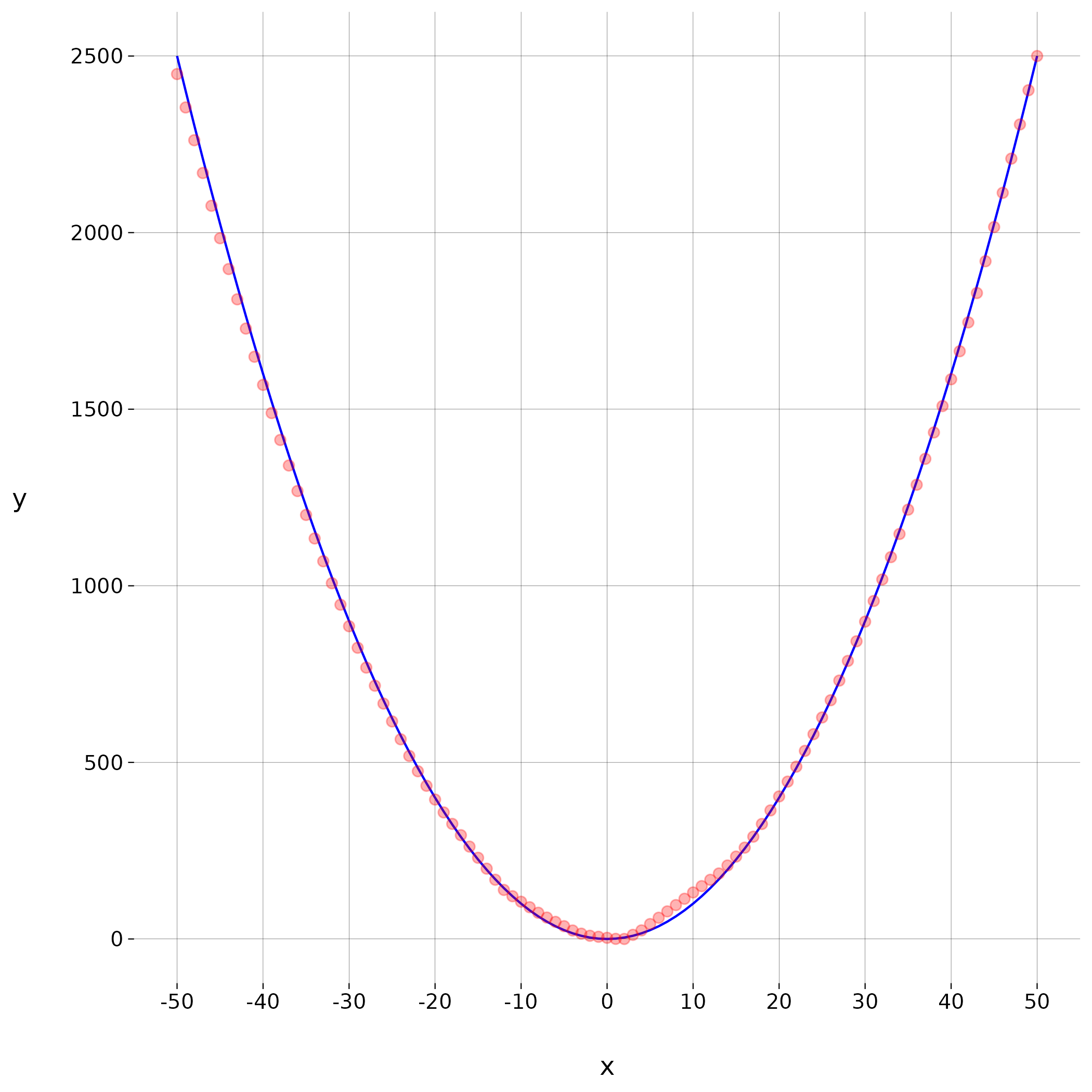
ReLUs aproximando uma função não-linear
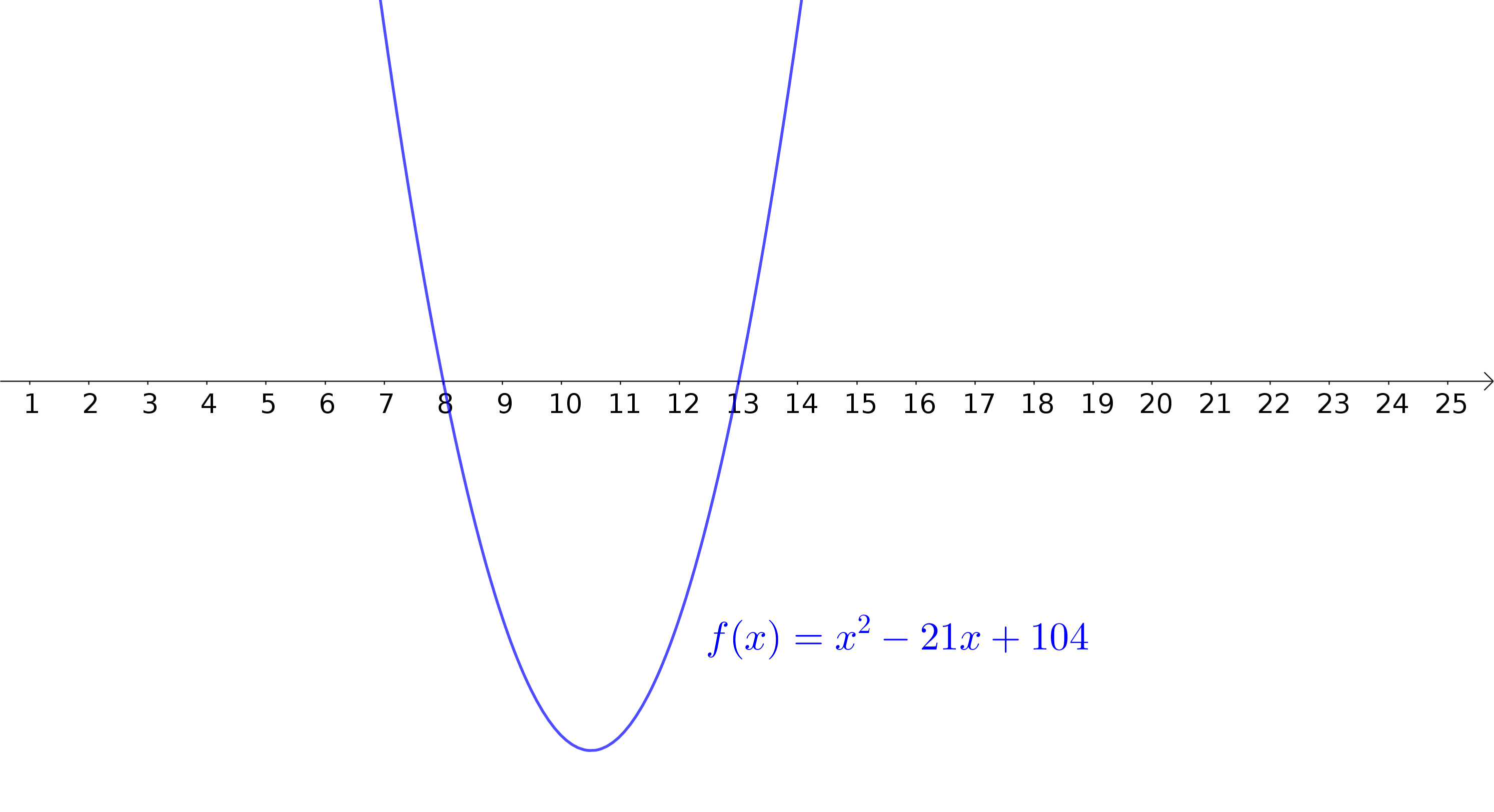
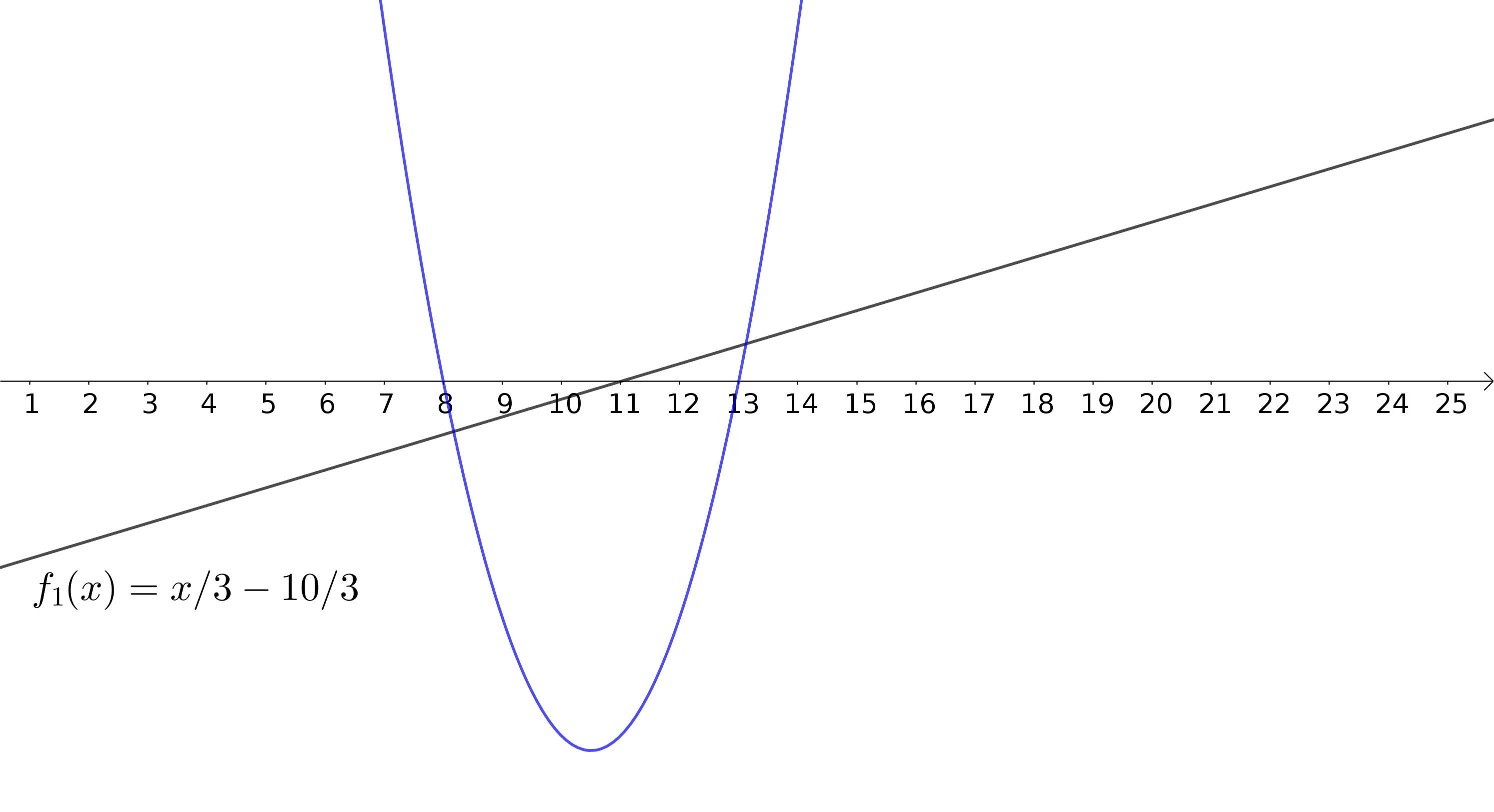
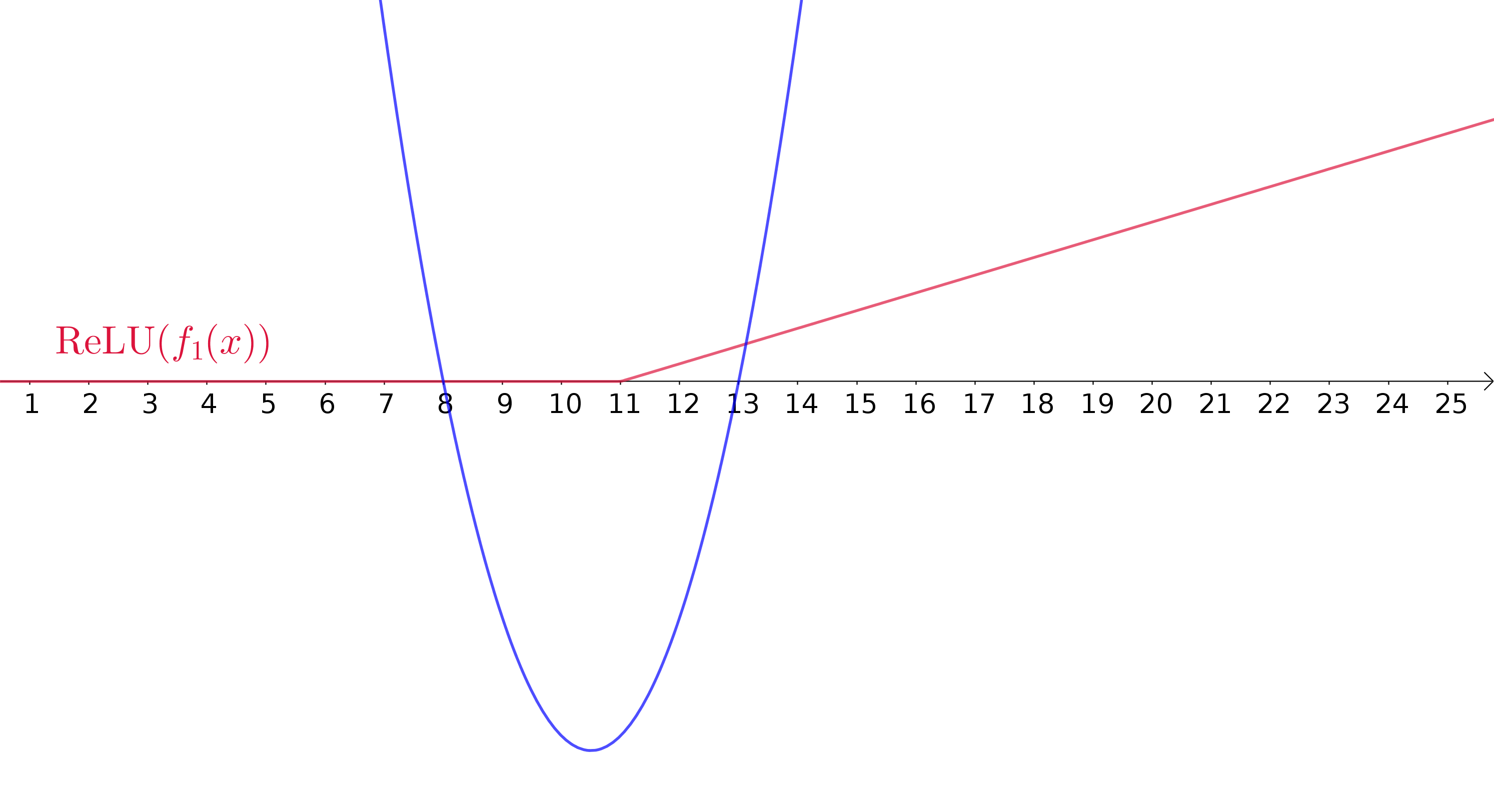
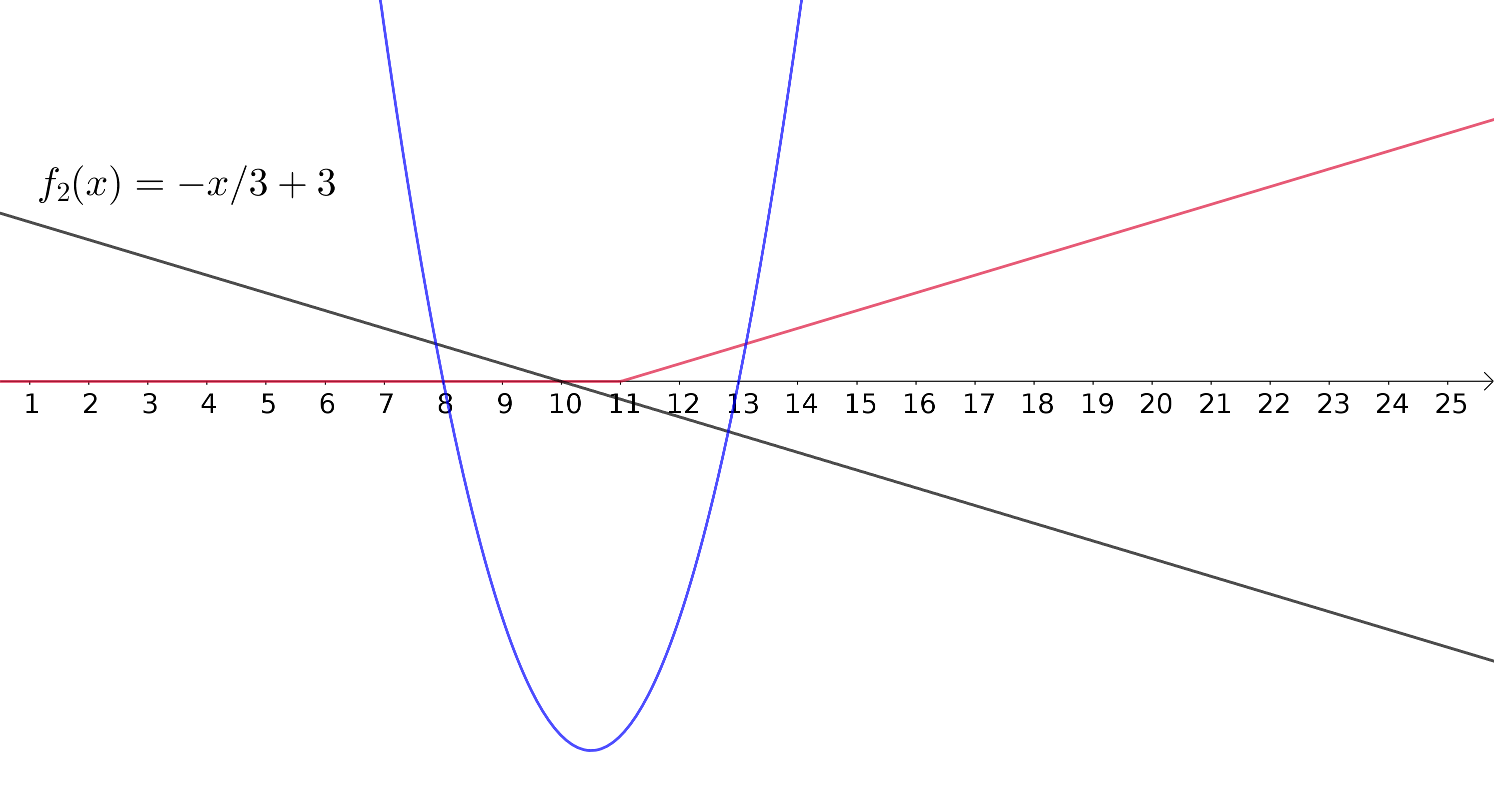
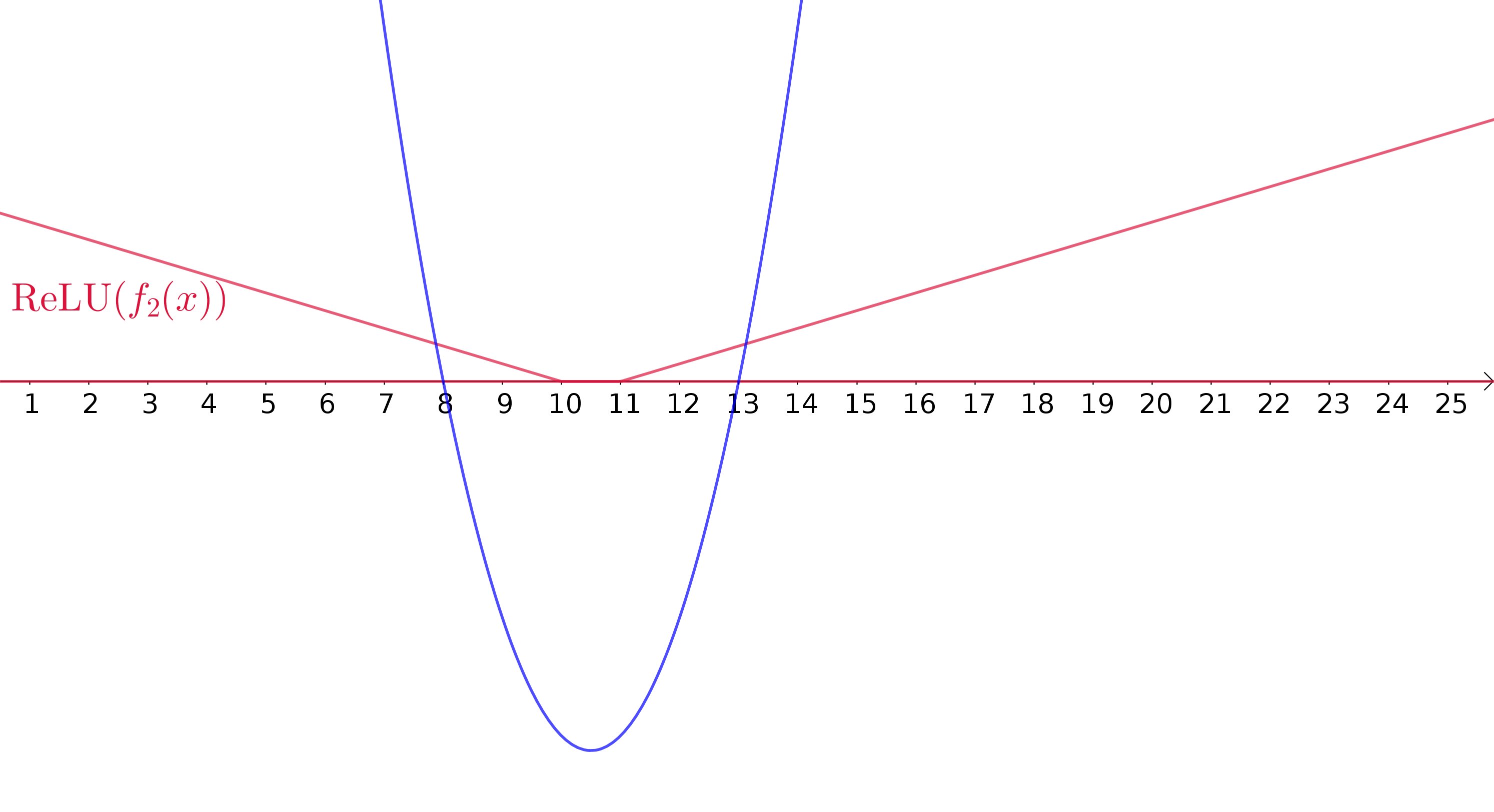
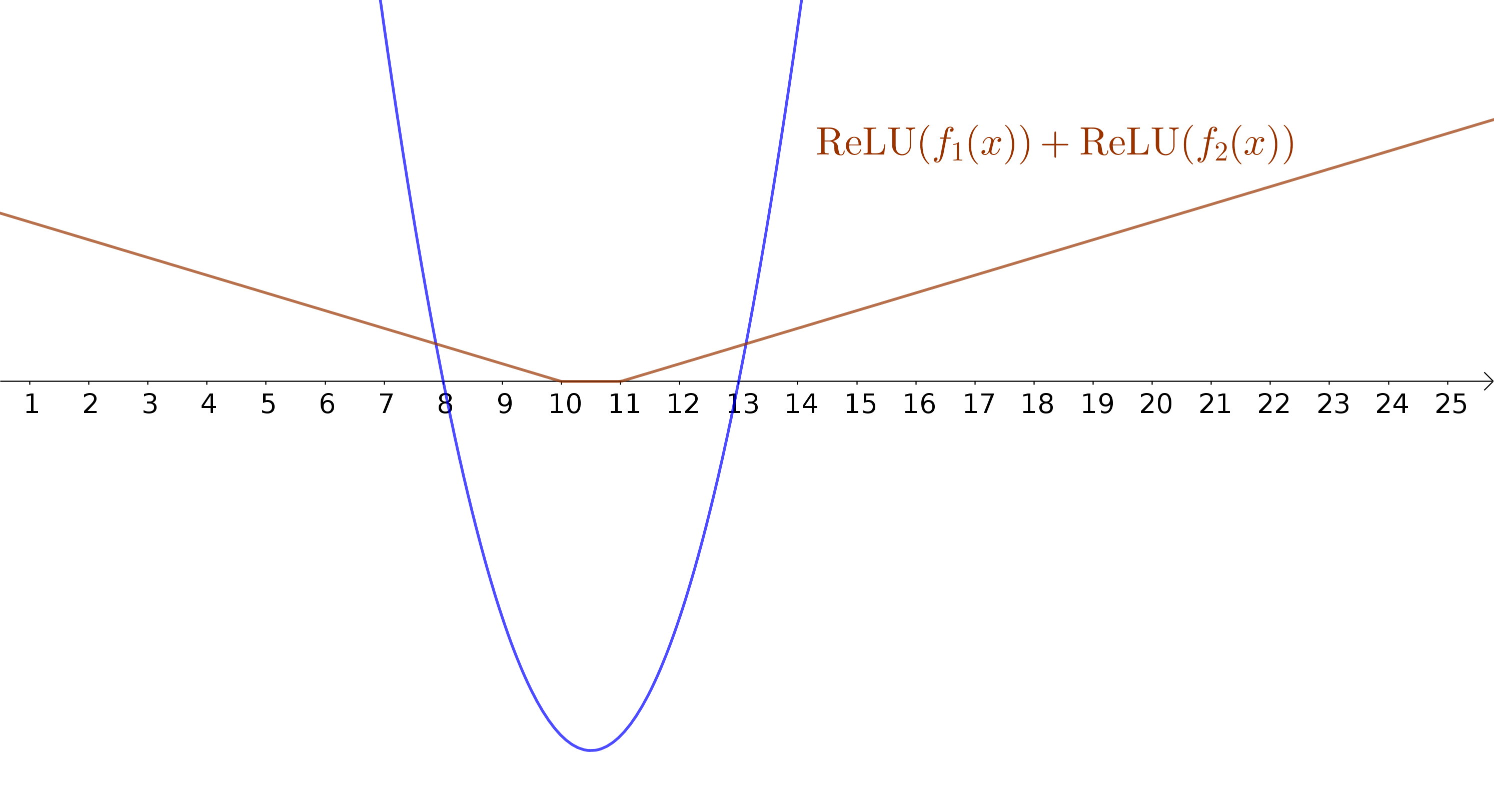
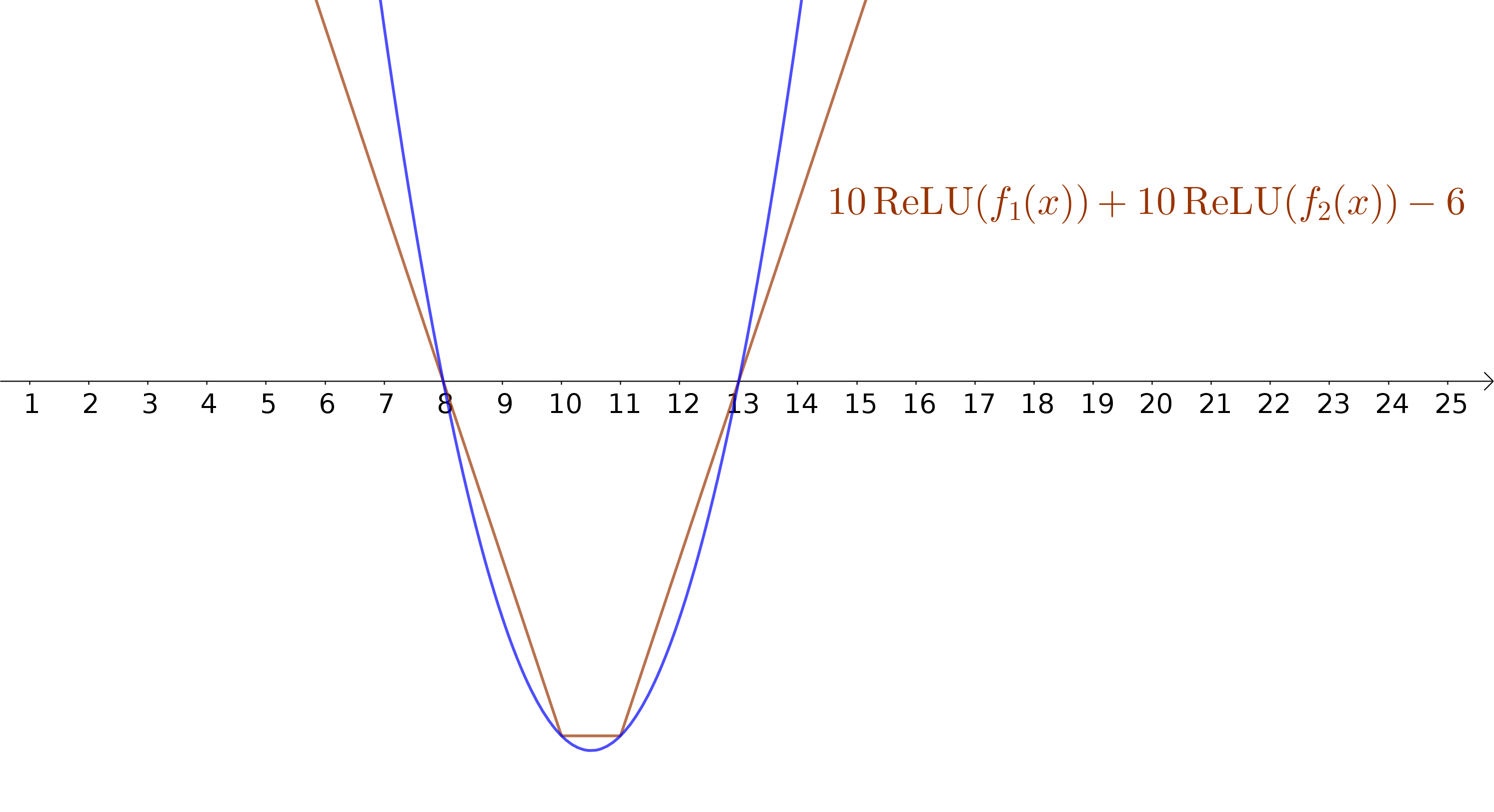
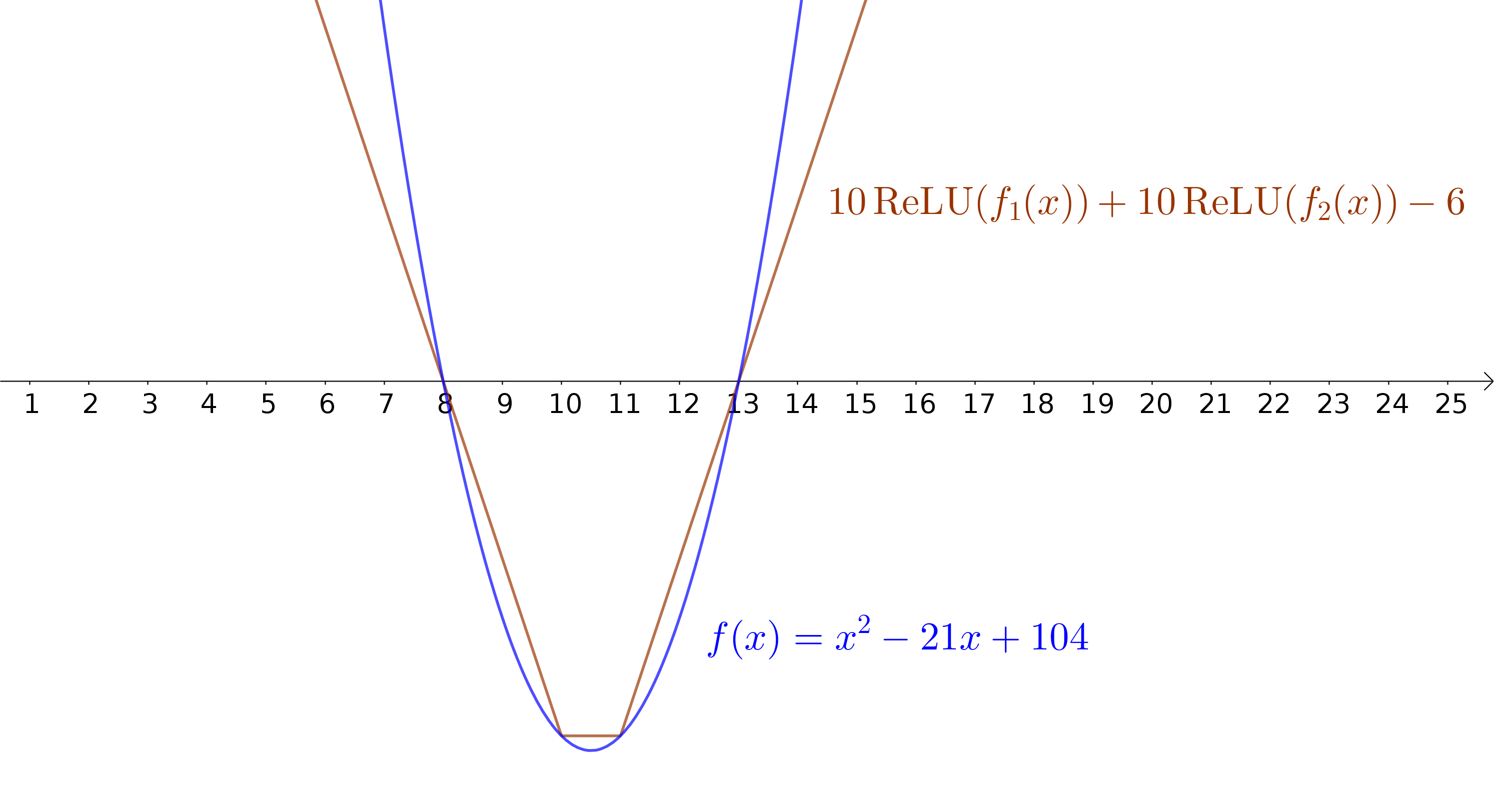
Aproximando uma função quadrática
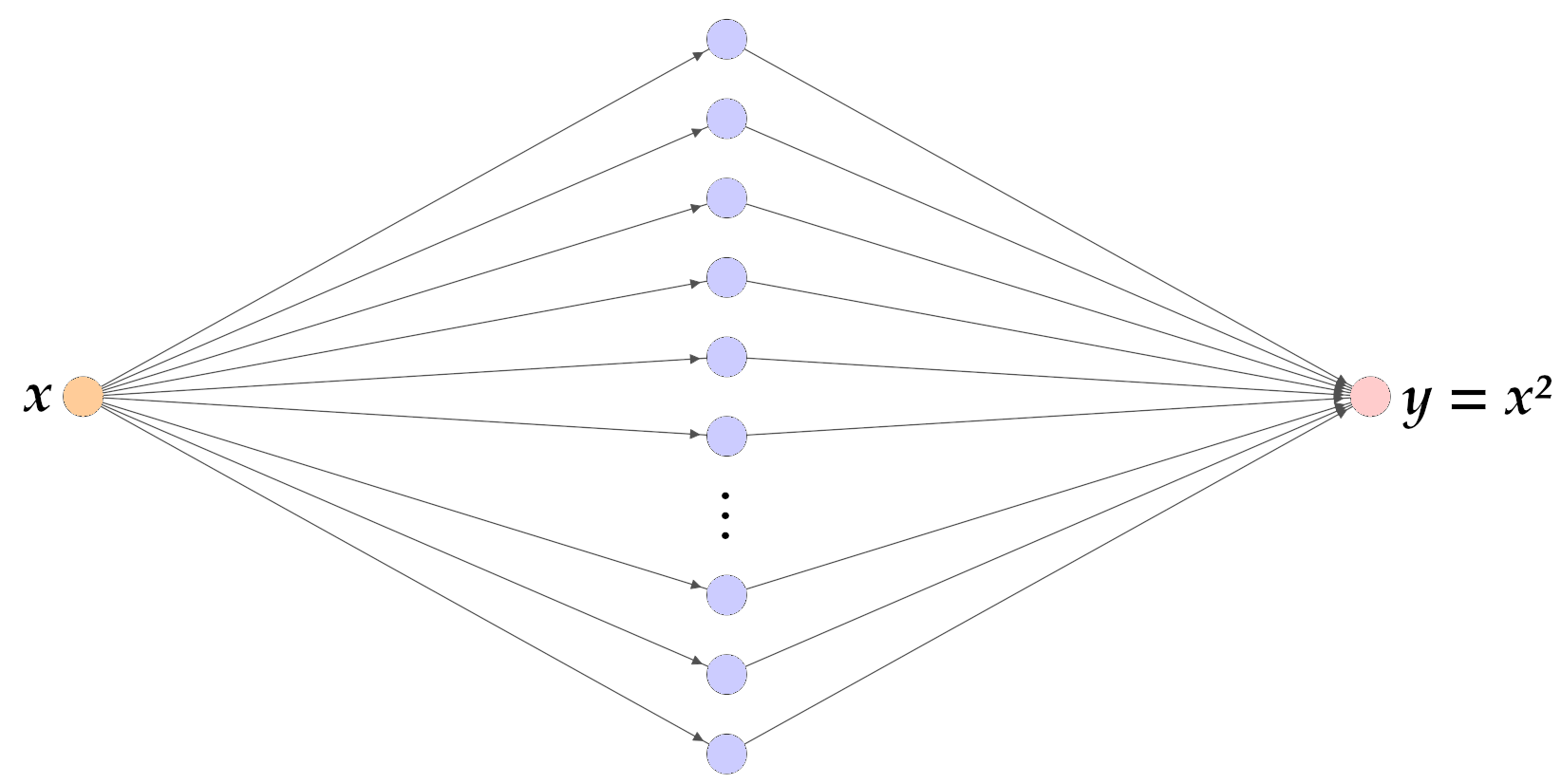
Uma camada oculta
\(200\) neurônios
ReLU como função de ativação
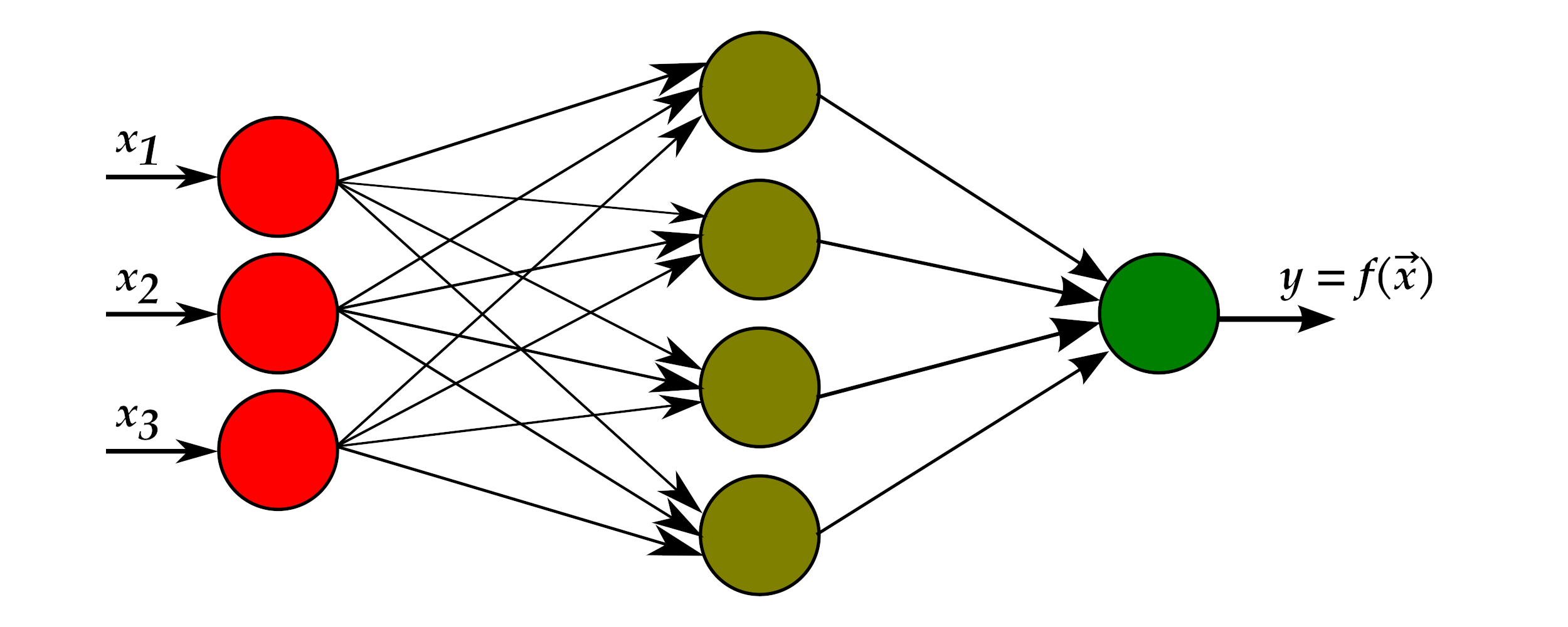
Regressão versus classificação
Regressão:
Classificação:
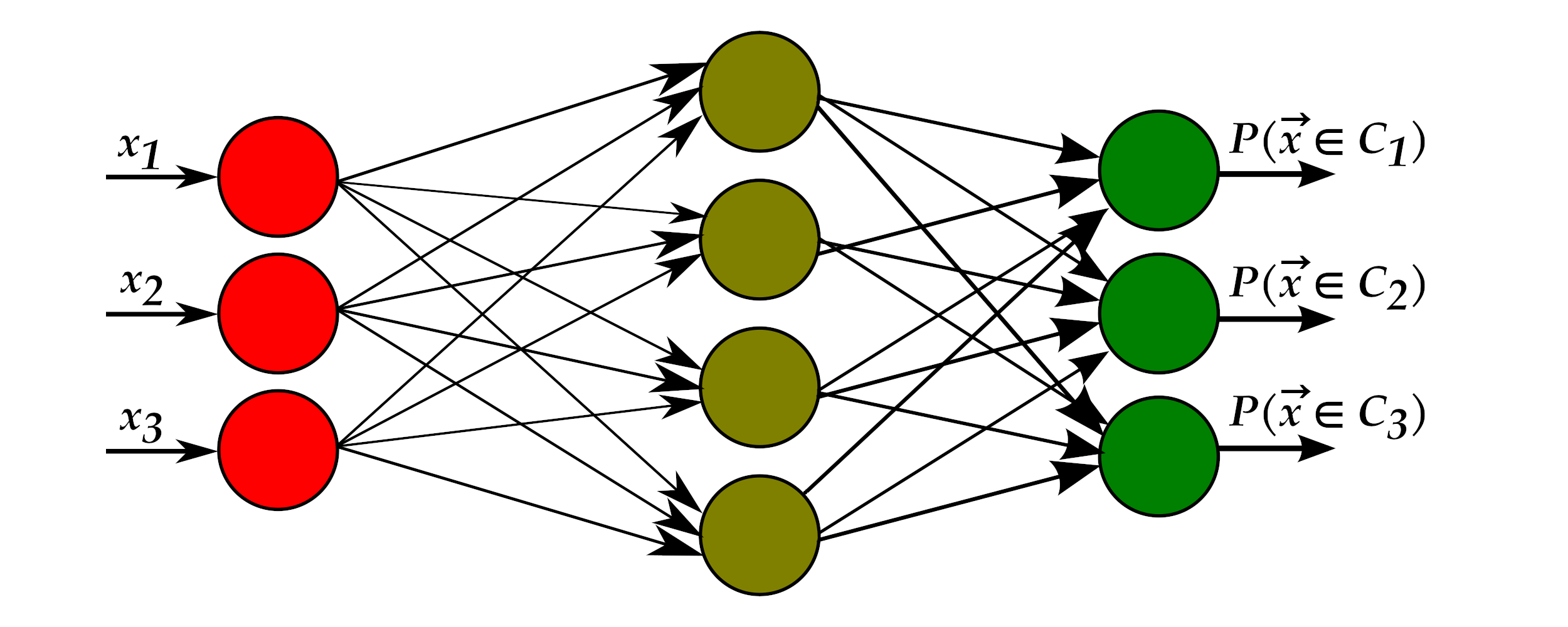
Imagem: https://commons.wikimedia.org/wiki/File:MultiLayerPerceptron.svg (CC BY SA)
O que falta ver?
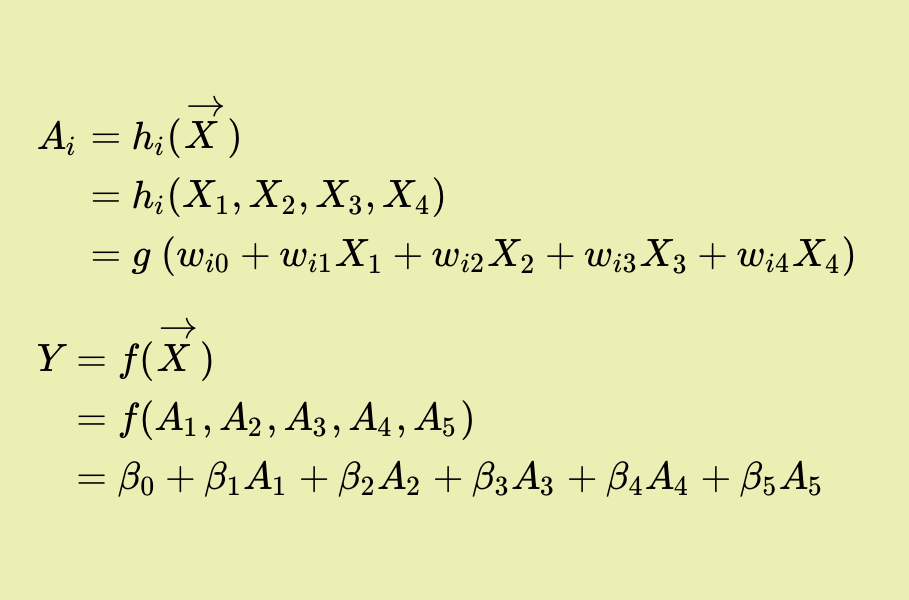
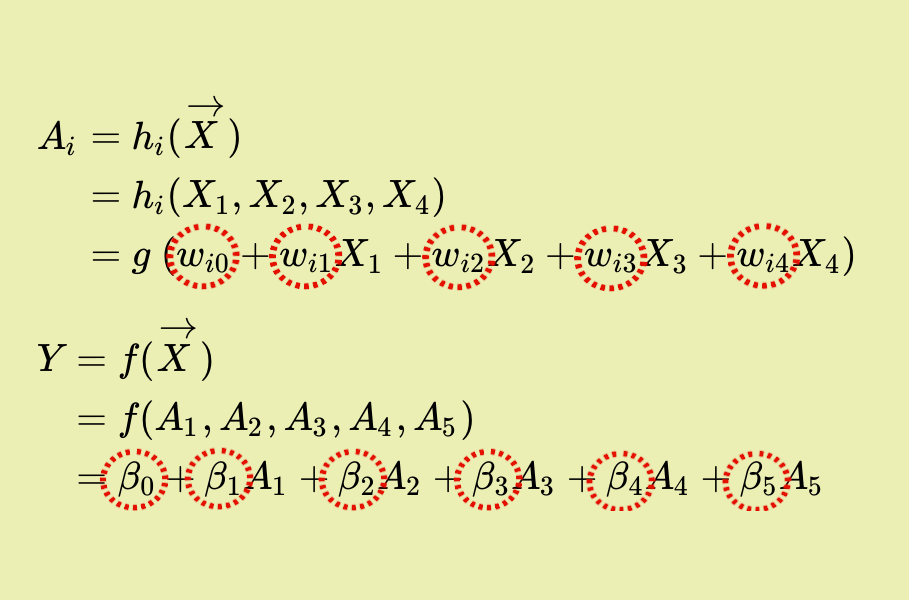
De onde vêm os valores destes pesos?