1 Primeiras noções sobre redes neurais
% vetor
1.1 Fonte
Este capítulo transcreve uma apresentação de slides que fiz sobre este assunto.
Boa parte do material apresentado aqui vem do capítulo 10 do livro James et al. (2021), que também está disponível online.
Você também pode assistir a uma playlist com mais de 100 vídeos, sobre os assuntos do livro James et al. (2021), apresentados pelos próprios autores.
1.2 Sumário

1.3 O que é uma rede neural
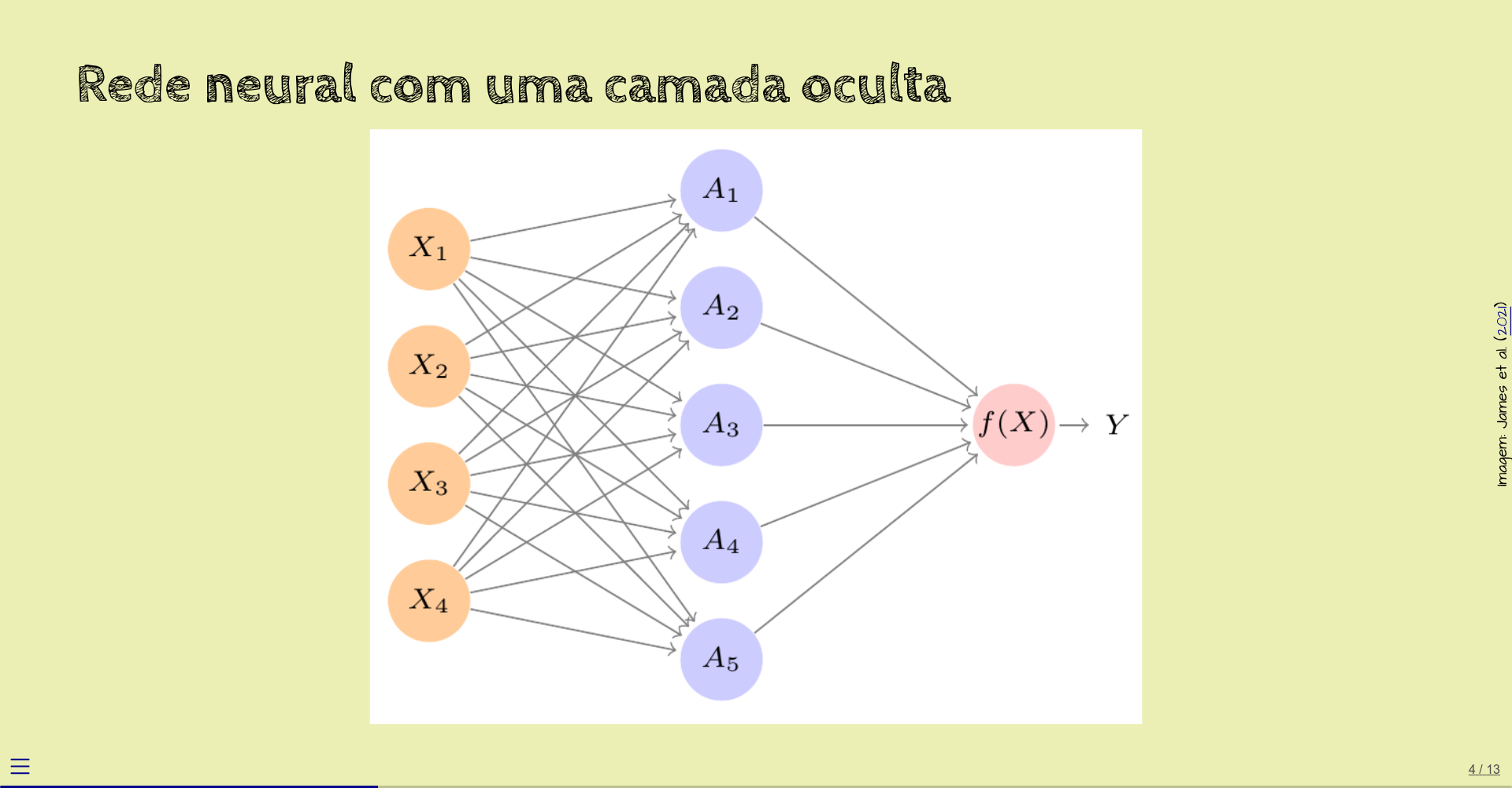
Neste diagrama, vemos um exemplo de rede neural com uma camada oculta.
Outros exemplos podem ter quantidades diferentes de camadas e de nós por camada.
Neste exemplo, os quatro nós à esquerda (\(X_1\) a \(X_4\)) representam simplesmente os valores dos dados de entrada da rede. Apesar de não acontecer nenhuma computação nestes nós, alguns livros consideram que estes nós formam a camada de entrada.
Os cinco nós azuis na coluna do meio (\(A_1\) a \(A_5\)) formam a camada onde a maior parte da computação acontece. É a camada oculta.
O nó cor-de-rosa à direita produz o valor de saída da rede. É a camada de saída. Nem sempre a camada de saída vai consistir de apenas um nó.
Estes nós também são chamados de neurônios, ou simplesmente unidades.
Cada nó produz um valor. As setas indicam como os valores dos nós são usados nas computações.
Por exemplo, o nó \(A_1\) calcula uma função dos quatro valores de entrada. Vamos chamar esta função de \(h_1\):
\[ A_1 = h_1(\overrightarrow{X}) = h_1(X_1, X_2, X_3, X_4) \]
(\(\overrightarrow{X}\) significa um vetor de valores, aqui com \(4\) elementos.)
A função \(h_1\) começa calculando a seguinte combinação linear dos elementos do vetor:
\[ w_{10} + w_{11} X_1 + w_{12} X_2 + w_{13} X_3 + w_{14} X_4 \]
Os coeficientes \(w_{ij}\) são chamados de pesos, ou parâmetros.
Você pode imaginar que, no diagrama, cada seta corresponde a um peso:
- \(w_{11}\) corresponde à seta de \(X_1\) para \(A_1\),
- \(w_{12}\) corresponde à seta de \(X_2\) para \(A_1\),
- \(w_{13}\) corresponde à seta de \(X_3\) para \(A_1\), e assim por diante.
Mas, aqui, a seta que corresponde a \(w_{10}\) não é mostrada. Alguns livros representariam este peso como uma seta que vem “do nada” para o nó \(A_1\). Outros livros representariam este peso como um valor dentro do nó \(A_1\).
Este peso \(w_{10}\), que não multiplica nenhum dos dados de entrada, é chamado de viés (bias, em inglês).
O resultado desta combinação linear é enviado para uma função \(g\), fazendo, então, com que a saída do nó \(A_1\) seja
\[ A_1 = g\;(w_{10} + w_{11} X_1 + w_{12} X_2 + w_{13} X_3 + w_{14} X_4) \]
ou, usando notação de somatório, mais compacta,
\[ A_1 = g\left( w_{10} + \sum_{j=1}^4 w_{1j} X_j\right) \]
A função \(g\) é chamada de função de ativação, e costuma ser uma função não-linear. Mais adiante, vamos ver exemplos específicos de funções de ativação.
Se a função \(g\) fosse linear, a rede neural seria equivalente a regressão linear, que é um modelo menos poderoso.
Ou seja, é a não-linearidade da função de ativação que faz com que uma rede neural possa computar funções que modelos lineares não são capazes de computar.

Os outros nós da camada oculta, \(A_2\) a \(A_5\), computam funções parecidas com a função computada pelo nó \(A_1\), mas com outros pesos.
Ou seja, no geral, para cada nó \(A_i\),
\[ \begin{aligned} A_i &= g\;(w_{i0} + w_{i1} X_1 + w_{i2} X_2 + w_{i3} X_3 + w_{i4} X_4) \\ &= g\left( w_{i0} + \sum_{j=1}^4 w_{ij} X_j\right) \end{aligned} \]
A função de ativação \(g\) costuma ser a mesma para todos os nós de uma mesma camada.
Terminada a computação da camada oculta, os valores de saída de \(A_1\) a \(A_5\) são enviados para o (único) nó da última camada, que produz \(Y\), o valor de saída da rede:
\[ \begin{aligned} Y &= \beta_0 + \beta_1 A_1 + \beta_2 A_2 + \beta_3 A_3 + \beta_4 A_4 + \beta_5 A_5 \\ &= \beta_0 + \sum_{k=1}^5 \beta_k A_k \end{aligned} \]
Aqui, neste exemplo, \(Y\) é função linear das saídas dos nós da camada oculta, mas é comum que \(Y\) também seja resultado de uma função não-linear.

Resumindo, os valores dos nós são calculados da seguinte forma:
\[ \begin{aligned} A_i &= g\left(w_{i0} + \sum_{j=1}^4 w_{ij} X_j\right) \\ Y &= \beta_0 + \sum_{k=1}^5 \beta_k A_k \end{aligned} \]
Esta rede tem \(4\) entradas, uma camada oculta com \(5\) unidades e função de ativação \(g()\), uma camada de saída com uma unidade (com função de ativação linear), e, como pesos (ou parâmetros), o seguinte conjunto de valores:
- \(w_{ij},\, 1 \leq i \leq 5,\, 0 \leq j \leq 4\) (\(25\) parâmetros),
- \(\beta_k,\, 0 \leq k \leq 5\) (\(6\) parâmetros).
Esta rede tem, então, \(31\) parâmetros no total.

1.4 Exemplos de funções de ativação
Já vimos que a função de ativação costuma ser não-linear.
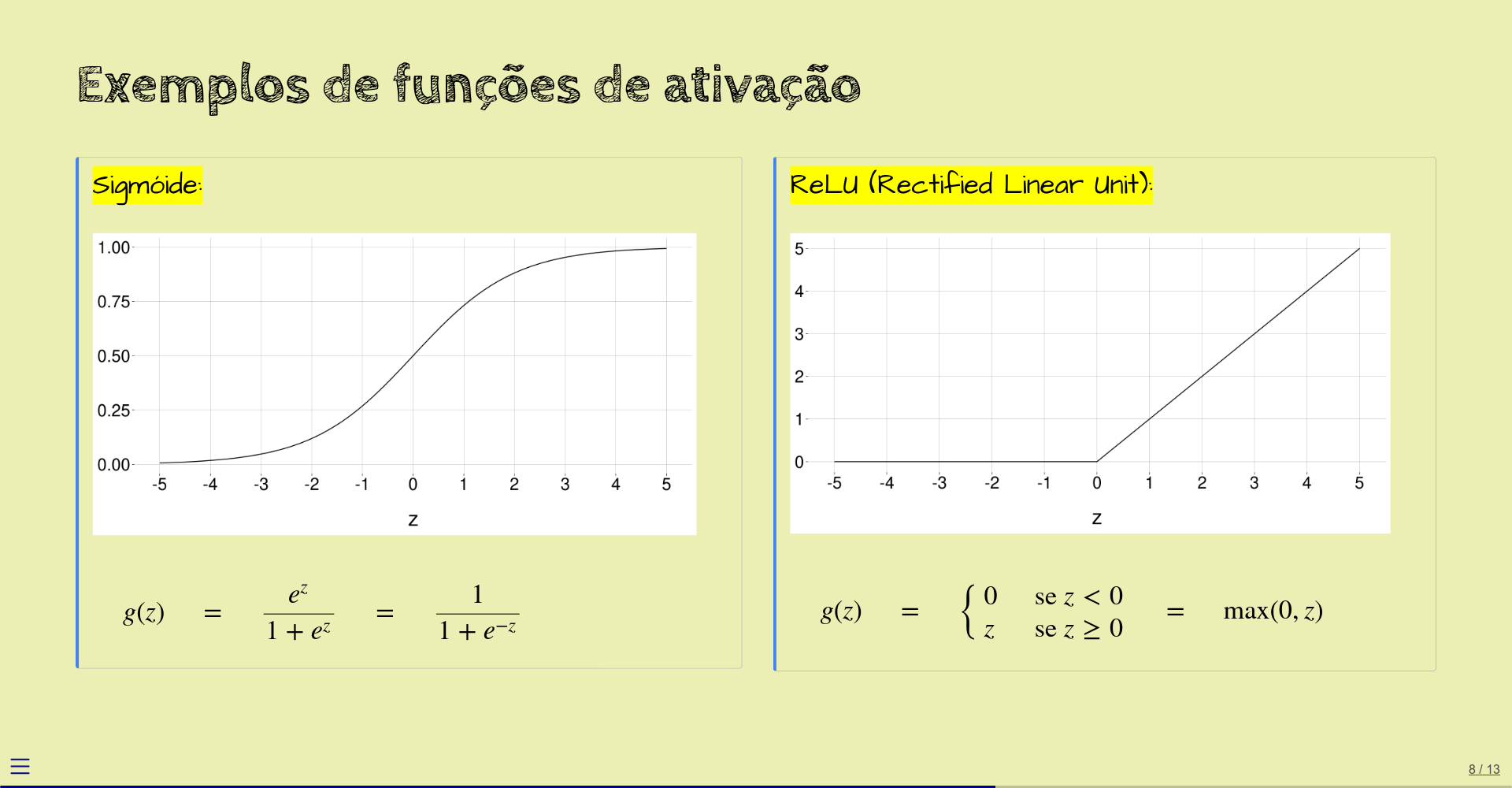
Um exemplo é a função sigmóide, que sempre retorna valores entre \(0\) e \(1\) (exclusive) e que tem o gráfico mostrado abaixo. Esta função “comprime”, por assim dizer, todos os números reais para o intervalo \((0, 1)\).
Historicamente, a função sigmóide foi uma das primeiras a ser usadas como função de ativação, mas atualmente damos preferência a outras, que são menos problemáticas. Mais adiante, vamos falar sobre isto.
A função sigmóide é útil, por exemplo, quando o nó precisa retornar uma probabilidade (que é um valor entre \(0\) e \(1\)).
Outro exemplo de função de ativação é a ReLU, bem mais simples de ser computada (e entendida). Se o argumento é negativo, a ReLU retorna zero; senão, retorna o próprio argumento. Atualmente, é uma das funções de ativação mais usadas em redes neurais.
Você pode achar que a ReLU, uma função que simplesmente zera os argumentos que estão abaixo de zero, é simples demais para aproximar funções lineares. Este exemplo mostra que não:
Vamos considerar a função quadrática \(f(x) = x^2 - 21x + 104\):
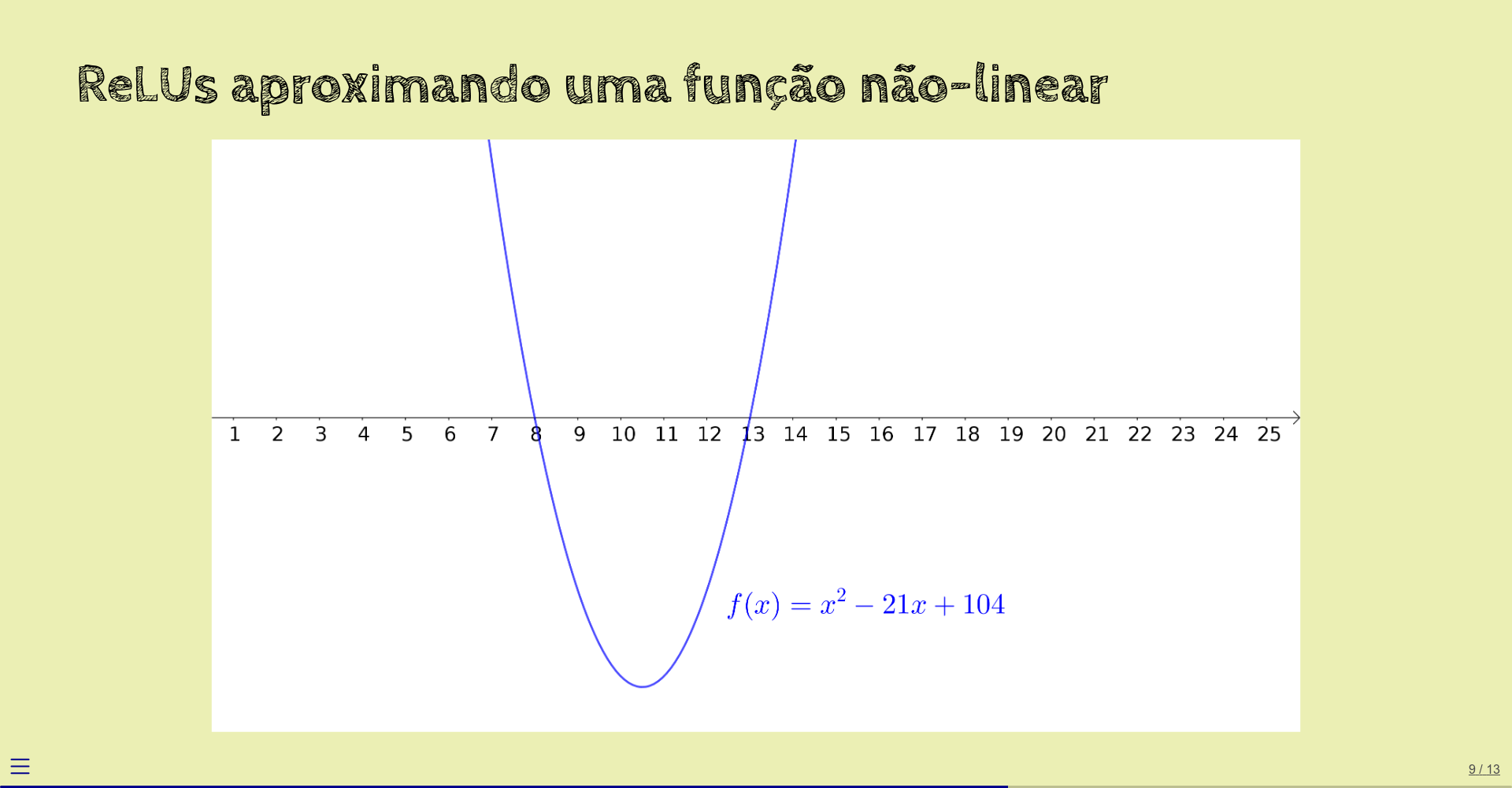
Começamos com uma função linear: \(f_1(x) = x/3 - 10/3\).
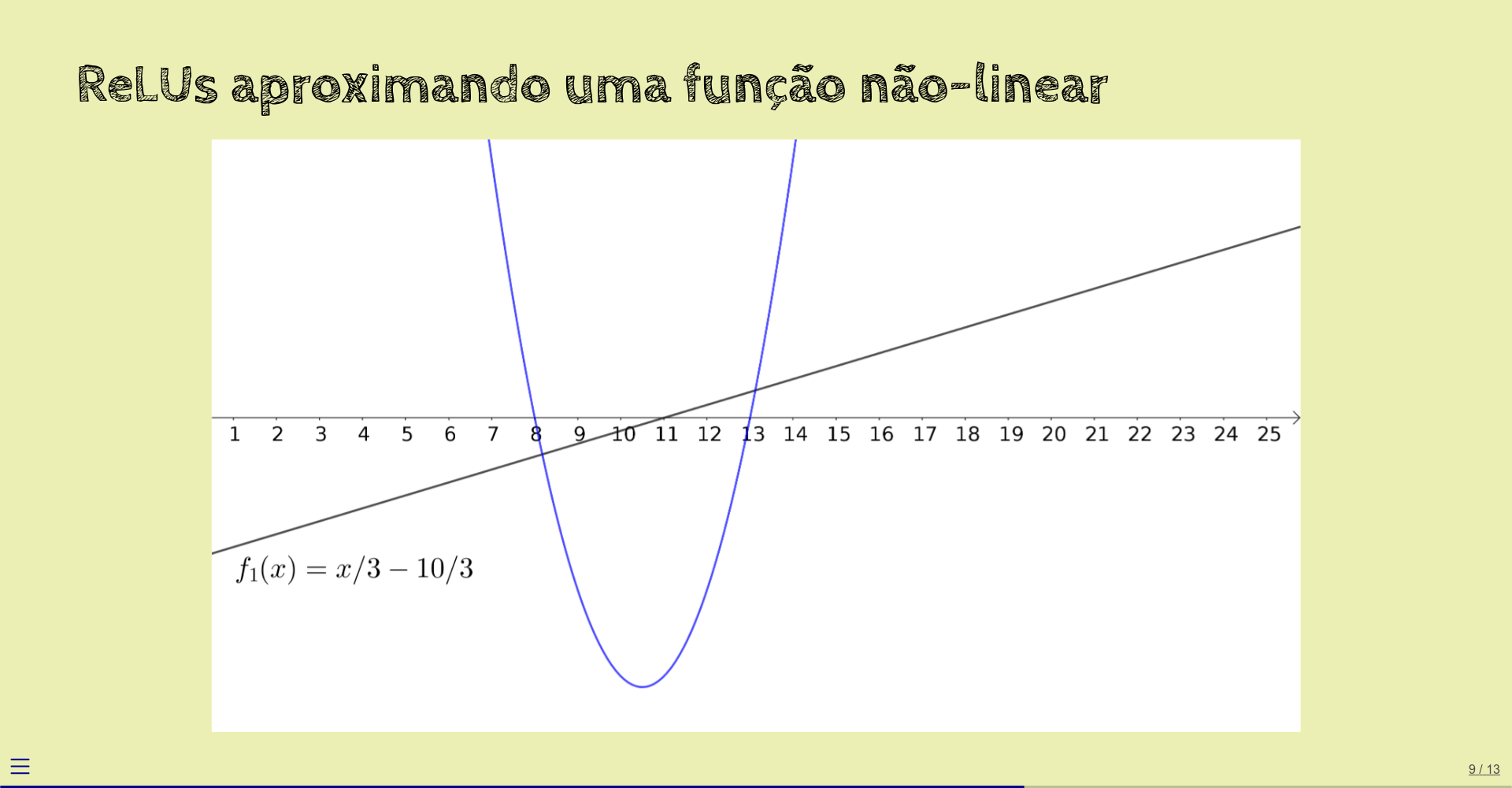
A seguir, aplicamos ReLU a esta reta:
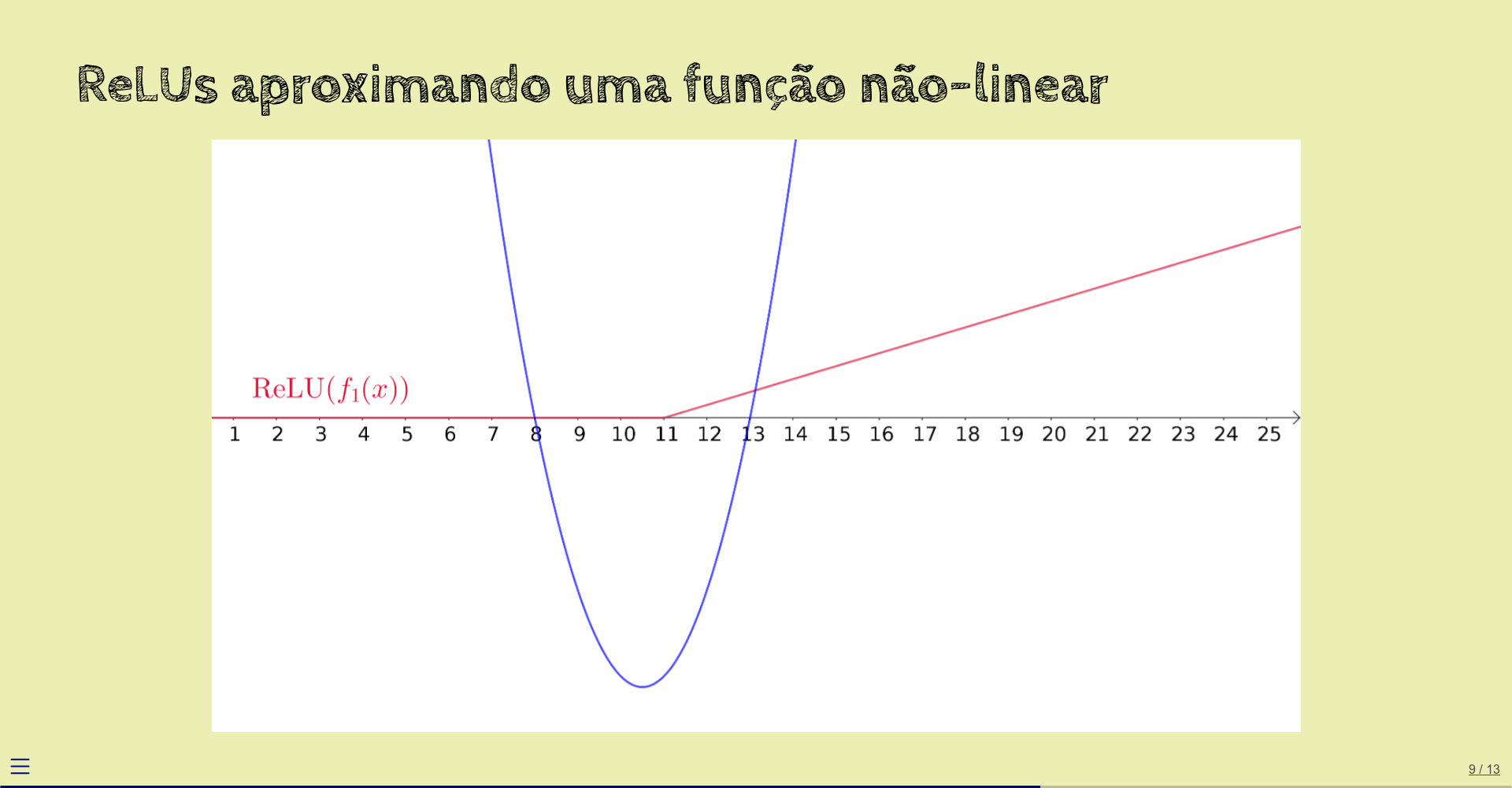
Agora, computamos outra função linear: \(f_2(x) = -x/3 + 3\).
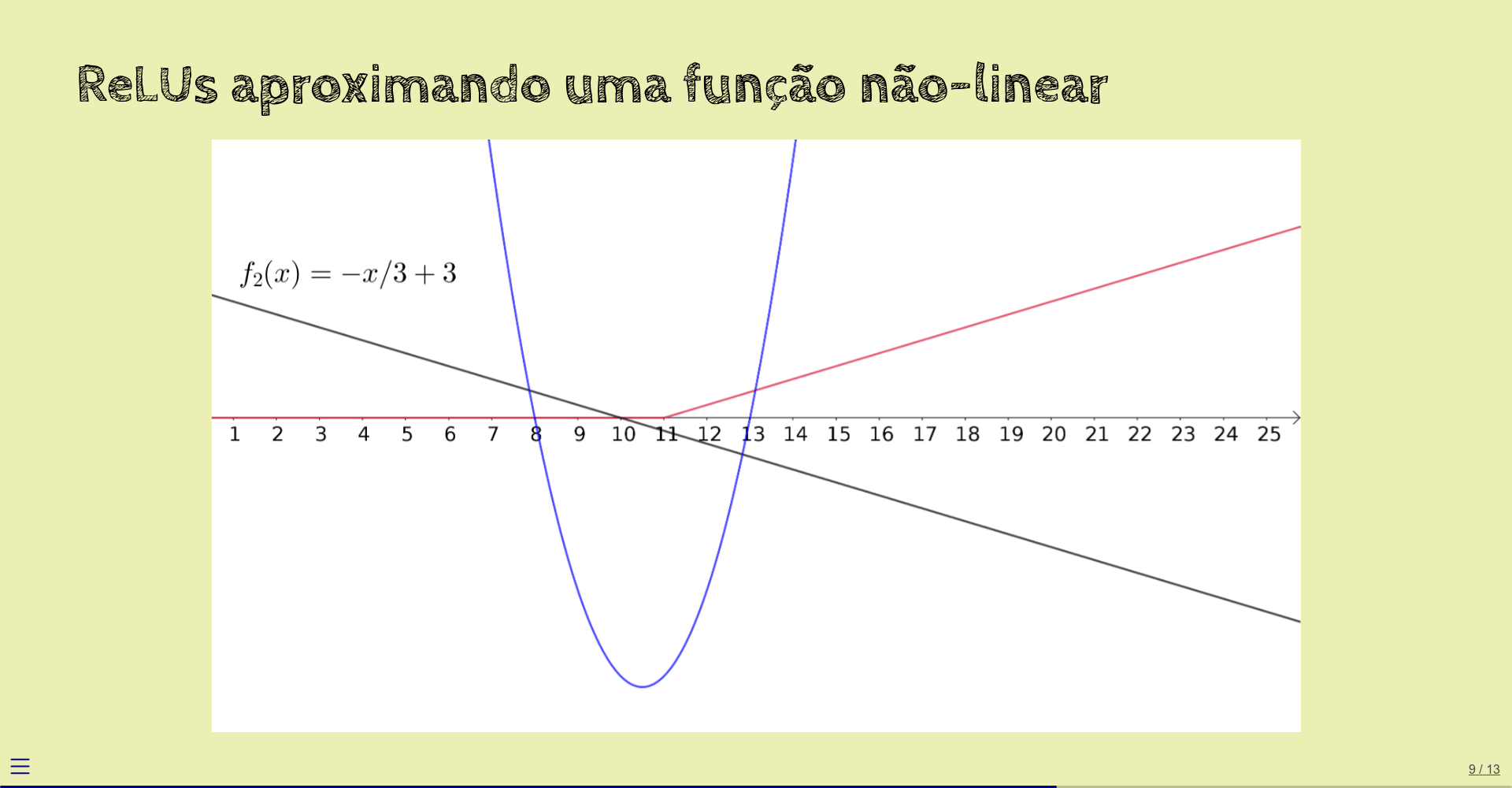
Aplicamos ReLU a esta reta também:
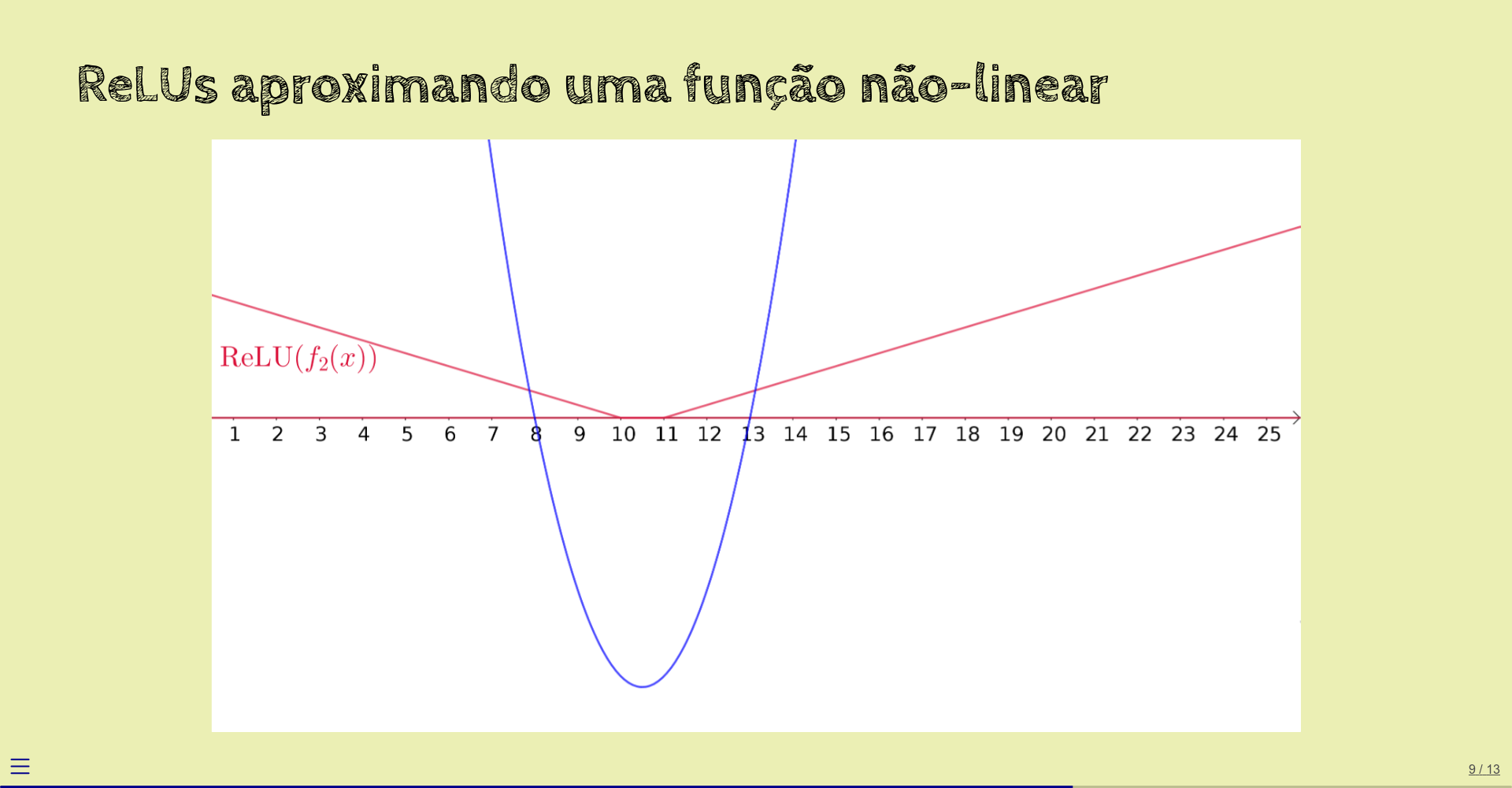
Somamos as duas ReLUs obtidas:
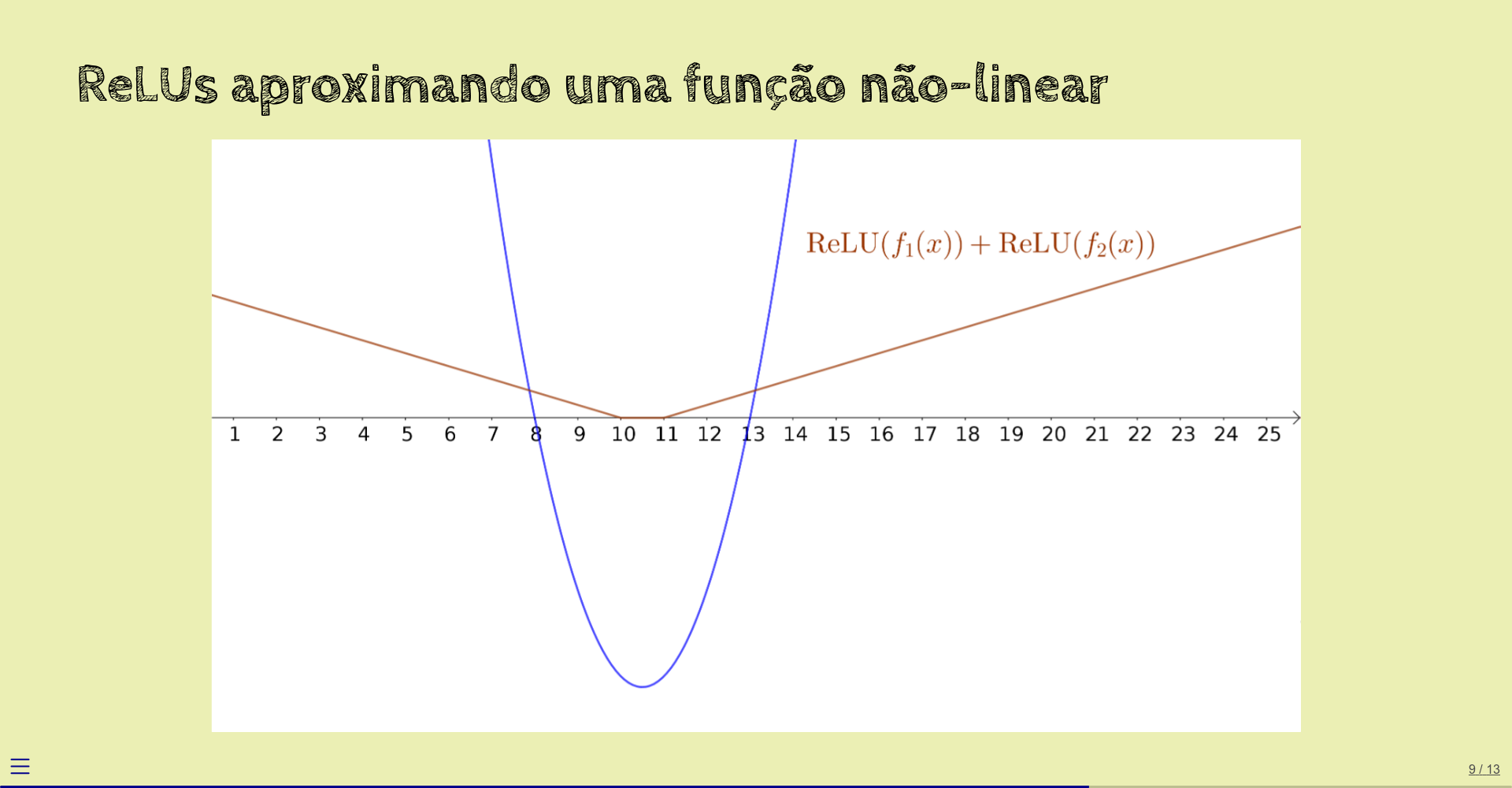
Não ficou muito próxima da função original.
Em vez de somar as duas ReLUs, vamos calcular uma combinação linear delas:
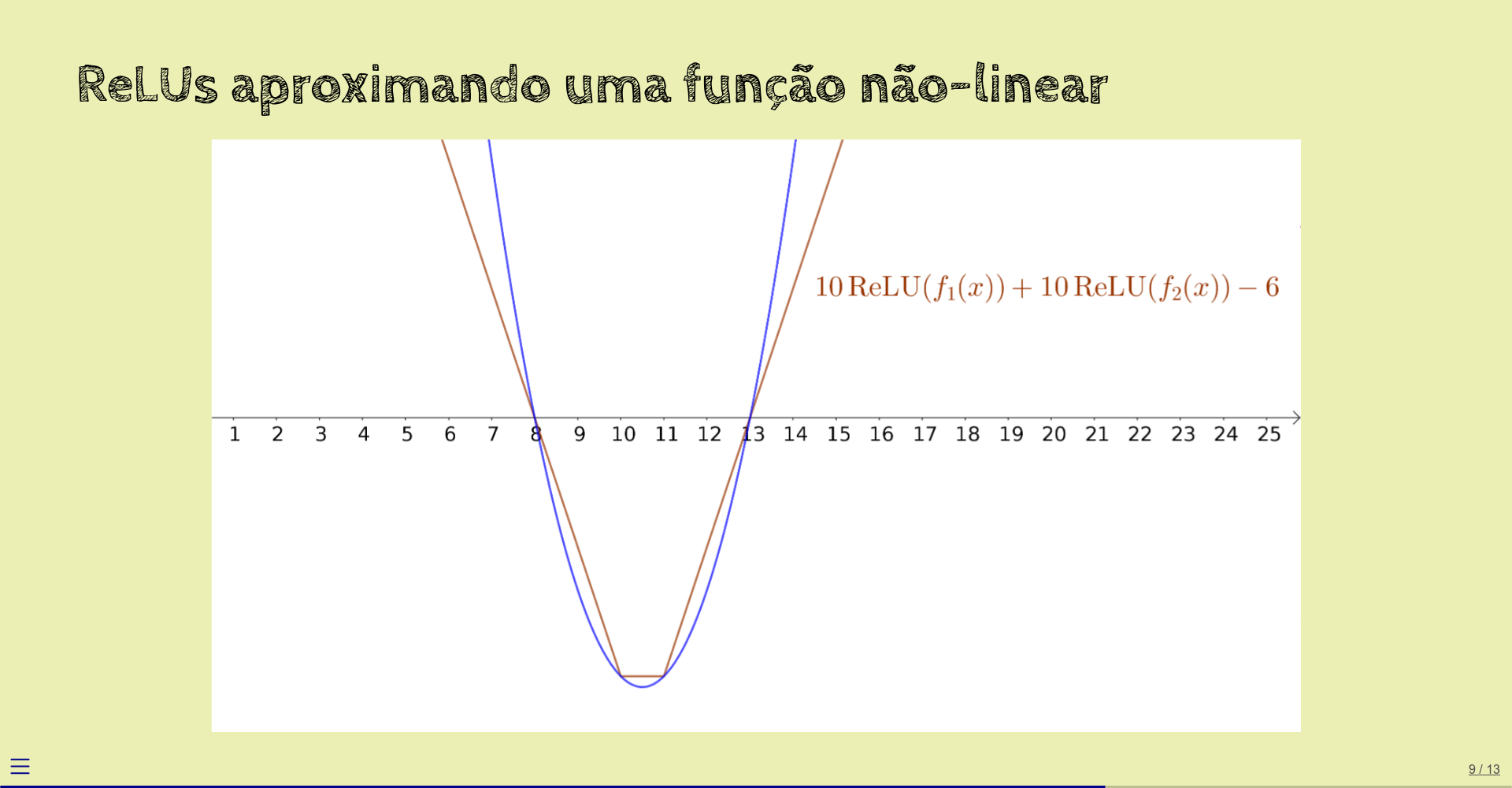
Agora, sim, o resultado aproxima a função \(f\) original.
Se usássemos mais funções lineares e aplicássemos mais ReLUs a elas, a aproximação seria melhor ainda.
1.5 Exemplo: aproximando uma função quadrática
Agora, vamos seguir esta mesma idéia, mas deixando uma rede neural fazer o trabalho.
Esta é uma rede neural com uma entrada \(x\), uma única camada oculta, com \(200\) neurônios, com função de ativação ReLU, e camada de saída com um único neurônio.
Com os valores dos pesos definidos por um processo de treinamento que vamos abordar depois, esta rede é capaz de retornar, para diversos valores de \(x\) entre \(-50\) e \(50\), o valor de \(x^2\), com mostra o gráfico:
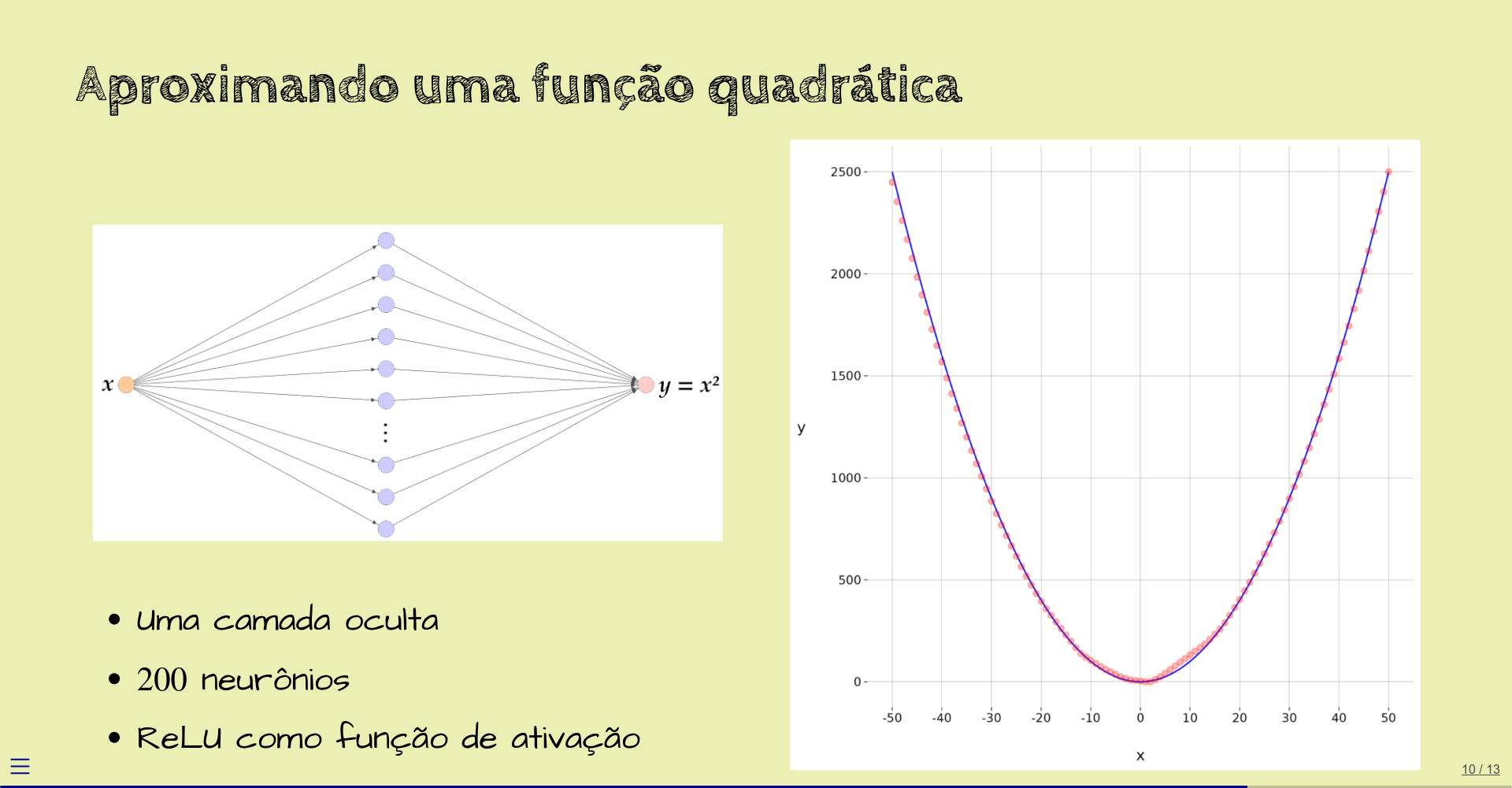
1.6 Regressão versus classificação
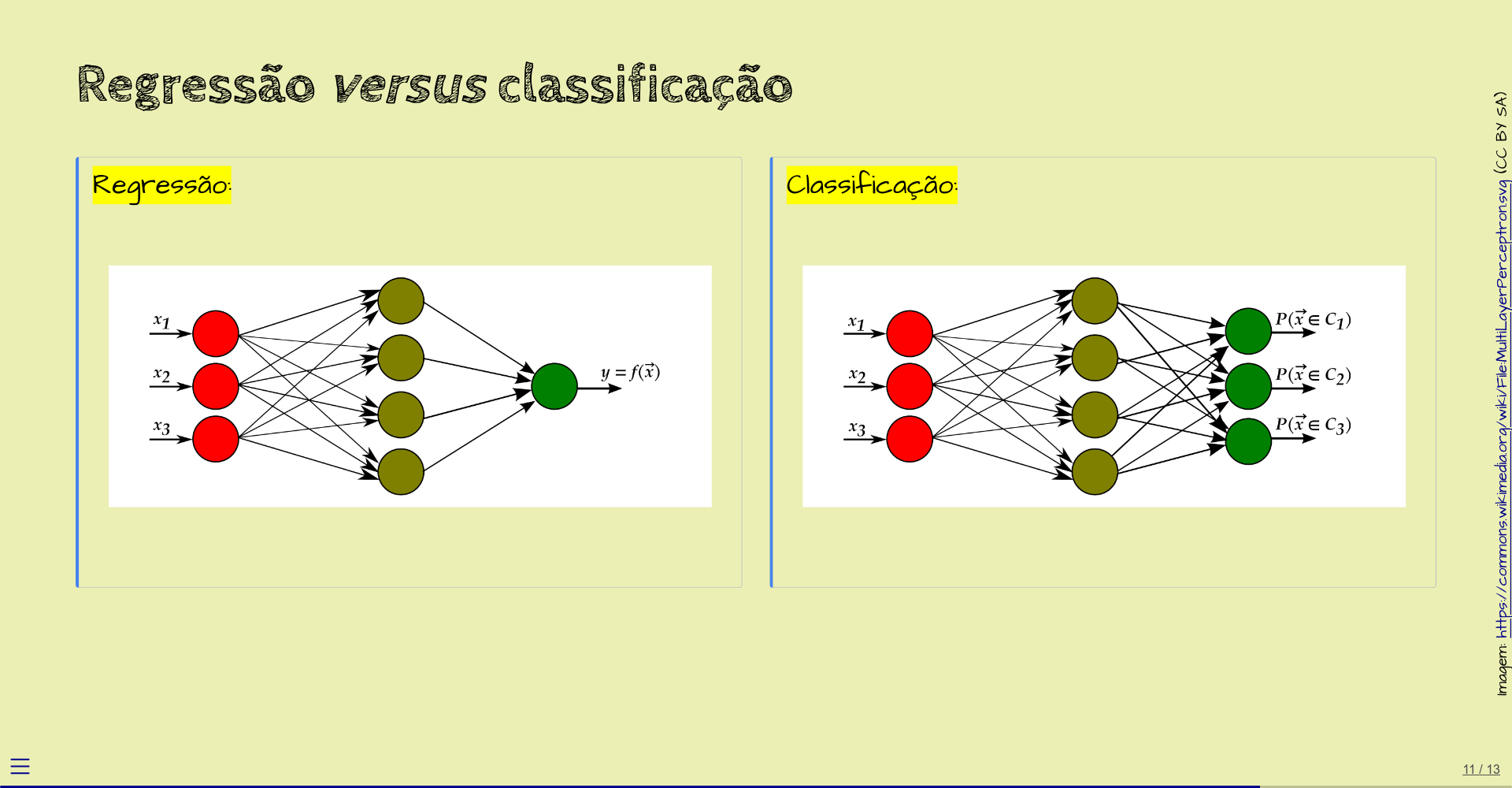
Os exemplos que vimos até agora são de redes neurais que calculam uma função numérica das variáveis de entrada. O que estas redes fazem é chamado de regressão.
Um outro tipo de rede neural serve para computar a qual classe pertencem os dados de entrada.
Por exemplo, as entradas podem representar dados numéricos sobre um paciente a ser diagnosticado, e as saídas (aqui, três) são as probabilidades de o paciente pertencer às classes
- \(C_1 = {}\) saudável,
- \(C_2 = {}\) indefinido,
- \(C_3 = {}\) doente.
Este tipo de rede faz o que chamamos de classificação.
Mais adiante, vamos ver outros exemplos.
1.7 O que falta ver?
A esta altura, você deve ter entendido o que é e para que serve uma rede neural.
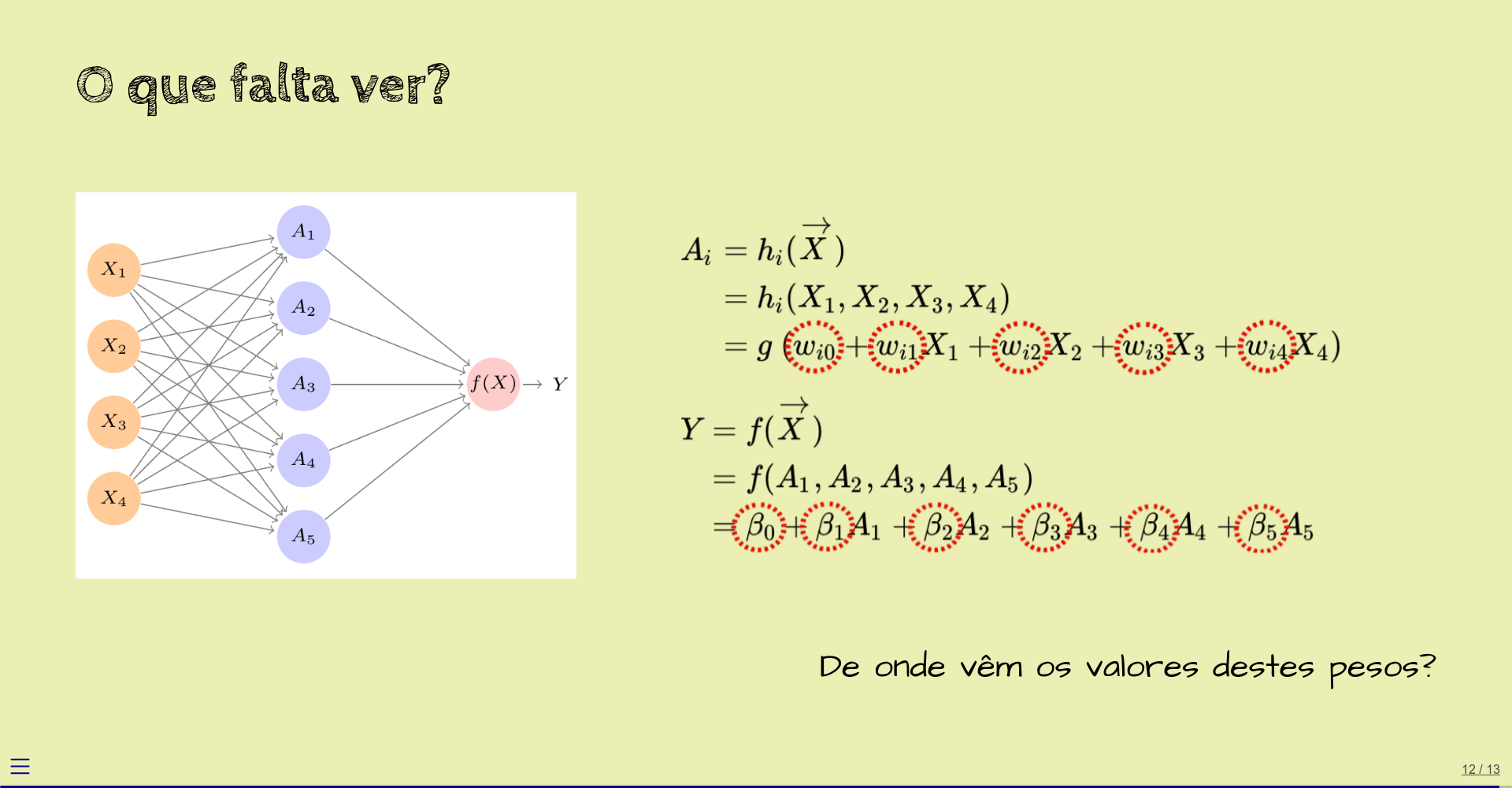
Os exemplos que vimos foram de redes “já prontas”, com os valores dos pesos já definidos para as tarefas que as redes deviam executar.
Uma pergunta importante, que não abordamos aqui, é a de como os valores destes pesos são escolhidos.
Em um outro capítulo, então, vamos falar sobre o processo de treinamento de uma rede neural, que é o que define os valores dos pesos.
1.8 Exercícios
No diagrama do nosso primeiro exemplo de rede neural, escreva, próximo a cada seta, o nome do peso correspondente:
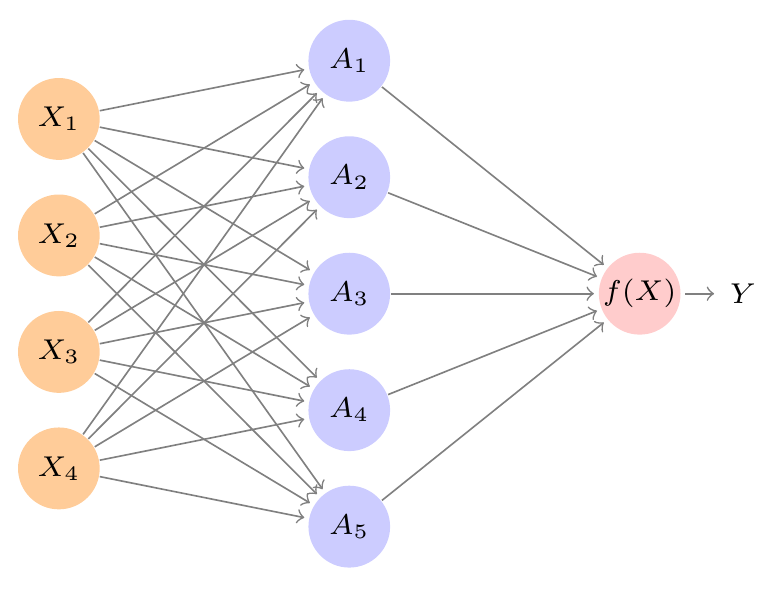
Lembre-se das equações:
\(A_i = g\;(w_{i0} + w_{i1} X_1 + w_{i2} X_2 + w_{i3} X_3 + w_{i4} X_4)\)
\(Y = \beta_0 + \beta_1 A_1 + \beta_2 A_2 + \beta_3 A_3 + \beta_4 A_4 + \beta_5 A_5\)
Como você decidiu representar os pesos \(w_{i0}\) e o peso \(\beta_0\) (os chamados vieses ou biases)?