04: Probabilidade condicional

Vídeo

Exercícios do livro (cap. 2)

2. Gêmeos

Uma mulher está grávida de meninos gêmeos.
Gêmeos podem ser idênticos ou fraternos.
\(1/3\) dos gêmeos são idênticos.
Gêmeos idênticos têm \(50\%\) de chance de serem ambos meninos, e \(50\%\) de chance de serem ambos meninas.
Para gêmeos fraternos, cada gêmeo tem, independentemente, \(50\%\) de chance de ser menino, e \(50\%\) de chance de ser menina.
Qual a probabilidade de a mulher estar grávida de gêmeos idênticos?

Eventos:

\[ \begin{aligned} I &= \text{os gêmeos são idênticos} \\ M &= \text{os gêmeos são dois meninos} \end{aligned} \]
Probabilidades dadas:

\[ \begin{aligned} P(I) &= 1/3 \\ P(M \mid I) &= 1/2 \\ P(M \mid \neg I) &= 1/4 \end{aligned} \]
Queremos calcular \(P(I \mid M)\). Usamos Bayes:

\[ \begin{aligned} P(I \mid M) &= \frac{P(M \mid I) \cdot P(I)}{P(M)} \end{aligned} \]
Só falta o valor de \(P(M)\), que calculamos usando probabilidade total:

\[ \begin{aligned} P(M) &= P(M \mid I)P(I) + P(M \mid \neg I)P(\neg I) \\ &= 1/2 \cdot 1/3 + 1/4 \cdot 2/3 \\ &= 1/3 \end{aligned} \]
Concluímos

\[ \begin{aligned} P(I \mid M) &= \frac{P(M \mid I) \cdot P(I)}{P(M)} \\ &= \frac{1/2 \cdot 1/3}{1/3} \\ &= 1/2 \end{aligned} \]

4. Múltipla escolha

Um aluno está resolvendo uma questão de múltipla escolha com \(n\) opções.
\(K\) é o evento que corresponde a ele saber a resposta correta.
\(R\) é o evento que corresponde a ele acertar (sabendo ou chutando).
Se ele sabe a resposta, ele acerta.
Se ele não sabe, ele chuta uma opção ao acaso.
Considere \(P(K) = p\).

Ache \(P(K \mid R)\).

Vamos usar Bayes, supondo \(p = P(K) > 0\):

\[ \begin{aligned} P(K \mid R) &= \frac{P(R \mid K) \cdot P(K)}{P(R)} \\ &= \frac{1 \cdot p}{ P(R \mid K) \cdot P(K) + P(R \mid \neg K) \cdot P(\neg K) } \\ &= \frac{p}{ 1 \cdot p + \frac{1}{n} \cdot (1 - p) } \\ &= \frac{np}{np + (1 - p)} \end{aligned} \]

Mostre que \(P(K \mid R) \geq p\). Por que isto faz sentido? Quando a igualdade é exata?

Isto equivale a mostrar

\[ \frac{np}{np + (1 - p)} \geq p \] Como todos os valores são positivos, isto equivale a

\[ np \geq np^2 + (1 - p)p \] Dividindo ambos os lados por \(p > 0\):

\[ n \geq np + 1 - p \]

Daí,

\[ \begin{aligned} n \geq np + 1 - p &\iff n - np \geq 1 - p \\ &\iff n(1 - p) \geq 1 - p \\ &\iff n \geq 1 & \text{(supondo } p < 1 \text{)} \end{aligned} \] O que é verdade, pois existe pelo menos uma opção (a correta).

Se \(p = 1\), a igualdade vale, e \(P(K \mid R) = 1\), pois o aluno sempre sabe a esposta e sempre acerta.

Se \(n = 1\), a igualdade vale, e \(P(K \mid R) = p\), pois o aluno acertar (ele empre acerta!) e o aluno saber são independentes.

Imagine \(n > 1\).

Lembre-se de que \(P(K \mid R) = \frac{P(K \cap R)}{P(R)}\).

O numerador é a probabilidade do evento “o aluno sabe e o aluno acerta”. Esta robabilidade é exatamente \(p\), pois “o aluno sabe” é sub-evento de “o aluno certa”.

O numerador \(P(R)\) é um número tal que \(0 < P(R) < 1\). Vamos chamar este úmero de \(1/x\), para \(x > 1\).

Então,

\[ P(K \mid R) = \frac{P(K \cap R)}{P(R)} = \frac{p}{1/x} = xp > p \]

Em R

Valores teóricos:

n <- 1:9
p <- seq(0, 1, .25)

df <- expand.grid(n = n, p = p) %>% 
  mutate(
    pkr_teorico = n * p / (p * (n - 1) + 1)
  ) %>% 
  arrange(n)

df

Gráfico:

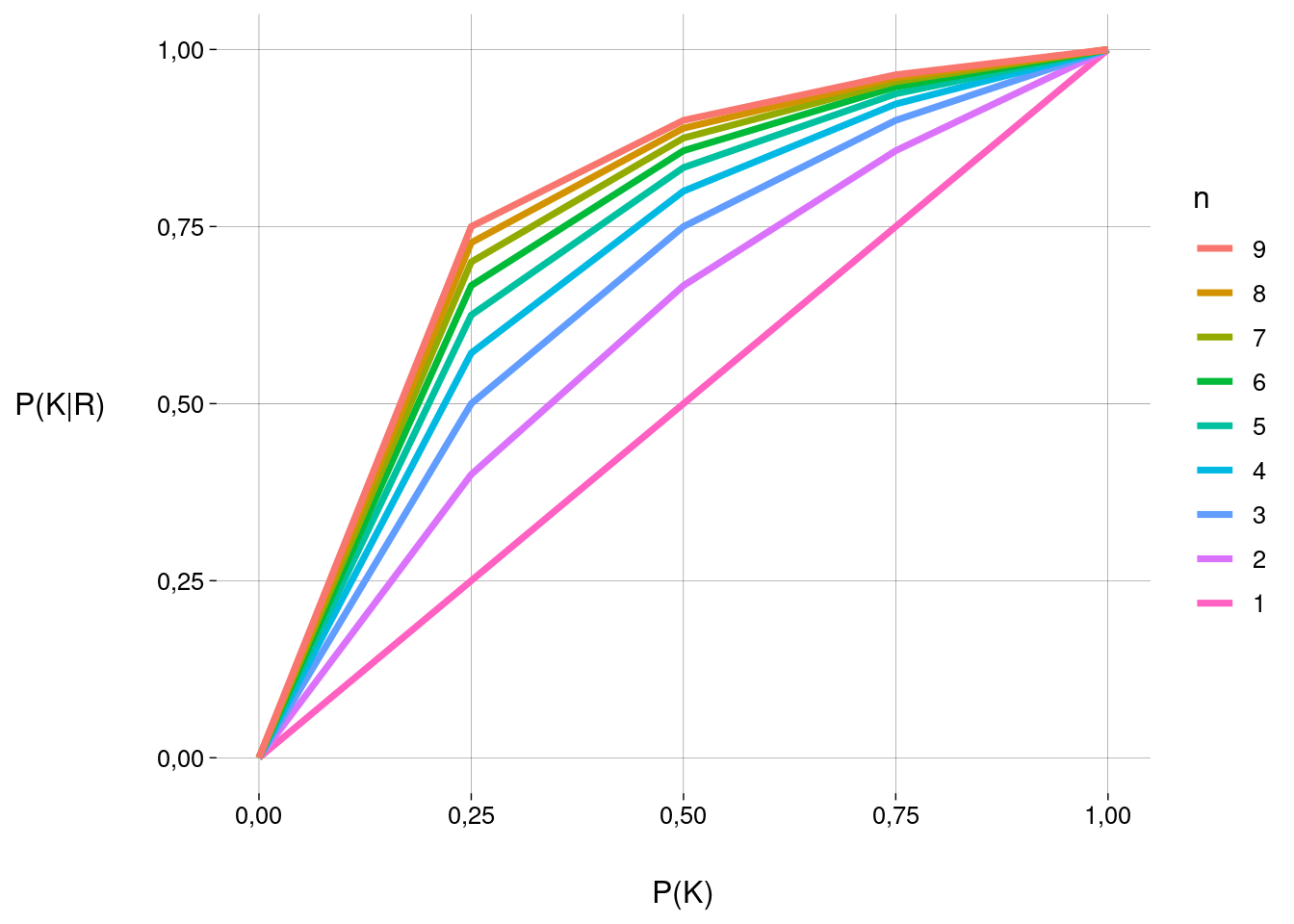
Conclusão óbvia: quanto maior o número \(n\) de opções, maior a probabilidade \(P(K \mid R)\) de o aluno ter acertado sabendo, em oposição a ter acertado chutando:

\[ \begin{aligned} \lim_{n \to \infty} P(K \mid R) &= \lim_{n \to \infty} \frac{np}{np + 1 - p} \\ &= \lim_{n \to \infty} \frac{p}{p} \\ &= 1 \end{aligned} \]

Simulação:

sim <- function(n, p, reps = 1e7) {
  
  sabe <- sample(
    c(TRUE, FALSE), 
    reps,
    replace = TRUE,
    c(p, 1 - p)
  )

  acerta <- sabe
  nao_sabe <- sum(!sabe)
  
  acerta[which(!sabe)] <- 
    sample(
      c(TRUE, FALSE),
      nao_sabe,
      replace = TRUE,
      prob = c(1/n, 1 - 1/n)
    )
  
  sum(sabe) / sum(acerta)
  
}

sim <- Vectorize(sim)

df <- df %>% 
  mutate(
    pkr_simulado = sim(n, p)
  )

df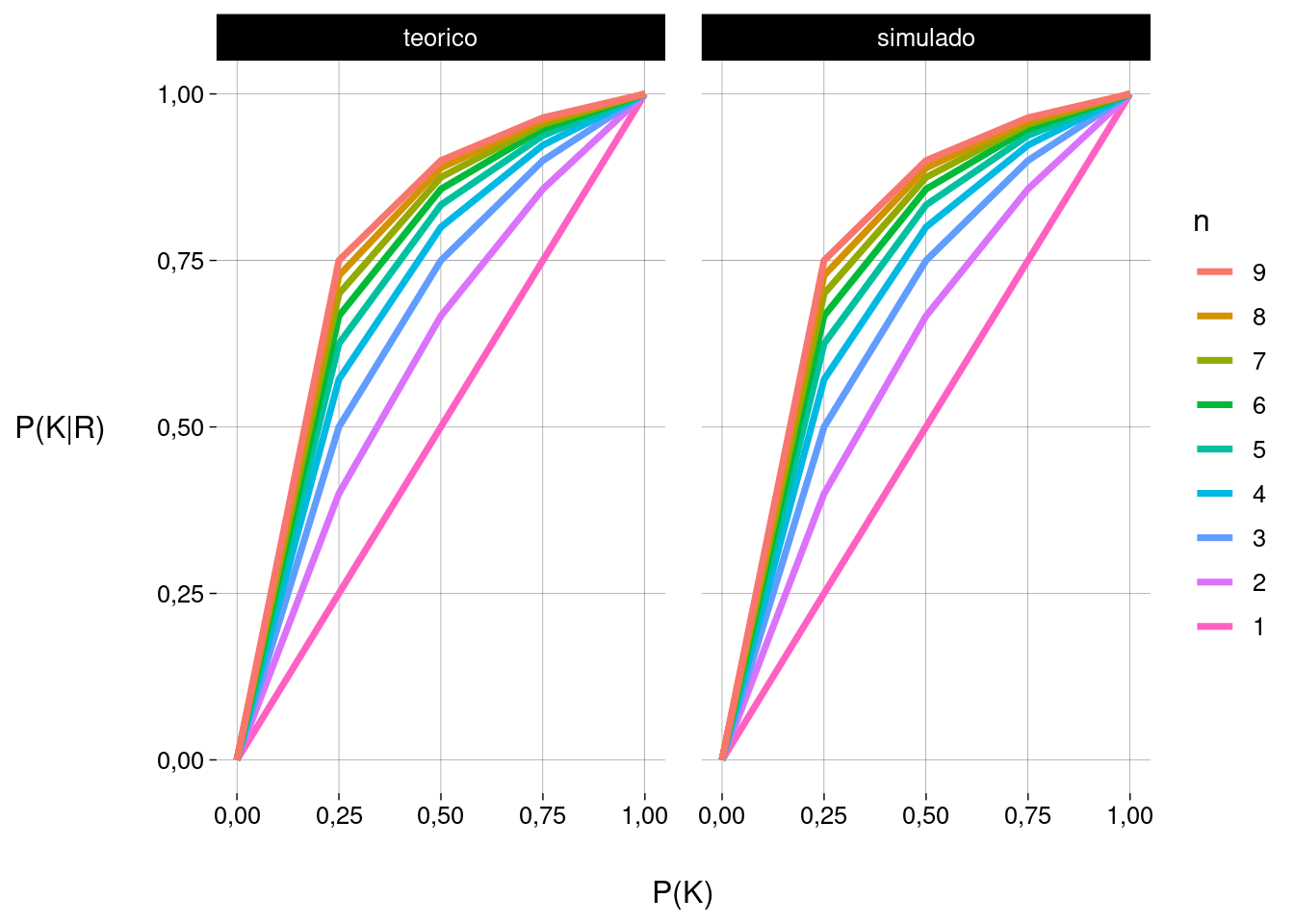

12. Mensagens em binário

Alice está tentando enviar uma mensagem codificada em binário para Bob.
- Ela envia um bit: \(0\) ou \(1\) com probabilidades iguais.
- Se ela envia \(0\), há probabilidade \(5\%\) de erro.
- Se ela envia \(1\), há probabilidade \(10\%\) de erro.
- Dado que Bob recebeu \(1\), qual a probabilidade de Alice ter enviado \(1\)?

Eventos e probabilidades:

Queremos achar \(P(A \mid B)\). Usando Bayes:

p0 <- .05
p1 <- .1
q0 <- 1 - p0
q1 <- 1 - p1

pA <- 1/2
pBIA <- q1
pB <- (q1 + p0) / 2
pAIB <- pBIA * pA / pB

pAIB

## [1] 0,9473684

Para sermos completos, vamos calcular outras probabilidades, com \(P(A) = P(\neg A) = 1/2\):

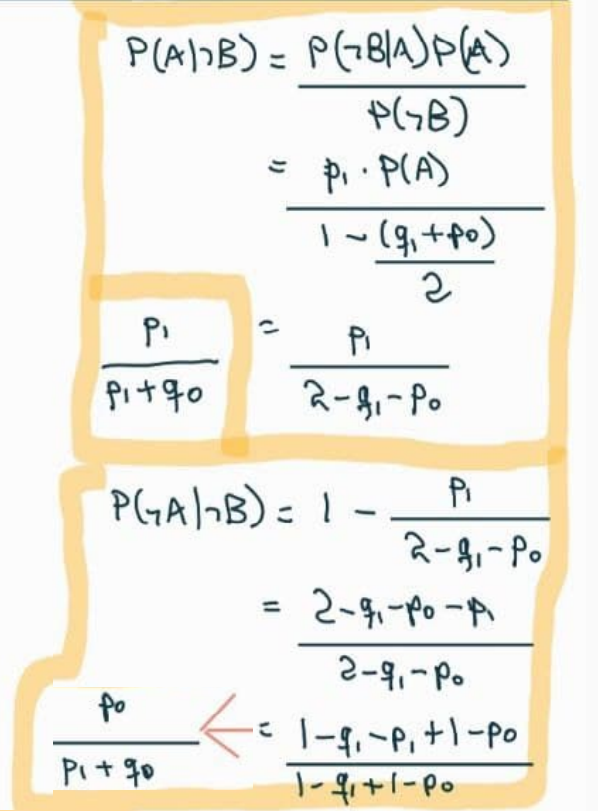
Simulação:

reps <- 1e7
alice_envia <- sample(c(0, 1), reps, replace = TRUE)
bob_recebe <- alice_envia

bob_recebe[which(alice_envia == 0)] <- 
  sample(
    c(0, 1), 
    length(which(alice_envia == 0)),
    replace = TRUE,
    prob = c(95/100, 5/100)
  )

bob_recebe[which(alice_envia == 1)] <- 
  sample(
    c(0, 1), 
    length(which(alice_envia == 1)),
    replace = TRUE,
    # Atenção: aqui, erro é 1 virar 0:
    prob = c(10/100, 90/100)  
  )

pab <- sum(alice_envia & bob_recebe) / sum(bob_recebe)
pab

## [1] 0,947354

Agora, eles usam um código com repetição:
- Alice envia \(000\) para representar \(0\) e \(111\) para representar \(1\).
- Bob decodifica a mensagem tomando o bit que está em maioria.
- As probabilidades de erro são como antes, e os erros em bits diferentes são independentes.
- Dado que Bob recebe \(110\), qual a probabilidade de que Alice tenha enviado \(111\)?

Eventos:

\[ \begin{aligned} AAA &= \text{Alice envia } 111 \\ BB\neg B &= \text{Bob recebe } 110 \end{aligned} \]
\(P(AAA) = 1/2\), pois Alice envia somente \(111\) ou \(000\).
Usando Bayes:

\[ P(AAA \mid BB\neg B) = \frac{P(BB\neg B \mid AAA) \cdot P(AAA)}{P(BB\neg B)} \]
\(P(BB\neg B \mid AAA) = q_1 \cdot q_1 \cdot p_1\), pois erros em bits diferentes são independentes.
Pela lei da probabilidade total:

\[ \begin{aligned} P(BB\neg B) &= P(BB\neg B \mid AAA) \cdot P(AAA) + P(BB\neg B \mid \neg(AAA))P(\neg(AAA)) \\ &= \frac12 \cdot \left( q_1 \cdot q_1 \cdot p_1 + p_0 \cdot p_0 \cdot q_0 \right) \end{aligned} \]
Daí,

\[ \begin{aligned} P(AAA \mid BB\neg B) &= \frac{P(BB\neg B \mid AAA) \cdot P(AAA)}{P(BB\neg B)} \\ &= \frac{ q_1 \cdot q_1 \cdot p_1 \cdot 1/2 }{ \left( q_1 \cdot q_1 \cdot p_1 + p_0 \cdot p_0 \cdot q_0 \right)\cdot 1/2 } \\ &= \frac{ q_1 \cdot q_1 \cdot p_1 }{ \left( q_1 \cdot q_1 \cdot p_1 + p_0 \cdot p_0 \cdot q_0 \right) } \end{aligned} \]

Numericamente:

q1 * q1 * p1 / (q1 * q1 * p1 + p0 * p0 * q0)

## [1] 0,9715142

14. Probabilidades condicionais e complementos

Se \(P(A), P(B) \in (0, 1)\), então

\[ P(A \mid B) > P(A \mid \neg B) \iff P(B \mid A) > P(B \mid \neg A) \]

???

15. Torcer para qual evento?

\(A\) e \(B\) são eventos com

\[ 0 < P(A \cap B) < P(A) < P(B) < P(A \cup B) < 1 \]

Você está torcendo para que \(A\) e \(B\) ambos ocorram.

O que você ficaria mais feliz em observar?

Que \(A\) ocorreu?
Que \(B\) ocorreu?
Que \(A \cup B\) ocorreu?

Queremos observar o evento \(E\) tal que \(P(A \cap B \mid E)\) seja máximo.

\[ \begin{aligned} P(A \cap B \mid A) &= \frac{P(A \cap B)}{P(A)} \\ P(A \cap B \mid B) &= \frac{P(A \cap B)}{P(B)} \\ P(A \cap B \mid A \cup B) &= \frac{P((A \cap B) \cap (A \cup B))}{P(A \cup B)} \\ &= \frac{P(A \cap B)}{P(A \cup B)} \end{aligned} \]
Como \(P(A)\) é o menor denominador, observar \(A\) maximiza \(P(A \cap B \mid E)\).
Intuitivamente, como \(A\) é o evento menos provável dos dois, saber que \(A\) ocorreu nos deixa mais próximo da ocorrência dos dois eventos do que saber que \(B\) (ou que algum dos dois) ocorreu.

16. Ajudar e atrapalhar

\[ P(A \mid B) \leq P(A) \implies P(A \mid \neg B) \geq P(A) \]

Se a ocorrência de \(B\) torna \(A\) menos provável, então a não-ocorrência de \(B\) torna \(A\) mais provável.
Pela lei da probabilidade total:

\[ \begin{aligned} P(A) &= P(A \mid B)P(B) + P(A \mid \neg B)P(\neg B) \\ \therefore P(A \mid \neg B) &= \frac{P(A) - P(A \mid B)P(B)}{P(\neg B)} \end{aligned} \]
Daí,

\[ \begin{aligned} P(A \mid \neg B) &\geq \frac{P(A) - P(A)P(B)}{P(\neg B)} & \text{pois } P(A \mid B) \leq P(A) \\ &= \frac{P(A)(1 - P(B))}{P(\neg B)} \\ &= P(A) \end{aligned} \]

17. Contrapositiva

Em lógica determinística, \(A \to B \iff \neg B \to \neg A\).

Em probabilidades?

Considere eventos \(A\) e \(B\) com \(P(A), P(B) \not\in \{0, 1\}\).

Mostre que \(P(B \mid A) = 1 \implies P(\neg A \mid \neg B) = 1\).

\(A\) está contido em \(B\):

\[ P(B \mid A) = 1 \iff \frac{P(A \cap B)}{P(A)} = 1 \iff P(A \cap B) = P(A) \]
Vamos mostrar que \(P(\neg A \mid \neg B) = 1\):

\[ \begin{aligned} P(\neg A \mid \neg B) &= \frac{P(\neg A \cap \neg B)}{P(\neg B)} \\ &= \frac{P(\neg (A \cup B))}{P(\neg B)} \\ &= \frac{1 - P(A \cup B)}{P(\neg B)} \\ &= \frac{1 - \left[ P(A) + P(B) - P(A \cap B) \right]}{P(\neg B)} \\ &= \frac{1 - P(B)}{P(\neg B)} \\ &= \frac{P(\neg B)}{P(\neg B)} \\ &= 1 \end{aligned} \]

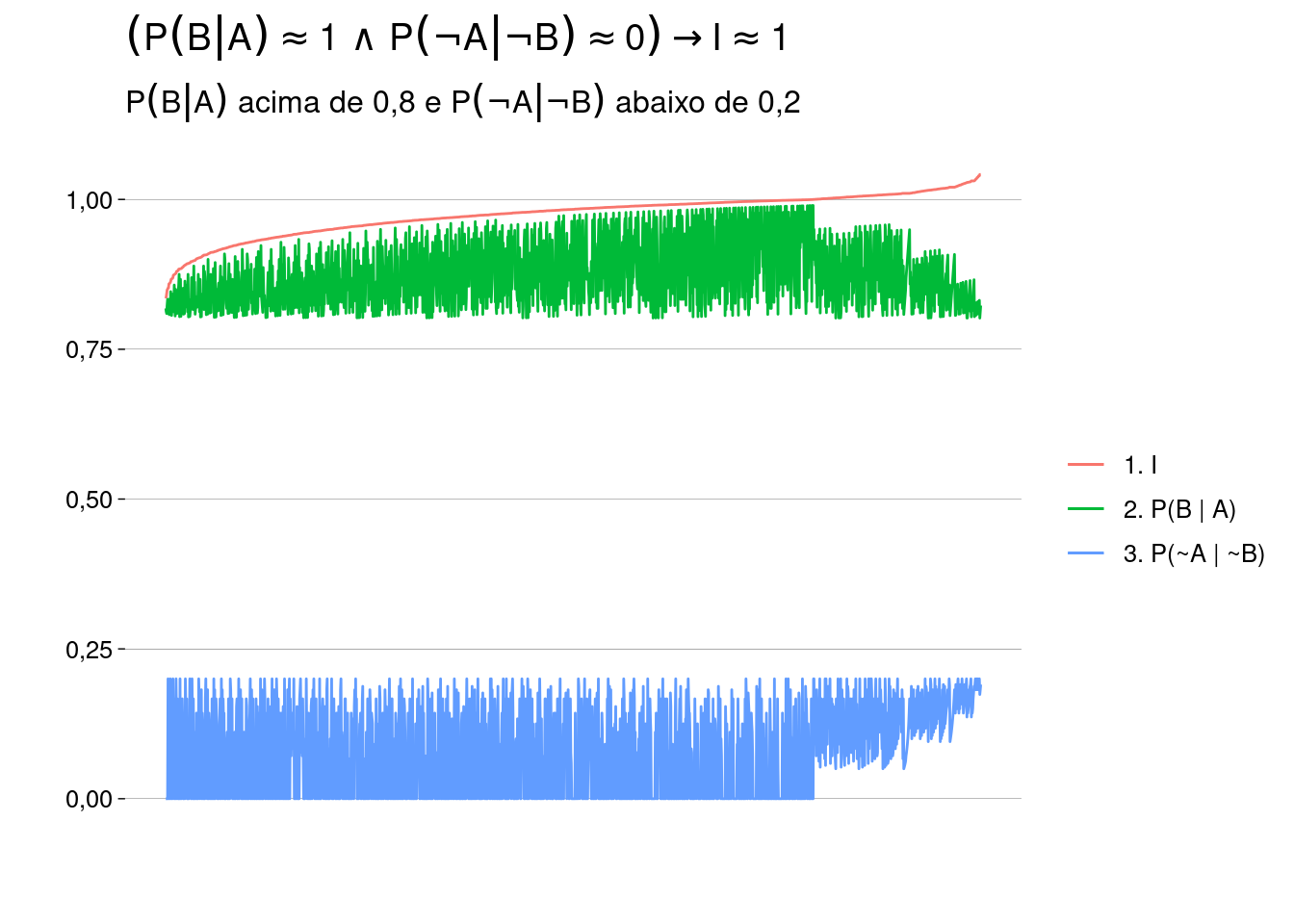
Mostre que, se “\(=\)” for substituído por “\(\approx\)”, o resultado não vale. Ache um exemplo em que \(P(B \mid A)\) seja quase \(1\), mas \(P(\neg A \mid \neg B)\) seja quase \(0\).

Valores de exemplo, com \(A\) e \(B\) independentes:

\[ \begin{aligned} P(A) &= 80/100 \\ P(B) &= 90/100 \\ P(\neg A) &= 20/100 \\ P(\neg B) &= 10/100 \\ P(A \cap B) &= P(A) \cdot P(B) = 72/100 \\ P(A \cup B) &= P(A) + P(B) - P(A \cap B) = 98/100\\ P(B \mid A) &= \frac{P(A \cap B)}{P(A)} = 72/80 \approx 1 \\ P(\neg A \mid \neg B) &= \frac{P(\neg A \cap \neg B)}{P(\neg B)} = \frac{1 - P(A \cup B)}{P(\neg B)} = 2/10 \approx 0 \end{aligned} \]

Vamos criar uma medida de independência. Se \(P(A) \neq 0\) e \(P(B) \neq 0\), definimos

\[ I = \frac{P(A \cap B)}{P(A)P(B)} \]

Com isso,

\(A\) e \(B\) são disjuntos \({} \iff I = 0\)
\(A\) e \(B\) são independentes \({} \iff I = 1\)
\(A\) e \(B\) se atrapalham \({} \iff 0 < I < 1\).

I.e., \(P(A) > P(A \mid B)\) e \(P(B) > P(B \mid A)\).
\(A\) e \(B\) se ajudam \({} \iff I > 1\).

I.e., \(P(A) < P(A \mid B)\) e \(P(B) < P(B \mid A)\).

22. Lewis Carroll

Este problema foi proposto pela primeira vez por Lewis Carroll em 1893.

Uma bolsa contém uma bola, que é ou azul, ou verde, com probabilidades iguais.
Uma bola verde é colocada na bolsa; agora, há \(2\) bolas na bolsa.
Uma bola é retirada da bolsa ao acaso.
A bola retirada é verde.
Qual é a probabilidade de que a bola que sobrou na bolsa seja verde?

Antes de mais nada, vamos definir os eventos:

\[ \begin{aligned} O &= \text{bola original é verde} \\ R &= \text{bola retirada é verde} \\ S &= \text{bola que sobrou é verde} \end{aligned} \]
O importante é perceber que o enunciado diz que o evento \(R\) aconteceu, mas as probabilidades devem ser calculadas pensando em todos os resultados possíveis, antes de o experimento acontecer.
Ou seja, em vez de tomar \(P(R) = 1\) — o que seria errado — vamos calcular \(P(S \mid R)\): a probabilidade de que a bola que sobrou seja verde, sabendo que a bola retirada foi verde.
Começamos com a lei da probabilidade total, condicionando aos dois casos possíveis:

\[ \begin{aligned} P(S \mid R) &= \underbrace{P(S \mid R, O) \cdot P(O \mid R)}_{\text{caso 1: bola original verde}} \;+\; \underbrace{P(S \mid R, \neg O) \cdot P(\neg O \mid R)}_{\text{caso 2: bola original azul}} \end{aligned} \]
No caso \(1\):

\[ \begin{aligned} P(S \mid R, O) \cdot P(O \mid R) &= 1 \cdot P(O \mid R) \\ &= P(O \mid R) \end{aligned} \]
No caso \(2\):

\[ \begin{aligned} P(S \mid R, \neg O) \cdot P(\neg O \mid R) &= 0 \cdot P(\neg O \mid R) \\ &= 0 \end{aligned} \]

Isto faz sentido: se a bola original era azul, não há como a bola que sobrou ser verde.
Só precisamos calcular a probabilidade do caso \(1\), que é \(P(O \mid R)\). Vamos usar Bayes:

\[ \begin{aligned} P(O \mid R) &= \frac{P(R \mid O) \cdot P(O)}{P(R)} \\ &= \frac{1 \cdot 1/2}{P(R)} \end{aligned} \]
Para calcular \(P(R)\), lei da probabilidade total de novo, condicionando sobre a bola original:

\[ \begin{aligned} P(R) &= P(R \mid O) \cdot P(O) + P(R \mid \neg O) \cdot P(\neg O) \\ &= 1 \cdot 1/2 + 1/2 \cdot 1/2 \\ &= 3/4 \end{aligned} \]
Chegamos a

\[ \begin{aligned} P(O \mid R) &= \frac{P(R \mid O) \cdot P(O)}{P(R)} \\ &= \frac{1 \cdot 1/2}{P(R)} \\ &= \frac{1/2}{3/4} \\ &= \frac{2}{3} \end{aligned} \]
Outra maneira de calcular \(P(S \mid R)\) seria aplicar Bayes primeiro:

\[ P(S \mid R) = \frac{P(R \mid S) \cdot P(S)}{P(R)} \]

mas as probabilidades do numerador são mais difíceis de calcular! Teríamos que usar a lei da probabilidade total duas vezes para o numerador (além de uma vez para o denominador).

29. Características menos e mais específicas

Uma família tem \(2\) crias.

Cada cria tem a mesma probabilidade de ser menino ou menina, e os sexos delas são independentes.

Cada cria tem a característica \(C\) com probabilidade \(p\), independentemente uma da outra e do sexo.

Mostre que a probabilidade de serem duas meninas, dado que pelo menos uma das crias é uma menina com a característica \(C\), é

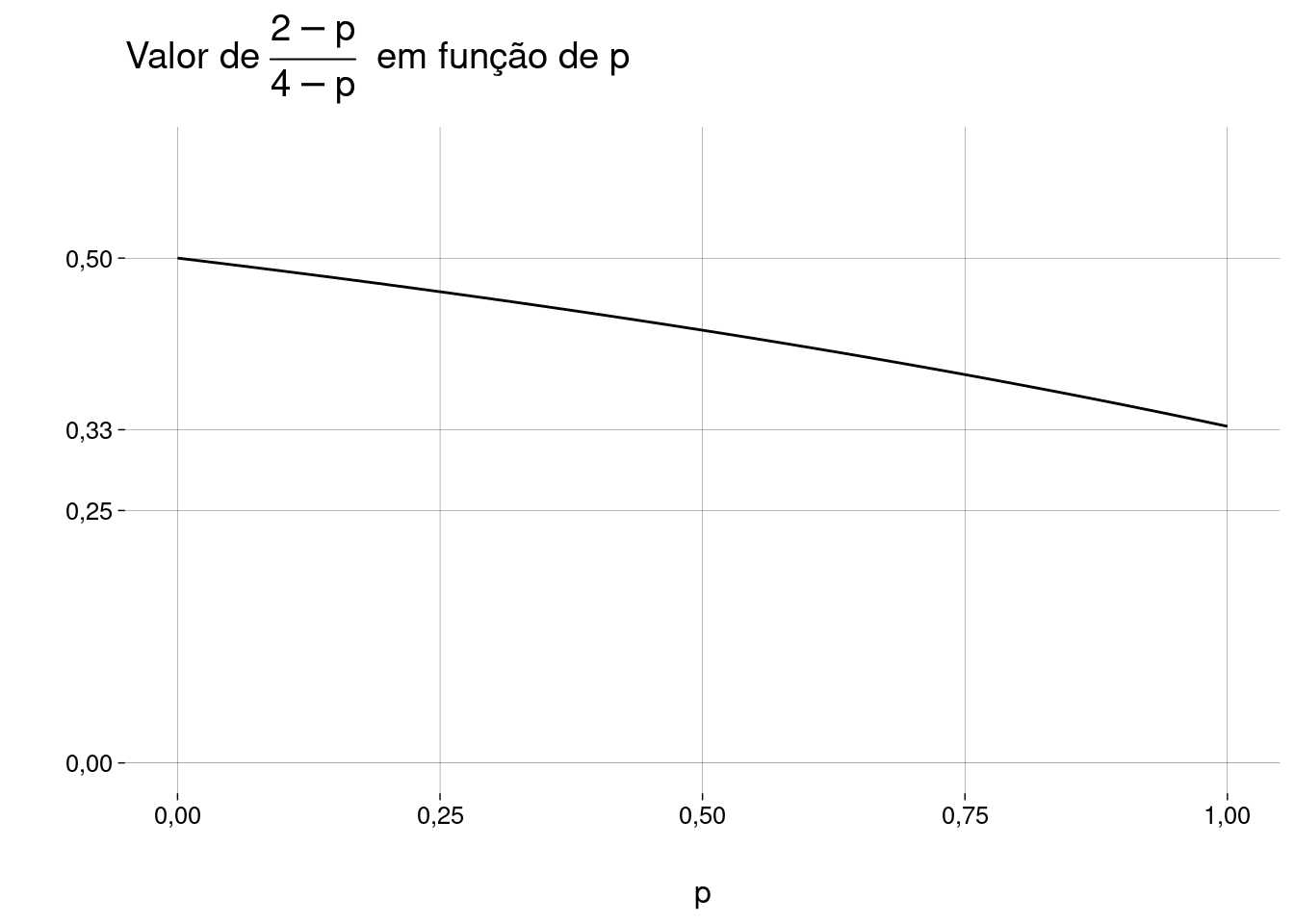
\[ \frac{2 - p}{4 - p} \]

Observe:

Se \(p = 1\), então a probabilidade é \(1/3\), como no exemplo 2.2.5.
Se \(p \to 0\), então a probabilidade tende a \(1/2\) pela esquerda, como no exemplo 2.2.7.

Eventos:

\[ \begin{aligned} AA &= \text{As duas são meninas} \\ AC &= \text{Pelo menos uma é menina e tem } C \end{aligned} \]
Vamos usar Bayes:

\[ P(AA \mid AC) = \frac{P(AC \mid AA) \cdot P(AA)}{P(AC)} \]
A probabilidade de ambas serem meninas é

\[ P(AA) = 1/4 \]
A probabilidade \(P(AC)\) de pelo menos uma ser menina e ter \(C\) é a soma das probabilidades de
- Ambas serem meninas, ambas terem \(C\): \(\frac14 \cdot p^2\).
- Ambas serem meninas, só uma ter \(C\) (a primeira ou a segunda): \(2 \cdot \frac14 \cdot p \cdot (1 - p)\).
- Uma ser menina com \(C\), a outra ser menino (com ou sem \(C\)): \(\frac12 \cdot p\).
- Logo, \[ P(AC) = \frac{p \cdot (4 - p)}{4} \]
A probabilidade \(P(AC \mid AA)\) de uma ser menina com \(C\), dado que ambas são meninas, é

\[ \begin{aligned} P(AC \mid AA) &= 1 - (1 - p)^2 \\ &= p \cdot (2 - p) \end{aligned} \]
Juntando tudo:

\[ \begin{aligned} P(AA \mid AC) &= \frac{P(AC \mid AA) P(AA)}{P(AC)} \\ &= \frac {p \cdot (2 - p) \cdot 1/4} {p \cdot (4 - p) \cdot 1/4} \\ &= \frac{2 - p}{4 - p} \end{aligned} \]
Um gráfico:

03: Problema do aniversário, propriedades

05: Probabilidade condicional (continuação)