2  Regressão linear múltipla

2.1 Simulação

Multicolinearidade

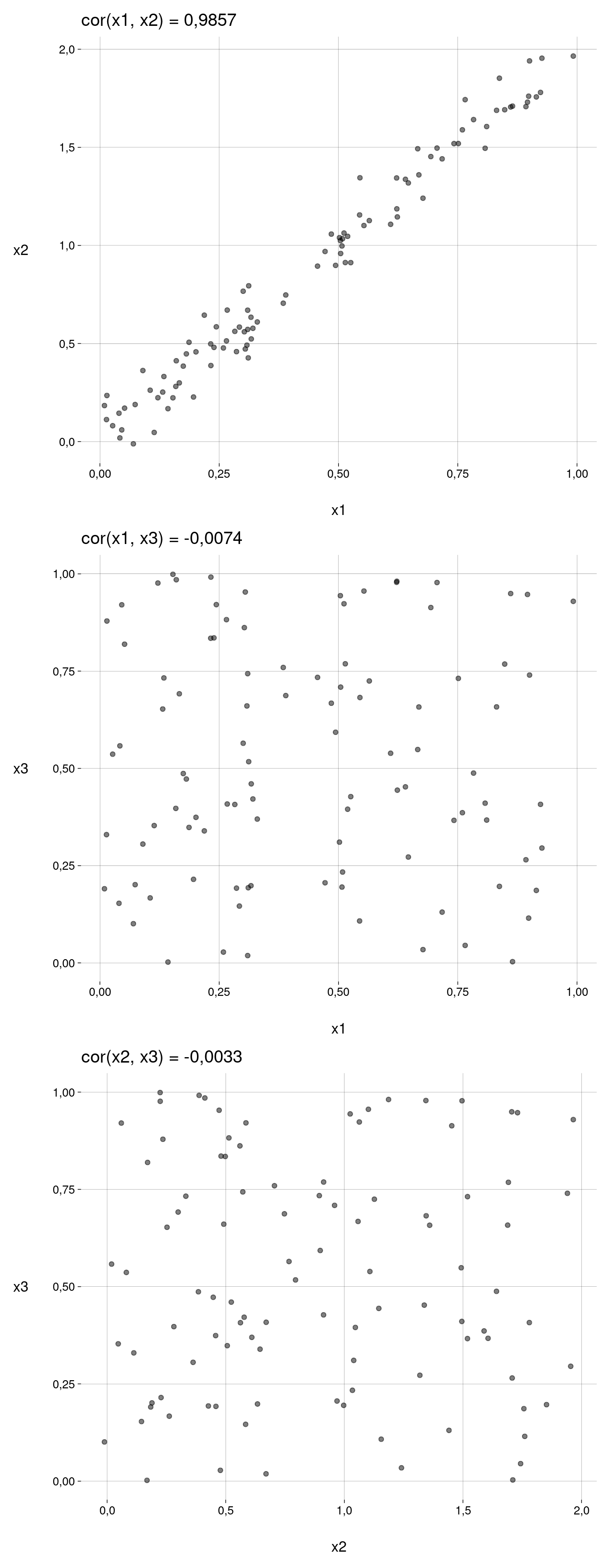
Vamos criar três preditores x1, x2 e x3, com os dois primeiros correlacionados:

n <- 100
a <- 2
x1 <- runif(n)
x2 <- a * x1 + rnorm(n, 0, .1)
x3 <- runif(n)

df <- tibble(x1, x2, x3)

Gráficos:

plot_cor <- function(df, v1, v2) {
  
  x = df[[v1]]
  y = df[[v2]]
  valor_cor <- cor(x, y) %>% round(4)
  
  df %>% ggplot(aes(x, y)) +
    geom_point(alpha = 0.5) +
    labs(
      title = paste0('cor(', v1, ', ', v2, ') = ', valor_cor),
      x = v1,
      y = v2
    )
  
}

v <- c('x1', 'x2', 'x3')

pares <- expand_grid(x = v, y = v) %>% 
  filter(x < y) %>% 
  arrange(x, y)

v1 <- pares %>% pull(x)
v2 <- pares %>% pull(y)

plots <- map2(
  v1, v2, ~ plot_cor(df, .x, .y)
)

plots %>% 
  wrap_plots(
    ncol = 1,
    byrow = TRUE
  )

A variável de resposta é y:

b0 <- 1
b1 <- 2
b2 <- 3
b3 <- 4
var_epsilon <- .5

y <- b0 + b1 * x1 + b2 * x2 + b3 * x3 + rnorm(n, sd = sqrt(var_epsilon))
df_y <- df %>% 
  mutate(y = y)

Usando todas as variáveis, temos:

modelo_123 <- lm(y ~ ., data = df_y)

A equação verdadeira é

\[ y = 1 + 2 x_1 + 3 x_2 + 4 x_3 + \varepsilon \]

O modelo deu os coeficientes

modelo_123 %>% summary()

Call:
lm(formula = y ~ ., data = df_y)

Residuals:
     Min       1Q   Median       3Q      Max 
-2,39333 -0,42820  0,08625  0,38997  1,83332 

Coefficients:
            Estimate Std. Error t value             Pr(>|t|)    
(Intercept)   1,2345     0,1747   7,068       0,000000000252 ***
x1            3,2787     1,4582   2,249              0,02683 *  
x2            2,3932     0,7203   3,323              0,00126 ** 
x3            3,7137     0,2286  16,245 < 0,0000000000000002 ***
---
Signif. codes:  0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1

Residual standard error: 0,681 on 96 degrees of freedom
Multiple R-squared:  0,9334,    Adjusted R-squared:  0,9313 
F-statistic: 448,6 on 3 and 96 DF,  p-value: < 0,00000000000000022

modelo_123

Call:
lm(formula = y ~ ., data = df_y)

Coefficients:
(Intercept)           x1           x2           x3  
      1,235        3,279        2,393        3,714  

Agora, usando apenas x1 e x3:

modelo_13 <- lm(y ~ x1 + x3, data = df_y)

A equação verdadeira é — substituindo \(x_2\) por \((b_1 + ab_2)x_1\) —

\[ y = 1 + 8 x_1 + 4 x_3 + \varepsilon \]

O modelo deu os coeficientes

modelo_13 %>% summary()

Call:
lm(formula = y ~ x1 + x3, data = df_y)

Residuals:
    Min      1Q  Median      3Q     Max 
-2,2807 -0,4648  0,0890  0,4492  1,8246 

Coefficients:
            Estimate Std. Error t value             Pr(>|t|)    
(Intercept)   1,2489     0,1834   6,808       0,000000000825 ***
x1            8,0547     0,2580  31,224 < 0,0000000000000002 ***
x3            3,7315     0,2401  15,543 < 0,0000000000000002 ***
---
Signif. codes:  0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1

Residual standard error: 0,7153 on 97 degrees of freedom
Multiple R-squared:  0,9258,    Adjusted R-squared:  0,9242 
F-statistic: 604,7 on 2 and 97 DF,  p-value: < 0,00000000000000022

modelo_13

Call:
lm(formula = y ~ x1 + x3, data = df_y)

Coefficients:
(Intercept)           x1           x3  
      1,249        8,055        3,732  

Em termos do \(R^2\) ajustado:

• O modelo com os três preditores teve \(R^2_{\text{adj}} = 0{,}9313\).
• O modelo com dois preditores teve \(R^2_{\text{adj}} = 0{,}9242\).

Para a equação verdadeira:

y_eq <- b0 + b1 * x1 + b2 * x2 + b3 * x3
rsq_vec(y, y_eq)

[1] 0,931878

Anova diz que o segundo modelo é mais significativo que o primeiro:

anova(modelo_123, modelo_13)

modelo_123 %>% glance()

modelo_13 %>% glance()