Os valores achados são estimativas para \(\beta_0\) e \(\beta_1\), baseadas nos dados do conjunto de treino.
Por isso, os valores de vendas obtidos com esta equação também são estimativas.
Vamos escrever estimativas com o acento circunflexo (chapéu) sobre os símbolos.
De onde vêm os valores de \(\hat{\beta_0}\) e \(\hat{\beta_1}\)?
Resposta: são os valores que fazem com que a soma dos quadrados das distâncias verticais dos pontos à reta seja a menor possível.
(Estas distâncias são chamadas de resíduos.)
Consulte este material para ver os detalhes sobre o cálculo de \(\hat{\beta_0}\) e \(\hat{\beta_1}\).
Erros-padrão das estimativas
Vamos pensar nas incertezas associadas aos valores de \(\hat{\beta_0}\) e \(\hat{\beta_1}\), com base na excelente discussão em (De Veaux, Velleman e Bock 2016, cap. 25).
Quais são os fatores que afetam a nossa confiança na reta de regressão?
Mais especificamente, quais os fatores que afetam nossa confiança no valor estimado \(\hat\beta_1\) (a inclinação da reta)?
Espalhamento dos pontos em volta da reta
Quanto mais afastados da reta estiverem os dados, menor a nossa confiança de que a reta captura a variação de uma variável em função da outra.
Observe a Figura 1.1. O gráfico da esquerda nos dá mais certeza de que uma reta de regressão terá uma inclinação bem próxima da taxa de variação de \(y\) em função de \(x\) na população.
Figura 1.1: Espalhamento dos pontos
Este espalhamento é medido pelo desvio-padrão dos resíduos.
Pela Figura 1.1 e pelos comentários acima, quanto maior o valor de \(s_{\text{residuos}}\), maior a nossa incerteza.
Espalhamento de \(x\)
Quanto maior o espalhamento dos valores de \(x\), maior nossa confiança na reta de regressão, pois ela estará baseada em uma diversidade maior de valores.
Observe a Figura 1.2. O gráfico da direita tem um espalhamento maior dos valores de \(x\). Uma reta de regressão, ali, parece estar mais bem “ancorada”.
Figura 1.2: Espalhamento de \(x\)
O espalhamento de \(x\) é medido pelo desvio-padrão, que é calculado da maneira usual.
Nesta matriz, a segunda coluna corresponde à coluna x dos dados. A primeira coluna, com valores \(1\), está ali para podermos escrever o modelo como a equação matricial
As colunas x e y do conjunto de dados são vetores com \(3\) componentes, que vivem em \(\mathbb{R}^3\).
O vetor \(\mathbf{\widehat Y}\) também tem \(3\) componentes, mas a Equação 1.1 está dizendo que \(\mathbf{\widehat Y}\) é uma combinação linear dos dois vetores (linearmente independentes) \([1\ 1\ 1]^T\) e \([1\ 2\ 3]^T\).
Os dois vetores \([1\ 1\ 1]^T\) e \([1\ 2\ 3]^T\) não são capazes de gerar todo o espaço \(\mathbb{R}^3\); o espaço gerado por eles é um plano.
O vetor \(\mathbf{Y}\) (com os valores verdadeiros da variável de resposta \(y\)) não está no plano gerado pelos vetores \([1\ 1\ 1]^T\) e \([1\ 2\ 3]^T\) (verifique).
A relação verdadeira entre \(\mathbf{Y}\) e \(\mathbf{X}\) é
\[
\begin{bmatrix}
y_1 \\ {y_2} \\ {y_3}
\end{bmatrix}
=
\beta_0 \cdot
\begin{bmatrix}
1 \\ 1 \\ 1
\end{bmatrix}
+
\beta_1 \cdot
\begin{bmatrix}
1 \\ 2 \\ 3
\end{bmatrix}
+
\begin{bmatrix}
\varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3
\end{bmatrix}
\] onde os valores \(\varepsilon_i\) são os erros que o modelo não consegue capturar.
Estes erros \(\varepsilon_i\) são estimados pelos resíduos \(\widehat{\varepsilon_i}\), de maneira que podemos escrever
O plano cinza é o espaço gerado pelos vetores \([1\ 1\ 1]^T\) e \([1\ 2\ 3]^T\). Na equação paramétrica deste plano, \(r\) e \(s\) correspondem aos valores possíveis de \(\beta_0\) e \(\beta_1\), respectivamente.
O vetor \(\mathbf{\widehat{Y}}\) (dos valores previstos pelo modelo) é a projeção ortogonal do vetor \(\mathbf{Y}\) (dos valores verdadeiros da variável de resposta) sobre o plano gerado pelas colunas da matriz \(\mathbf{X}\). Mais abaixo, vamos ver os detalhes desta projeção. O importante é entender que, quaisquer que sejam os valores de \(\beta_0\) e \(\beta_1\), o vetor \(\mathbf{\widehat{Y}}\) de valores previstos vai estar sempre limitado ao plano gerado pelas colunas da matriz \(\mathbf{X}\).
Isto corresponde à intuição de que estamos perdendo informação ao tentar representar objetos de dimensão \(3\) (o número de observações do conjunto de dados) em um espaço de dimensão \(2\) (o número de parâmetros do modelo: \(\beta_0\) e \(\beta_1\)).
James, Gareth, Daniela Witten, Trevor Hastie, e Robert Tibshirani. 2021. An Introduction to Statistical Learning: With Applications in R. 2.ª ed. Springer Publishing Company, Incorporated. https://www.statlearning.com/.
{{< include _math.qmd >}}```{r echo=FALSE, message=FALSE}source('_setup.R')set.seed(1234)```# Regressão linear simples## Exemplo: vendas e publicidadeExemplo baseado no livro @james21:_introd_statis_learn, com dados obtidos de <https://www.kaggle.com/datasets/ashydv/advertising-dataset/data>.Este conjunto de dados contém $4$ colunas:* `tv`: verba (em milhares de dólares) gasta em publicidade na TV;* `radio`: verba (em milhares de dólares) gasta em publicidade no rádio;* `jornal`: verba (em milhares de dólares) gasta em publicidade em jornais;* `vendas`: receita das vendas (em milhares de dólares).Cada observação --- isto é, cada linha --- corresponde a um produto.### Leitura e limpeza```{r}publicidade <-read_csv('dados/advertising.csv',show_col_types =FALSE) %>% janitor::clean_names() %>%rename(jornal = newspaper,vendas = sales )publicidade %>%gt()```### Divisão em dados de treino e teste```{r}split <-initial_split(publicidade)treino <-training(split)teste <-testing(split)split```### Vendas por verba gasta em TV#### Análise exploratóriaComeçamos visualizando os dados:```{r}grafico <- treino %>%ggplot(aes(tv, vendas)) +geom_point()grafico```A correlação linear entre vendas e tv é```{r}cor(treino$vendas, treino$tv)```#### Modelo linear {#lm-vendas-tv}```{r}modelo <-lm(vendas ~ tv, data = treino)summary(modelo)``````{r}modelo_tidy <-tidy(modelo)modelo_tidy``````{r}b0 <- modelo_tidy$estimate[1]b1 <- modelo_tidy$estimate[2]``````{r}grafico +geom_abline(intercept = b0,slope = b1,color ='blue' )```A equação da reta é$$\begin{aligned} \widehat{\text{vendas}} &= \hat{\beta_0} + \hat{\beta_1} \cdot \text{tv} \\ &= `r b0` + `r b1` \cdot \text{tv}\end{aligned}$$## Teoria### Estimativas $\hat{\beta_0}$ e $\hat{\beta_1}$Os valores achados são estimativas para $\beta_0$ e $\beta_1$, baseadas nos dados do conjunto de treino.Por isso, os valores de `vendas` obtidos com esta equação também são estimativas.Vamos escrever estimativas com o acento circunflexo (chapéu) sobre os símbolos.De onde vêm os valores de $\hat{\beta_0}$ e $\hat{\beta_1}$?Resposta: são os valores que fazem com que a soma dos quadrados das distâncias verticais dos pontos à reta seja a menor possível. (Estas distâncias são chamadas de [resíduos]{.hl}.)[Consulte este material](https://fnaufel.github.io/probestr/regr.html#como-achar-a-equa%C3%A7%C3%A3o-da-melhor-reta-com-c%C3%A1lculo) para ver os detalhes sobre o cálculo de $\hat{\beta_0}$ e $\hat{\beta_1}$.### Erros-padrão das estimativasVamos pensar nas incertezas associadas aos valores de $\hat{\beta_0}$ e $\hat{\beta_1}$, com base na excelente discussão em [@de15:_stats, cap. 25].Quais são os fatores que afetam a nossa confiança na reta de regressão?Mais especificamente, [quais os fatores que afetam nossa confiança no valor estimado $\hat\beta_1$]{.hl} (a inclinação da reta)?#### Espalhamento dos pontos em volta da retaQuanto mais afastados da reta estiverem os dados, menor a nossa confiança de que a reta captura a variação de uma variável em função da outra.Observe a @fig-spread. O gráfico da esquerda nos dá mais certeza de que uma reta de regressão terá uma inclinação bem próxima da taxa de variação de $y$ em função de $x$ na população.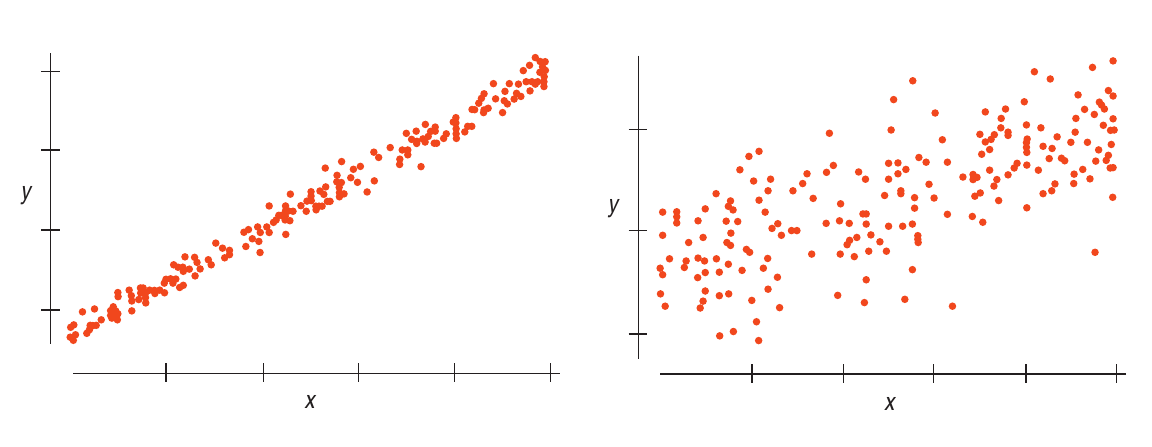{fig-alt="Dois gráficos de dispersão" #fig-spread width=100% fig-align="center"}Este espalhamento é medido pelo [desvio-padrão dos resíduos]{.hl}.[No exemplo das vendas](#lm-vendas-tv), este desvio-padrão dos resíduos é calculado como$$\displaystyle\sqrt{\frac{\sum_i (\text{vendas}_i - \widehat{\text{vendas}}_i)^2}{n-2}}$$No numerador, o valor $\text{vendas}_i - \widehat{\text{vendas}}_i$ é o resíduo da observação $i$.As `vendas` estimadas para cada valor de `tv` e os valores dos resíduos podem ser acessados assim:```{r}modelo_augment <-augment(modelo)modelo_augment %>%select(vendas, tv, .fitted, .resid)```Calculando o desvio-padrão dos resíduos:```{r}n <-nrow(modelo_augment)dp_residuos <-sqrt(sum(modelo_augment$.resid^2) / (n -2))dp_residuos```Este valor pode ser obtido na coluna `sigma` do *data frame* retornado pela função `glance`:```{r}modelo_glance <-glance(modelo)modelo_glance$sigma```::: {.callout-important}## Desvio-padrão dos resíduosNo geral, então, em uma regressão da variável $y$ sobre a variável $x$ com $n$ observações, o desvio-padrão dos resíduos é$$\displaystyles_{\text{residuos}} = \sqrt{\frac{\sum_i (y_i - \widehat{y}_i)^2}{n-2}}$$Pela @fig-spread e pelos comentários acima, quanto [maior]{.hl} o valor de $s_{\text{residuos}}$, [maior]{.hl} a nossa incerteza.:::#### Espalhamento de $x$Quanto maior o espalhamento dos valores de $x$, maior nossa confiança na reta de regressão, pois ela estará baseada em uma diversidade maior de valores.Observe a @fig-spread-x. O gráfico da direita tem um espalhamento maior dos valores de $x$. Uma reta de regressão, ali, parece estar mais bem "ancorada".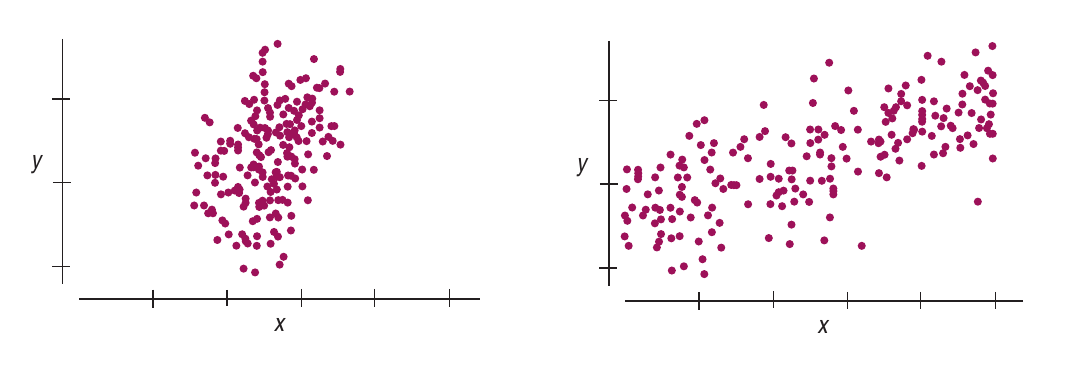{fig-alt="Dois gráficos de dispersão" #fig-spread-x width=100% fig-align="center"}O espalhamento de $x$ é medido pelo desvio-padrão, que é calculado da maneira usual. [No exemplo das vendas](#lm-vendas-tv), $s_x$, o desvio-padrão de `tv` é```{r}dp_x <- modelo_augment %>%pull(tv) %>%sd()dp_x```::: {.callout-important}## Desvio-padrão dos resíduosPela @fig-spread-x e pelos comentários acima, quanto [maior]{.hl} o valor de $s_x$, [menor]{.hl} a nossa incerteza.:::#### Quantidade de dadosUma reta baseada em mais pontos é mais confiável. Observe a @fig-n. {fig-alt="Dois gráficos de dispersão" #fig-n width=100% fig-align="center"}::: {.callout-important}## Quantidade de dadosPela @fig-n e pelos comentários acima, quanto [maior]{.hl} o valor de $n$, [menor]{.hl} a nossa incerteza.:::#### Juntando tudoVimos que* Quanto maior o desvio-padrão dos resíduos ($s_{\text{residuos}}$), [maior]{.hl} a incerteza.* Quanto maior o desvio-padrão da variável $x$ ($s_x$), [menor]{.hl} a incerteza.* Quanto maior a quantidade de dados ($n$), [menor]{.hl} a incerteza.Concluímos que a incerteza sobre nossa estimativa para $\beta_1$ (a inclinação da reta) é proporcional aos valores acima da seguinte maneira:$$EP(\beta_1) \propto \frac{s_{\text{residuos}}}{n \cdot s_x}$$onde estamos escrevendo a incerteza como [$EP(\beta_1)$]{.hl}, o [erro-padrão]{.hl} de $\beta_1$.::: {.callout-important}## Erro-padrão de $\beta_1$A fórmula exata para a incerteza sobre $\beta_1$ é$$EP(\beta_1) = \frac{s_{\text{residuos}}}{\sqrt{n - 1} \cdot s_x}$$:::[No exemplo das vendas](#lm-vendas-tv), usando as variáveis que já calculamos antes, este erro-padrão é```{r}dp_residuos / (sqrt(n -1) * dp_x)```Este valor aparece nos resultados de `lm` como `std.error`:```{r}modelo_tidy```#### Erro-padrão do intercepto::: {.callout-important}## Erro-padrão de $\beta_0$Para o intercepto $\beta_0$, o raciocínio é análogo.A fórmula exata para a incerteza sobre $\beta_0$ é$$EP(\beta_0) = $$:::??? ISLR p. 76## Visão geométrica@faraway16:_linear_model_r### Um pequeno exemploPara podermos visualizar a geometria, vamos considerar um conjunto de dados com apenas $3$ observações.A variável `x` é o único preditor, e a variável `y` é a resposta.```{r}df <-tibble(x =1:3,y =c(4, 3, 8))``````{r}#| echo: falsedf %>%gt()```Graficamente:```{r}#| echo: falsep <- df %>%ggplot(aes(x, y)) +geom_point() +scale_x_continuous(breaks =0:4, limits =c(0, 4)) +scale_y_continuous(breaks =0:9, limits =c(0, 9)) +coord_equal()p```Com um único preditor, este é um exemplo de regressão simples. Queremos achar uma equação da forma$$\hat y = \beta_0 + \beta_1x$$com valores de $\beta_0$ e $\beta_1$ que garantam a menor soma dos quadrados dos resíduos.Usamos o R para achar os coeficientes e outras informações sobre este modelo:```{r}modelo <-lm(y ~ x, df)summary(modelo)``````{r}#| echo: falseb0 <-coef(modelo)[1]b1 <-coef(modelo)[2]```A equação da reta que procuramos é$$\hat y = `r b0` + `r b1` x$$No gráfico, os valores de $\hat y$, para cada valor de $x$, são mostrados em vermelho. A reta de regressão é mostrada em azul:```{r}#| echo: falsep +geom_abline(intercept = b0, slope = b1, color ='blue') +geom_point(aes(y =fitted.values(modelo)), color ='red')```Os valores de $y$, os valores previstos e os resíduos são```{r}#| echo: falsemodelo_aumentado <- modelo %>%augment()modelo_aumentado %>%select(x, y, previsto = .fitted, resíduo = .resid) %>%gt()```Usando Álgebra Linear, vamos encarar este modelo de outra forma.A coluna `y` dos dados é representada pelo vetor$$\vec{Y} = \begin{bmatrix} 4 \\ 3 \\ 8\end{bmatrix}$$Vamos definir a seguinte matriz:$$\vec{X} = \begin{bmatrix} 1 & 1 \\ 1 & 2 \\ 1 & 3\end{bmatrix}$$Nesta matriz, a segunda coluna corresponde à coluna `x` dos dados. A primeira coluna, com valores $1$, está ali para podermos escrever o modelo como a equação matricial$$\vec{\widehat{Y}} = \vec{X} \cdot \begin{bmatrix} \beta_0 \\ \beta_1\end{bmatrix}$$que, de forma mais detalhada, é$$\begin{bmatrix} \widehat{y_1} \\ \widehat{y_2} \\ \widehat{y_3}\end{bmatrix}=\begin{bmatrix} 1 & 1 \\ 1 & 2 \\ 1 & 3\end{bmatrix}\cdot \begin{bmatrix} \beta_0 \\ \beta_1\end{bmatrix}$$ou, ainda,$$\begin{bmatrix} \widehat{y_1} \\ \widehat{y_2} \\ \widehat{y_3}\end{bmatrix}=\begin{bmatrix} \beta_0 + \phantom{1\cdot{}}\beta_1 \\ \beta_0 + 2\cdot \beta_1 \\ \beta_0 + 3\cdot \beta_1\end{bmatrix}$$ou, explicitando os vetores que correspondem às colunas da matriz $\vec{X}$:$$\begin{bmatrix} \widehat{y_1} \\ \widehat{y_2} \\ \widehat{y_3}\end{bmatrix}=\beta_0 \cdot \begin{bmatrix} 1 \\ 1 \\ 1\end{bmatrix}+ \beta_1 \cdot\begin{bmatrix} 1 \\ 2 \\ 3\end{bmatrix}$$ {#eq-modelo}Agora, as considerações geométricas:1. As colunas `x` e `y` do conjunto de dados são vetores com $3$ componentes, que vivem em $\reais^3$.1. O vetor $\vec{\widehat Y}$ também tem $3$ componentes, mas a @eq-modelo está dizendo que $\vec{\widehat Y}$ é uma combinação linear dos dois vetores (linearmente independentes) $[1\ 1\ 1]^T$ e $[1\ 2\ 3]^T$.1. Os dois vetores $[1\ 1\ 1]^T$ e $[1\ 2\ 3]^T$ não são capazes de gerar todo o espaço $\reais^3$; o espaço gerado por eles é um plano.1. O vetor $\vec Y$ (com os valores verdadeiros da variável de resposta $y$) não está no plano gerado pelos vetores $[1\ 1\ 1]^T$ e $[1\ 2\ 3]^T$ (verifique).1. A relação verdadeira entre $\vec Y$ e $\vec X$ é $$ \begin{bmatrix} y_1 \\ {y_2} \\ {y_3} \end{bmatrix} = \beta_0 \cdot \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} + \beta_1 \cdot \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} + \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \end{bmatrix} $$ onde os valores $\varepsilon_i$ são os erros que o modelo não consegue capturar.1. Estes erros $\varepsilon_i$ são estimados pelos resíduos $\widehat{\varepsilon_i}$, de maneira que podemos escrever $$ \begin{bmatrix} \widehat{y_1} \\ \widehat{y_2} \\ \widehat{y_3} \end{bmatrix} = \beta_0 \cdot \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} + \beta_1 \cdot \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} + \begin{bmatrix} \widehat{\varepsilon_1} \\ \widehat{\varepsilon_2} \\ \widehat{\varepsilon_3} \end{bmatrix} $$ O vetor de resíduos é $$ \vec{\widehat{\varepsilon}} = \begin{bmatrix} \widehat{\varepsilon_1} \\ \widehat{\varepsilon_2} \\ \widehat{\varepsilon_3} \end{bmatrix} = \begin{bmatrix} \phantom{-}1 \\ -2 \\ \phantom{-}1 \end{bmatrix} $$A situação é mostrada na figura: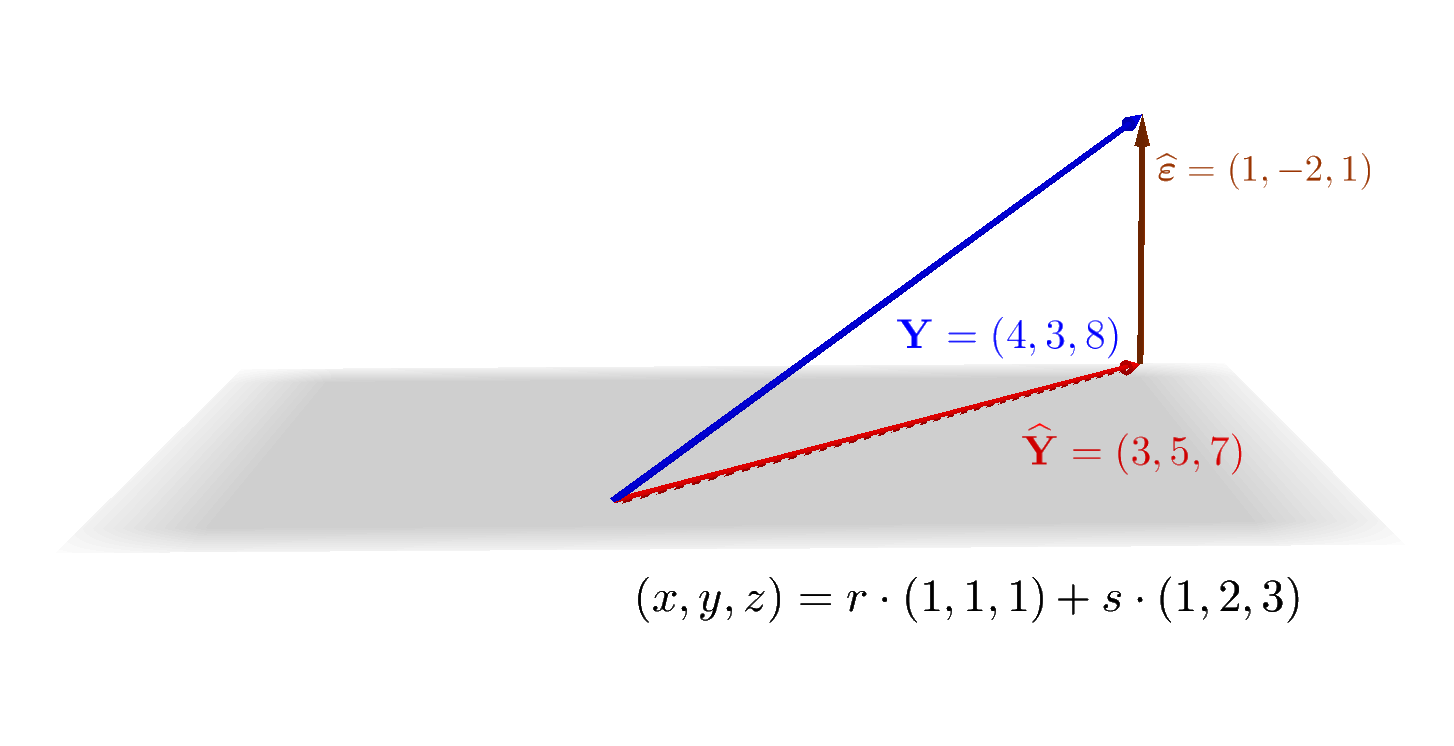O plano cinza é o espaço gerado pelos vetores $[1\ 1\ 1]^T$ e $[1\ 2\ 3]^T$. Na equação paramétrica deste plano, $r$ e $s$ correspondem aos valores possíveis de $\beta_0$ e $\beta_1$, respectivamente.O vetor $\vec{\widehat{Y}}$ (dos valores previstos pelo modelo) é a projeção ortogonal do vetor $\vec{Y}$ (dos valores verdadeiros da variável de resposta) sobre o plano gerado pelas colunas da matriz $\vec X$. Mais abaixo, vamos ver os detalhes desta projeção. O importante é entender que, quaisquer que sejam os valores de $\beta_0$ e $\beta_1$, o vetor $\vec{\widehat{Y}}$ de valores previstos vai estar sempre limitado ao plano gerado pelas colunas da matriz $\vec{X}$. Isto corresponde à intuição de que estamos perdendo informação ao tentar representar objetos de dimensão $3$ (o número de observações do conjunto de dados) em um espaço de dimensão $2$ (o número de parâmetros do modelo: $\beta_0$ e $\beta_1$). ???