Capítulo 14 Covariância e correlação

14.1 Vídeo

14.2 Exemplo: altura e peso

Pessoas mais altas tendem a ser mais pesadas?

Temos dados de \(80\) alunos e alunas, com alturas em cm e pesos em kg:

• O gráfico de dispersão (scatter plot) é o ideal para visualizar a correlação entre duas variáveis numéricas:

  peso_altura %>% 
    ggplot(aes(altura, peso)) +
      geom_point() +
      labs(
        x = 'altura (cm)',
        y = 'peso\n(kg)'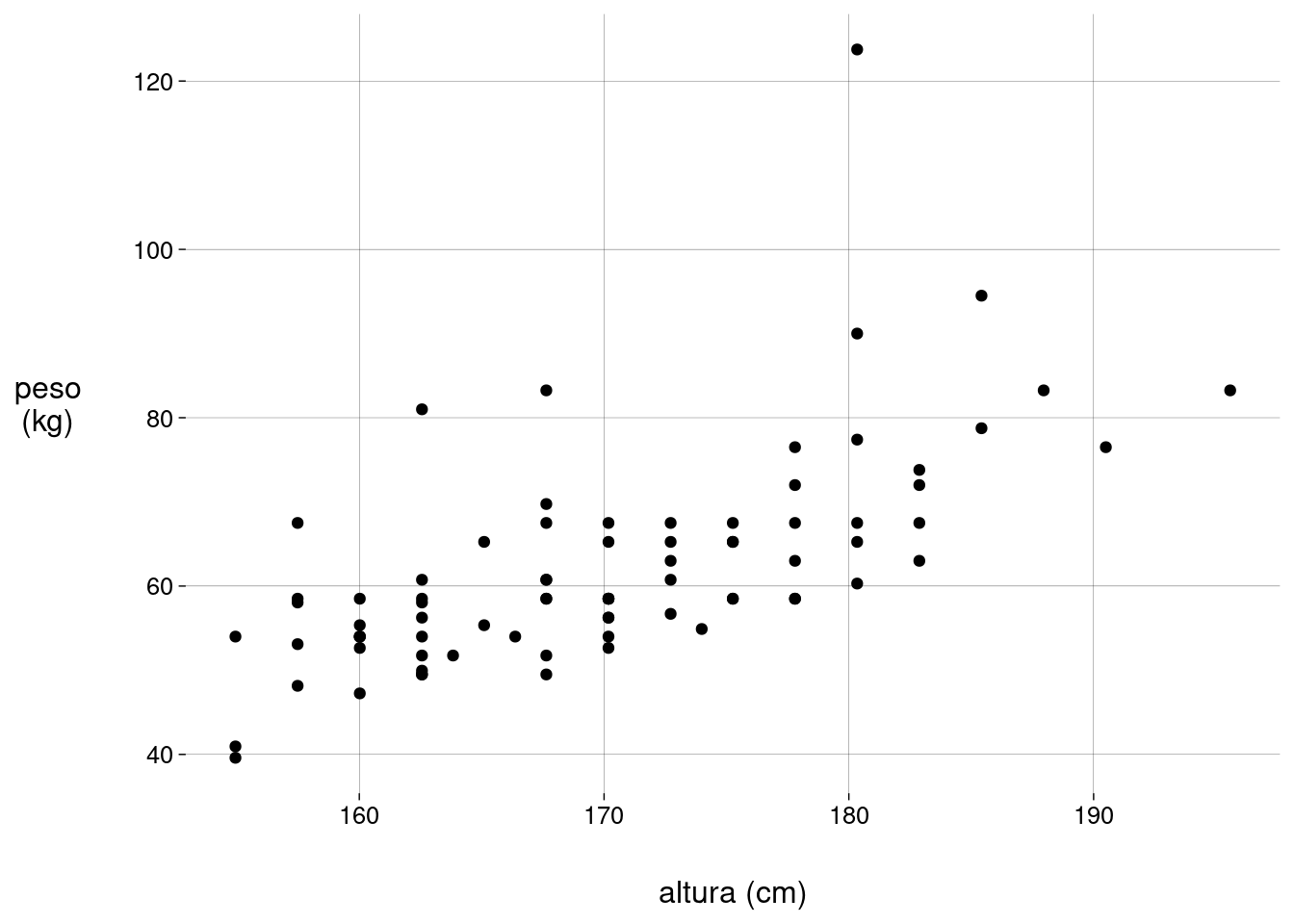
      )

  

14.3 Correlação linear

• Vamos subtrair, de cada peso, a média dos pesos; vamos subtrair, de cada altura, a média das alturas.

  peso_altura <- peso_altura %>% 
    mutate(
      altura_desvio = altura - mean(altura),
      peso_desvio = peso - mean(peso)
    )

• O novo scatter plot tem a mesma forma. Só mudam as escalas: a altura média e o peso médio agora são iguais a zero.

  peso_altura %>% 
    ggplot(aes(altura_desvio, peso_desvio)) +
      geom_point() +
      labs(
        x = 'desvios altura (cm)',
        y = 'desvios peso\n(kg)'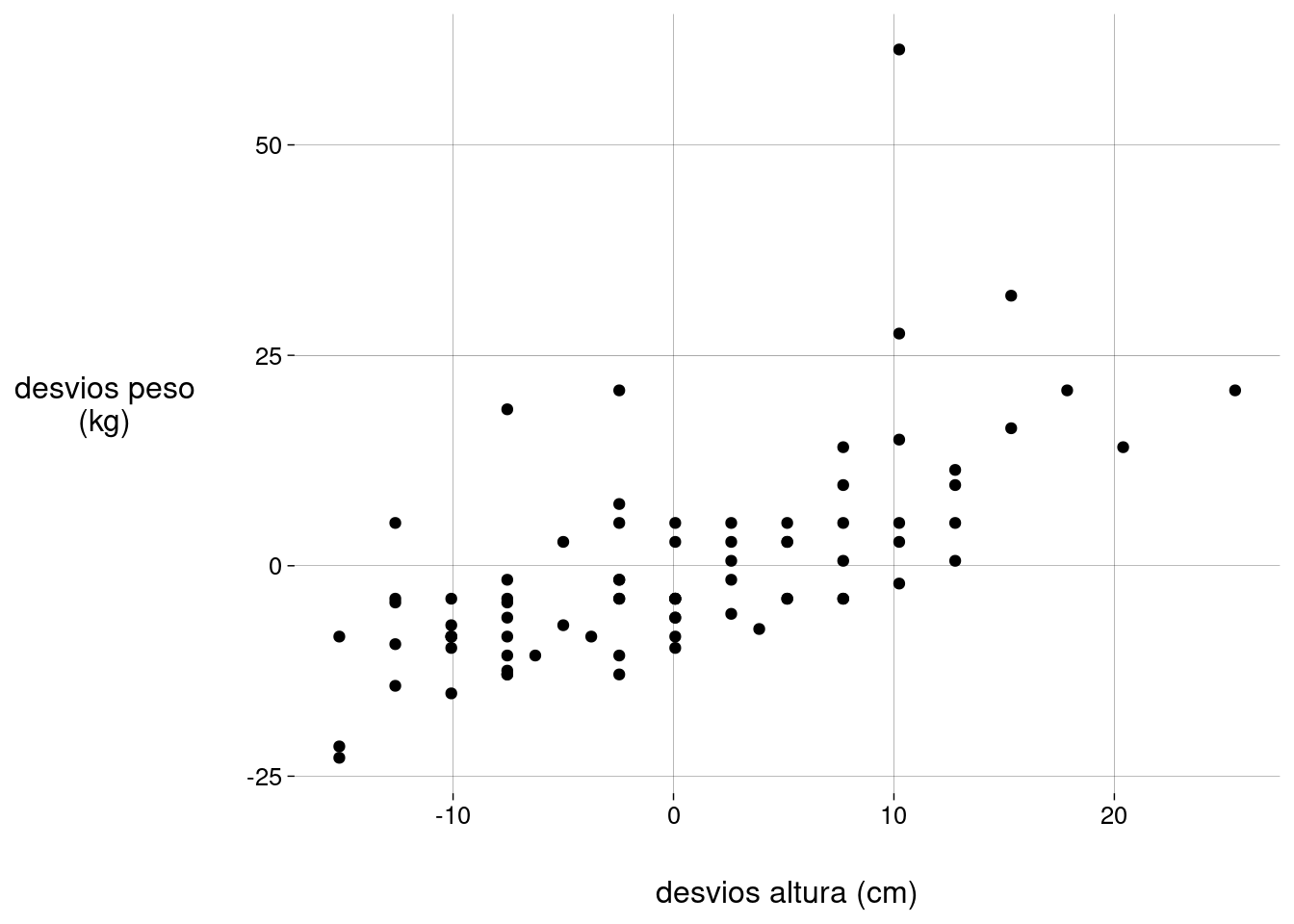
      )

  

• Quando o desvio da altura e o desvio do peso têm o mesmo sinal, os valores têm uma associação positiva: ou altura e peso estão ambos acima da média, ou ambos abaixo da média.

• Colorindo os pontos de acordo com a associação:

  peso_altura %>% 
    ggplot(aes(altura_desvio, peso_desvio)) +
      geom_point(
        data = . %>% filter(altura_desvio * peso_desvio >= 0),
        color = 'blue'
      ) +
      geom_point(
        data = . %>% filter(altura_desvio * peso_desvio < 0),
        color = 'red'
      ) +
      geom_hline(aes(yintercept = 0), linetype = 'dashed') +
      geom_vline(aes(xintercept = 0), linetype = 'dashed') +
      labs(
        x = 'desvios altura (cm)',
        y = 'desvios peso\n(kg)'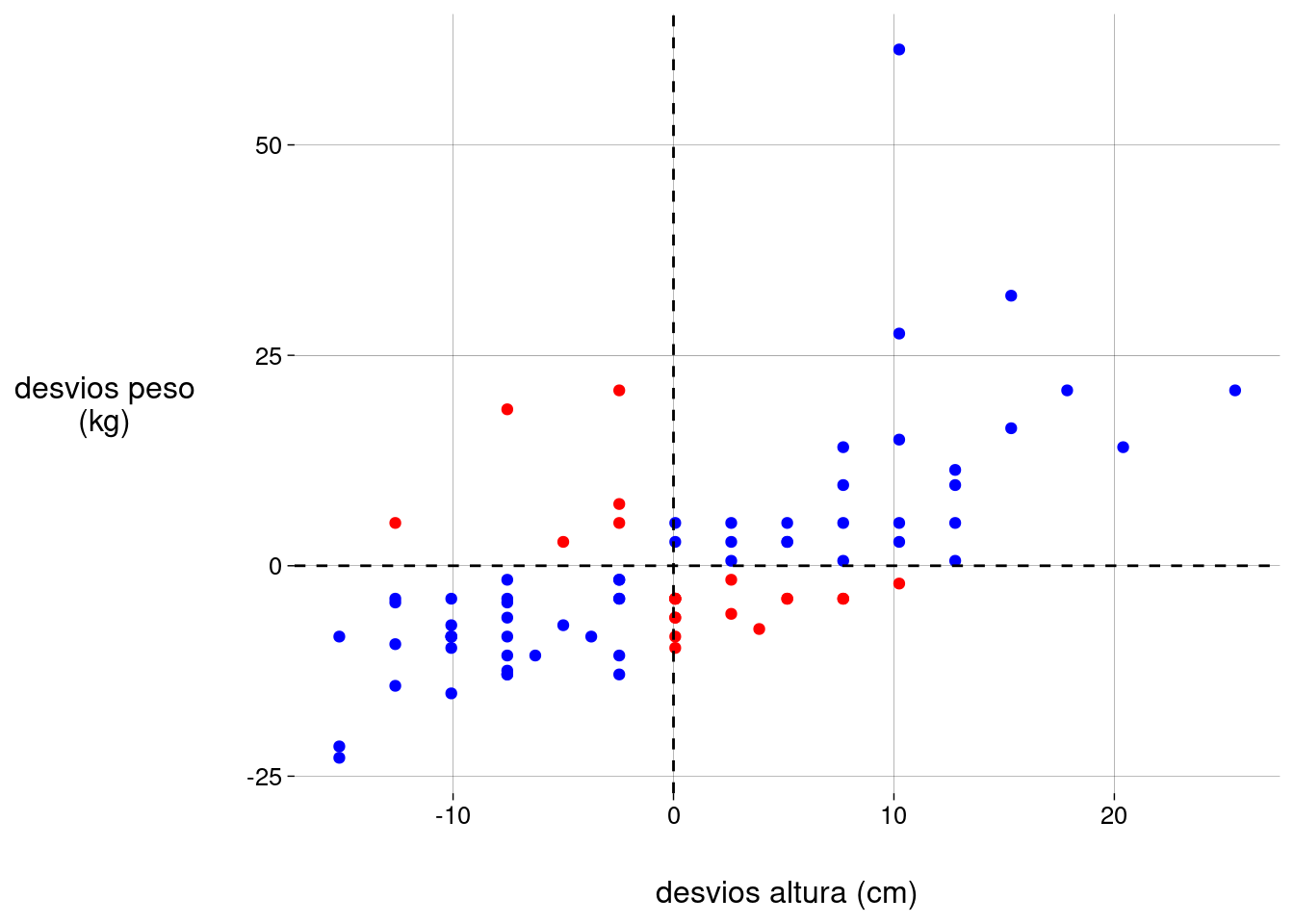
      )

  

14.4 Covariância

• Examine o código acima: para verificar se os desvios têm o mesmo sinal, basta verificar se o produto dos desvios é positivo.

• E mais: quanto maior o produto dos desvios, mais acima (ou mais abaixo) das respectivas médias os desvios estão, ao mesmo tempo. Ou seja, maior a associação entre as duas variáveis.

• Estamos falando de

  \[ \text{produto dos desvios}_i = (\text{altura}_i - E(\text{altura})) \cdot (\text{peso}_i - E(\text{peso})) \]

• Podemos calcular os produtos dos desvios e achar a média destes produtos. O resultado vai ser a covariância:

  \[ \text{Cov}(\text{altura}, \text{peso}) = \frac{ \sum_i\; [(\text{altura}_i - E(\text{altura})) \cdot (\text{peso}_i - E(\text{peso}))] }{n} \]

• Ou, de forma mais compacta,

  \[ \text{Cov}(\text{altura}, \text{peso}) = E[(\text{altura} - E(\text{altura})) \cdot (\text{peso} - E(\text{peso}))] \]

• O R usa \(n - 1\) no denominador, em vez de \(n\). Isto significa que o R calcula a covariância amostral, que serve como um estimador da covariância populacional.

• Calculando:

  peso_altura %>% 
    mutate(produto = altura_desvio * peso_desvio) %>% 
    summarize(cov = sum(produto)/(nrow(.) - 1)) %>% 
    pull(cov)

  ## [1] 73,8935

14.4.1 Em R

cov(peso_altura$altura, peso_altura$peso)

## [1] 73,8935

14.4.2 Exercícios

• Qual é a unidade da covariância? Examine as fórmulas acima para responder.

• Execute o bloco abaixo com diversos valores de k, inclusive valores negativos.

  k <- 10
  
  X <- 1:5
  Y <- k * X
  
  tibble(X, Y) %>% 
    ggplot(aes(X, Y)) +
      geom_point(size = 2) +
      labs(
        title = paste('cov(X, Y) =', cov(X, Y))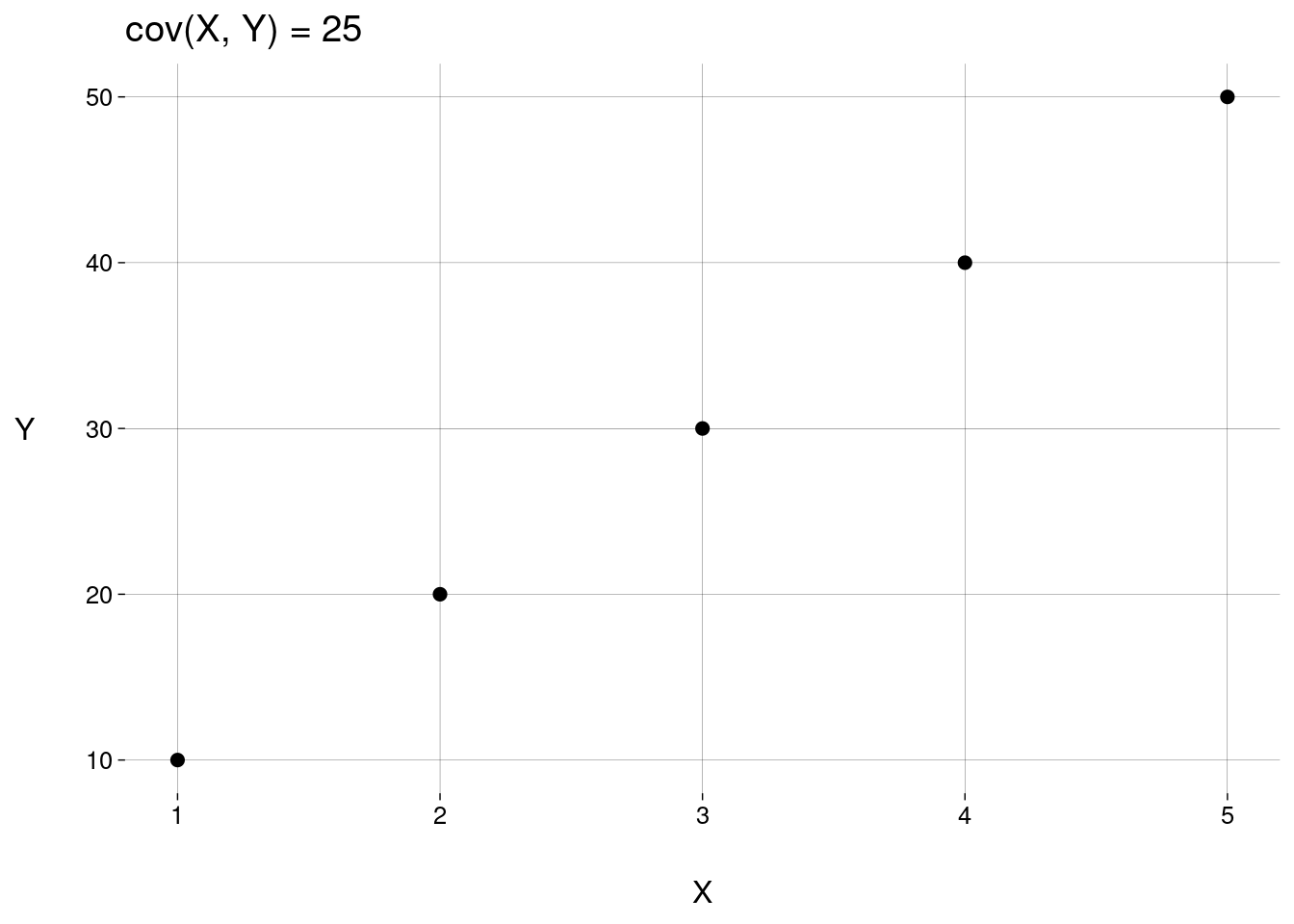
      )

  

• Qual a covariância máxima entre duas variáveis? E a mínima?

• Usando as propriedades do valor esperado, mostre que, para quaisquer variáveis aleatórias \(X\) e \(Y\)

  \[ \text{Cov}(X,Y) \quad=\quad E\big[(X - E(X)) \cdot (Y - E(Y))\big] \quad=\quad E(XY) - E(X)E(Y) \]

• Lembre-se de que a variância de uma variável aleatória \(X\) pode ser escrita como

  \[ \text{Var}(X) = E(X^2) - [E(X)]^2 \]

  Alguma semelhança entre esta expressão e a expressão do item anterior?

• Qual a covariância de uma variável aleatória \(X\) com ela mesma?

• O R usa \(n - 1\) no denominador da covariância. Mostre que definir a covariância como \[ \text{Cov}(X, Y) = \frac{1}{n - 1} \cdot \sum_{i = 1}^n \big[(x_i - E(X)) \cdot (y_i - E(Y)) \big] \]

  é equivalente a

  \[ \text{Cov}(X, Y) = \frac{n}{n-1} \cdot \big[ E(XY) - E(X)E(Y) \big] \]

• Usando o data frame peso_altura, compute o valor da expressão acima e compare com o resultado de cov(peso_altura$altura, peso_altura$peso).

14.5 Coeficiente de correlação linear

• Vamos padronizar as alturas e pesos (i.e., subtrair a média e dividir pelo desvio-padrão):

  peso_altura <- peso_altura %>% 
    mutate(
      altura_padronizada = scale(altura),
      peso_padronizado = scale(peso)
    )

• E construir o scatter plot:

  peso_altura %>% 
    ggplot(aes(altura_padronizada, peso_padronizado)) +
      geom_point(
        data = . %>% filter(altura_padronizada * peso_padronizado >= 0),
        color = 'blue'
      ) +
      geom_point(
        data = . %>% filter(altura_padronizada * peso_padronizado < 0),
        color = 'red'
      ) +
      geom_hline(aes(yintercept = 0), linetype = 'dashed') +
      geom_vline(aes(xintercept = 0), linetype = 'dashed') +
      labs(
        x = 'altura padronizada',
        y = 'peso\npadronizado'
      )

  ## Warning: Using one column matrices in `filter()` was deprecated in dplyr 1.1.0.
  ## ℹ Please use one dimensional logical vectors instead.
  ## This warning is displayed once every 8 hours.
  ## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
  ## generated.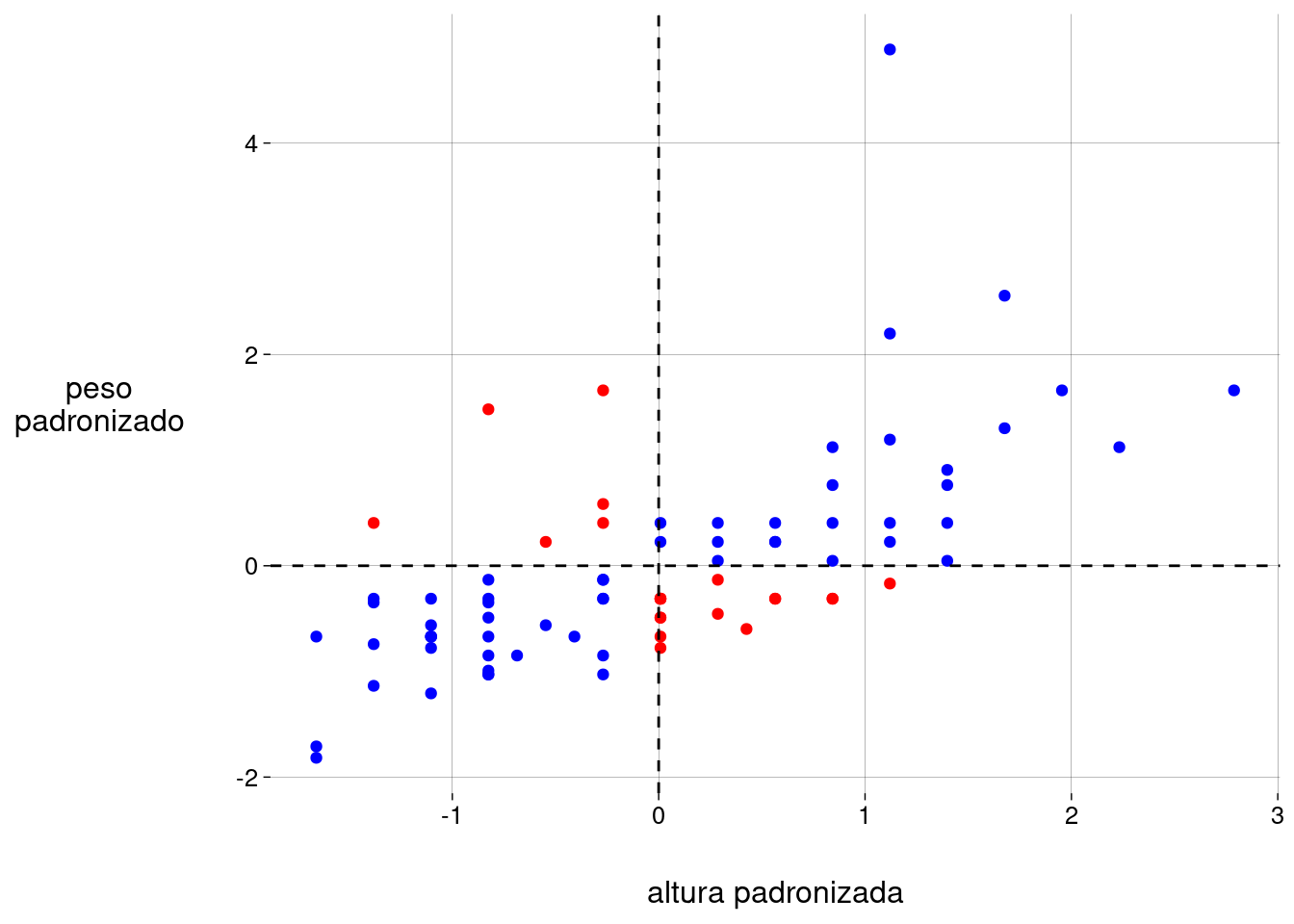

  

• Ou seja, agora as variáveis são

  \[ Z_A = \frac{\text{altura} - E(\text{altura})}{DP(\text{altura})} \]

  e

  \[ Z_P = \frac{\text{peso} - E(\text{peso})}{DP(\text{peso})} \]

• A covariância entre elas é

  cov(peso_altura$peso_padronizado, peso_altura$altura_padronizada)

  ##           [,1]
  ## [1,] 0,6440311

• Quando padronizamos as duas variáveis, a covariância entre elas se chama correlação.

• O coeficiente de correlação amostral é este valor.

  \[ r = \frac{\sum x_i y_i}{n - 1} \]

  onde \(X\) e \(Y\) são variáveis padronizadas.

• Alguns livros chamam o coeficiente de correlação de \(\rho\) em vez de \(r\).

• O coeficiente de correlação sempre está entre \(-1\) e \(1\), inclusive.

• Fórmulas alternativas para o coeficiente de correlação entre \(X\) e \(Y\) (não necessariamente padronizadas):

  \[ r = \frac{\text{Cov}(X, Y)}{DP_X \cdot DP_Y} \]

  e

  \[ r = \frac{ \sum(x_i - E(X))\cdot(y_i - E(Y)) }{ \sqrt{\sum(x_i - E(X))^2\cdot(y_i - E(Y))^2} } \]

14.5.1 Em R

cor(peso_altura$peso, peso_altura$altura)

## [1] 0,6440311

14.5.2 Exercícios

• Qual a unidade do coeficiente de correlação?

• Execute o bloco abaixo com diversos valores de k, inclusive valores negativos.

  k <- 10
  
  X <- 1:5
  Y <- k * X
  
  tibble(X, Y) %>% 
    ggplot(aes(X, Y)) +
      geom_point(size = 2) +
      labs(
        title = paste('cor(X, Y) =', cor(X, Y))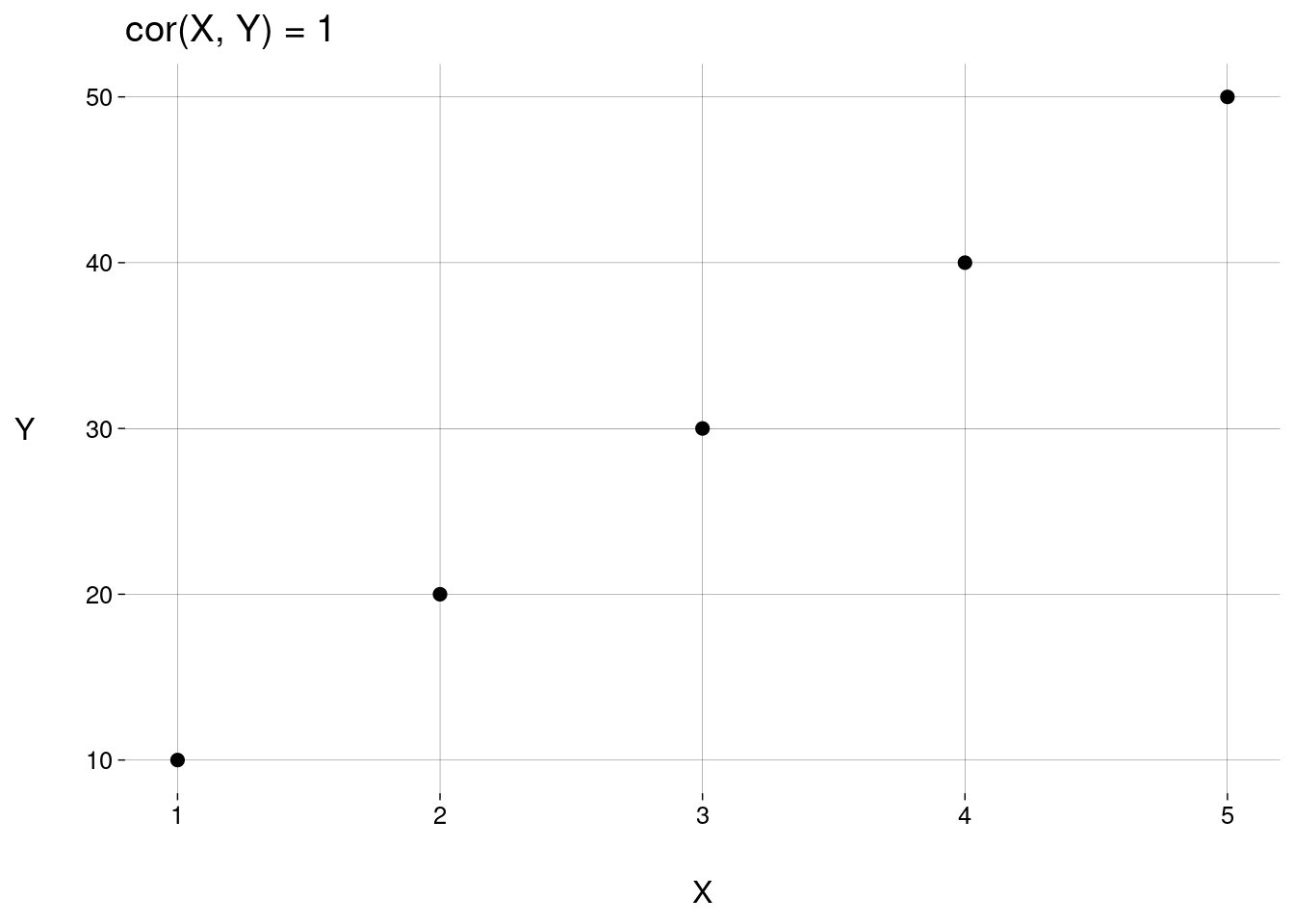
      )

  

• Como você explica os valores de \(\text{cor}(X,Y)\) no item anterior, em comparação com os valores de \(\text{cov}(X,Y)\) nesse outro exercício?

• Qual a correlação de uma variável aleatória \(X\) com ela mesma?

• Usando o data frame peso_altura, compute o valor do coeficiente de correlação entre peso e altura usando as fórmulas alternativas.

14.5.3 Observações importantes

A correlação é linear

(https://commons.wikimedia.org/wiki/File:Pearson_Correlation_Coefficient_and_associated_scatterplots.png)

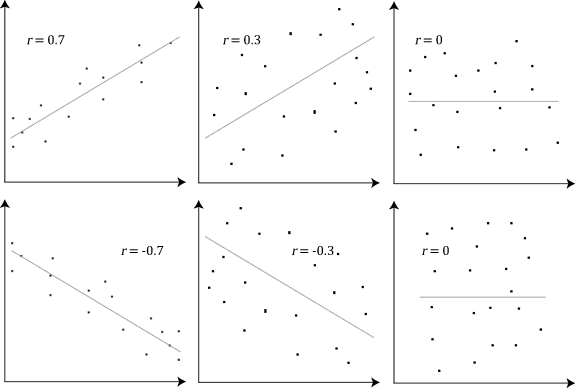
• Se \(r > 0\), valores altos de uma variável tendem a corresponder a valores altos da outra variável.

• Se \(r < 0\), valores altos de uma variável tendem a corresponder a valores baixos da outra variável.

• Se \(r = 0\), não há correlação linear entre as variáveis.

• O coeficiente de correlação \(r\) só mede a correlação linear entre duas variáveis.

  

(https://commons.wikimedia.org/wiki/File:Correlation_examples2.svg)

• Exemplos de Anscombe, com \(4\) conjuntos de dados com o mesmo valor de \(r\) mas com associações muito diferentes entre as variáveis:

  anscombe

  desenhar <- function(n) {
  
    nomex <- paste0('x', n)
    nomey <- paste0('y', n)
    r <- cor(anscombe[[nomex]], anscombe[[nomey]]) %>% round(2)
  
    anscombe %>% 
      ggplot(aes(.data[[nomex]], .data[[nomey]])) +
        geom_point() +
        geom_smooth(method = 'lm', se = FALSE) +
        labs(
          title = paste('r =', r)
        )
  
  }
  
  
  plots <- map(1:4, desenhar)
  plots[[1]] + plots[[2]] + plots[[3]] + plots[[4]]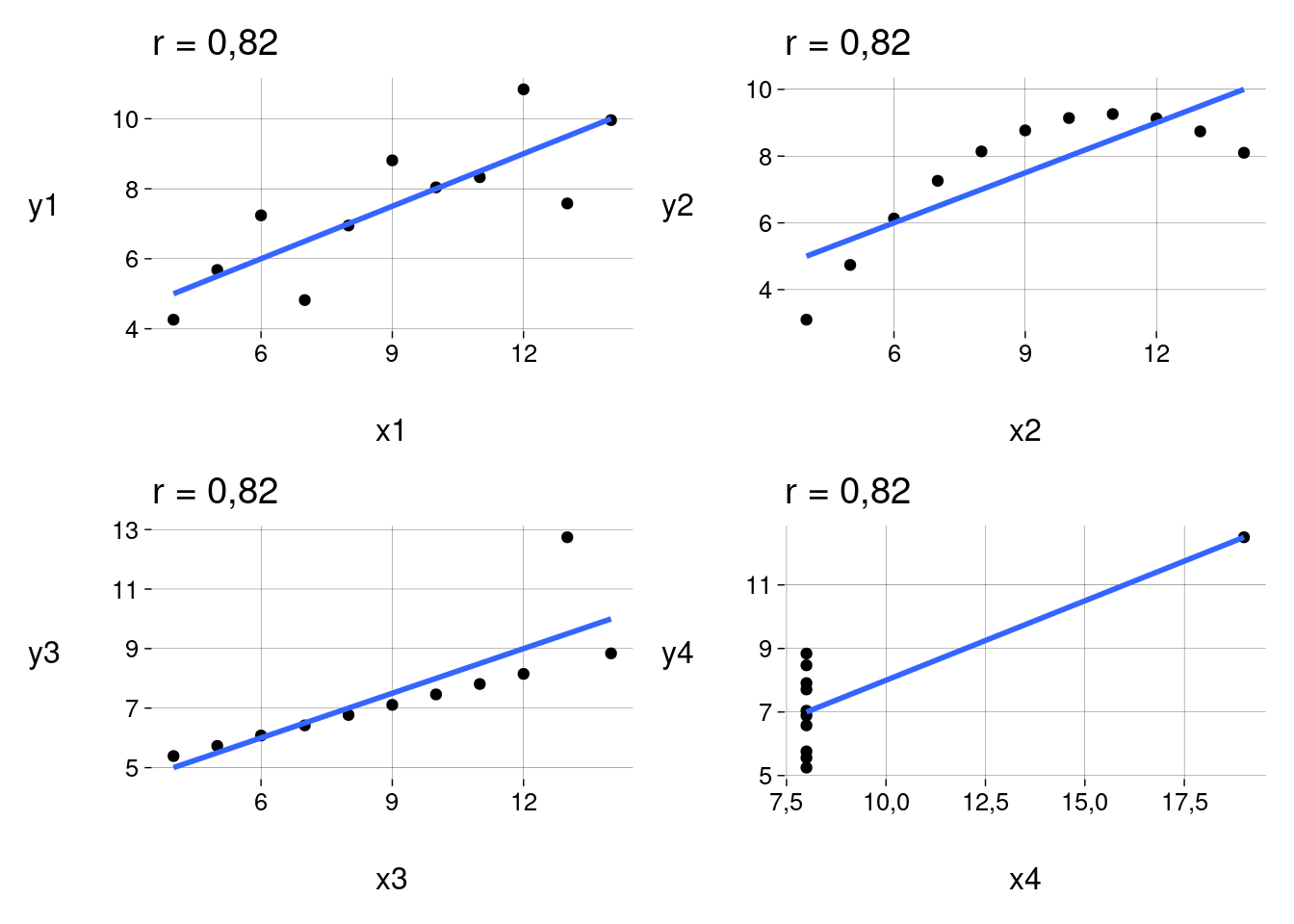 

  

• Conclusões:

  • O valor de \(r\) só reflete correlação linear.

  • A presença de outliers produz valores não-confiáveis de \(r\).

Correlação \(\neq\) causação

• Dados coletados em Oldenburg, na Alemanha, nos anos \(1930\), mostrando a correlação entre a quantidade de cegonhas e a população (de pessoas) na cidade:

  df <- read_csv('data/Storks.csv') %>% 
    transmute(
      cegonhas = Storks,
      pessoas = Population
    ) 
  
  r <- cor(df$cegonhas, df$pessoas) %>% round(2)
  
  df %>% 
    ggplot(aes(cegonhas, pessoas)) +
      geom_point() +
      labs(
        title = paste('r =', r)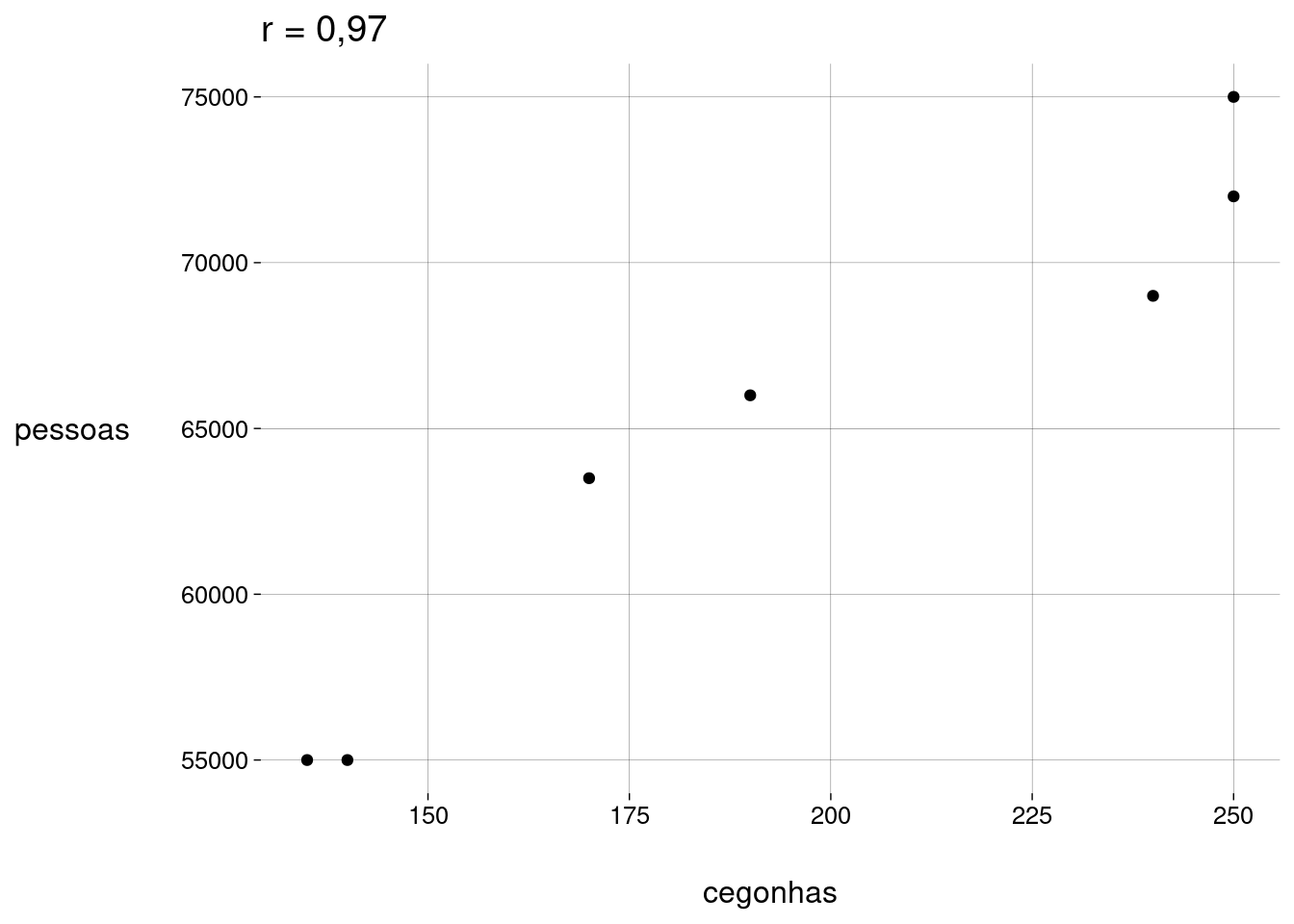
      )

  

• Variável oculta: quantidade de casas com chaminé.

• Ou coincidência: http://tylervigen.com/spurious-correlations

14.6 Teste e intervalo de confiança para a correlação

14.6.1 Exemplo: PIB e CO\(_2\)

• Em uma amostra de \(10\) países, examinamos o PIB (em trilhões de dólares) e a quantidade de emissões de CO\(_2\) (em milhões de toneladas):

• Gráfico:

  df %>% 
    ggplot(aes(PIB, emissões)) +
      geom_point() +
      scale_y_continuous(
        'emissões\n(milhões de\ntoneladas)',
        breaks = seq(0, 1200, 200),
        limits = c(0, 1200)
      ) +
      scale_x_continuous(
        'PIB (trilhões US$)',
        breaks = 0:6,
        limits = c(0, 6)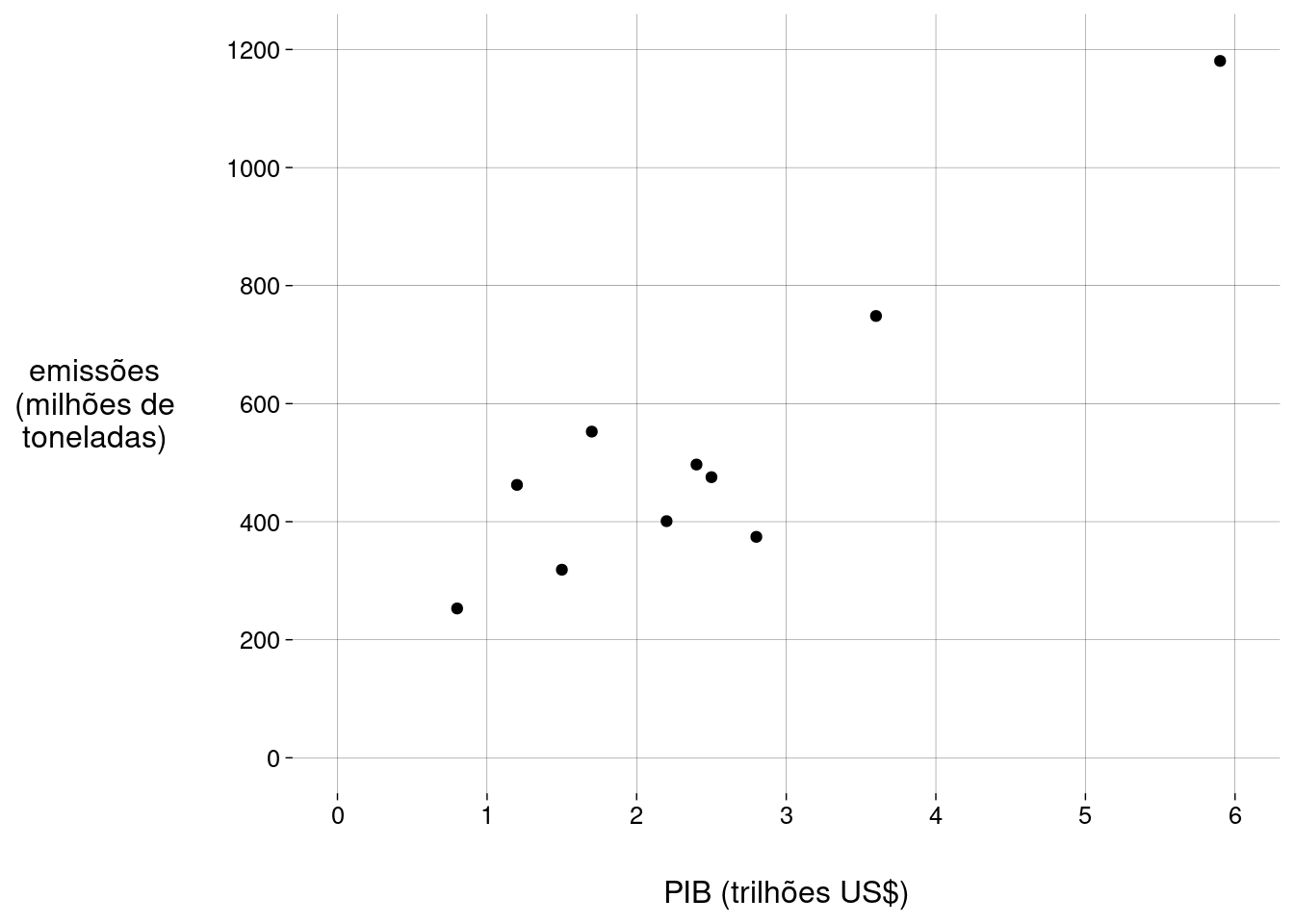
      )

  

• O coeficiente de correlação amostral é

  cor(df$PIB, df$emissões)

  ## [1] 0,9115924

• Como esta é uma amostra, devemos calcular um intervalo de confiança para o coeficiente de correlação populacional.

• O R faz isto com a função cor.test:

  ct <- cor.test(df$PIB, df$emissões)
  ct

  ## 
  ##  Pearson's product-moment correlation
  ## 
  ## data:  df$PIB and df$emissões
  ## t = 6,272, df = 8, p-value = 0,0002399
  ## alternative hypothesis: true correlation is not equal to 0
  ## 95 percent confidence interval:
  ##  0,6618340 0,9791965
  ## sample estimates:
  ##       cor 
  ## 0,9115924

• Conclusão: com \(95\%\) de confiança, estimamos que o coeficiente de correlação populacional é capturado pelo intervalo

  \[ [\quad 0{,}66 \quad ;\quad 0{,}98 \quad] \]

14.6.2 Exercícios

• Qual é o tipo de teste usado por cor.test?

• Quais são as hipóteses do teste?

• Como é calculado o valor da estatística do teste (\(6{,}272\) no exemplo acima)?

• Como é calculado o valor \(p\) (\(0{,}0002399\) no exemplo acima)?

• Implemente uma função em R para fazer o mesmo que cor.test.

14.7 Transformações

14.7.1 Exemplo: fotografia

• Ao configurar uma câmera para tirar uma foto, você deve ajustar a velocidade do obturador e a abertura do diafragma.

• O fabricante de uma câmera recomenda os seguintes valores:

• Gráfico:

  df %>% 
    ggplot(aes(velocidade, abertura)) +
      geom_point()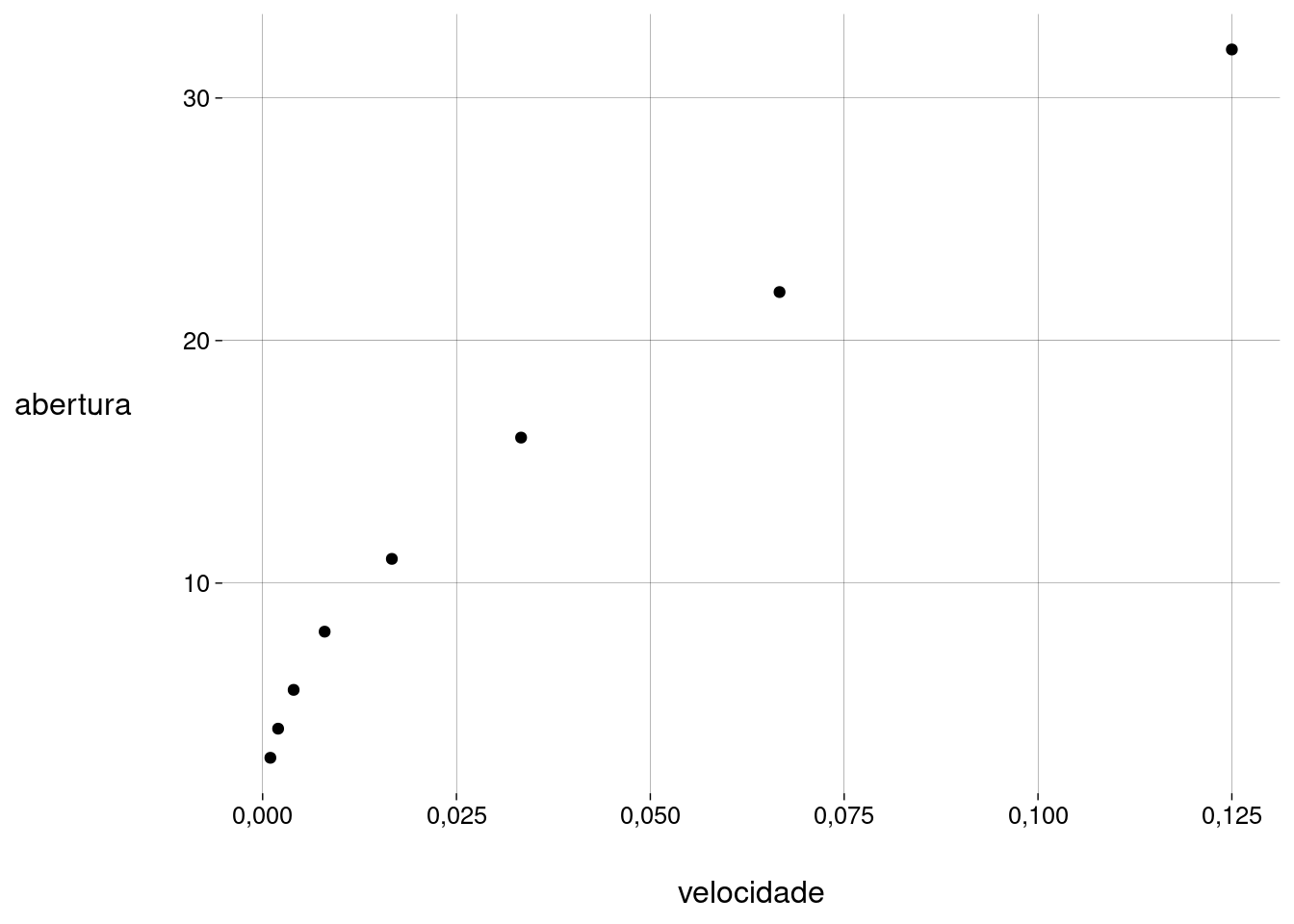

  

• Coeficiente de correlação:

  cor(df$velocidade, df$abertura)

  ## [1] 0,978669

• Este já é um coeficiente de correlação alto, mas o gráfico mostra que também existe uma associação não-linear entre as variáveis.

• Vamos transformar os valores de uma das variáveis para tornar a correlação mais linear (menos curva):

  df <- df %>% 
    mutate(quad_abertura = abertura^2)

  df %>% 
    ggplot(aes(velocidade, quad_abertura)) +
      geom_point() +
      labs(y = 'abertura²')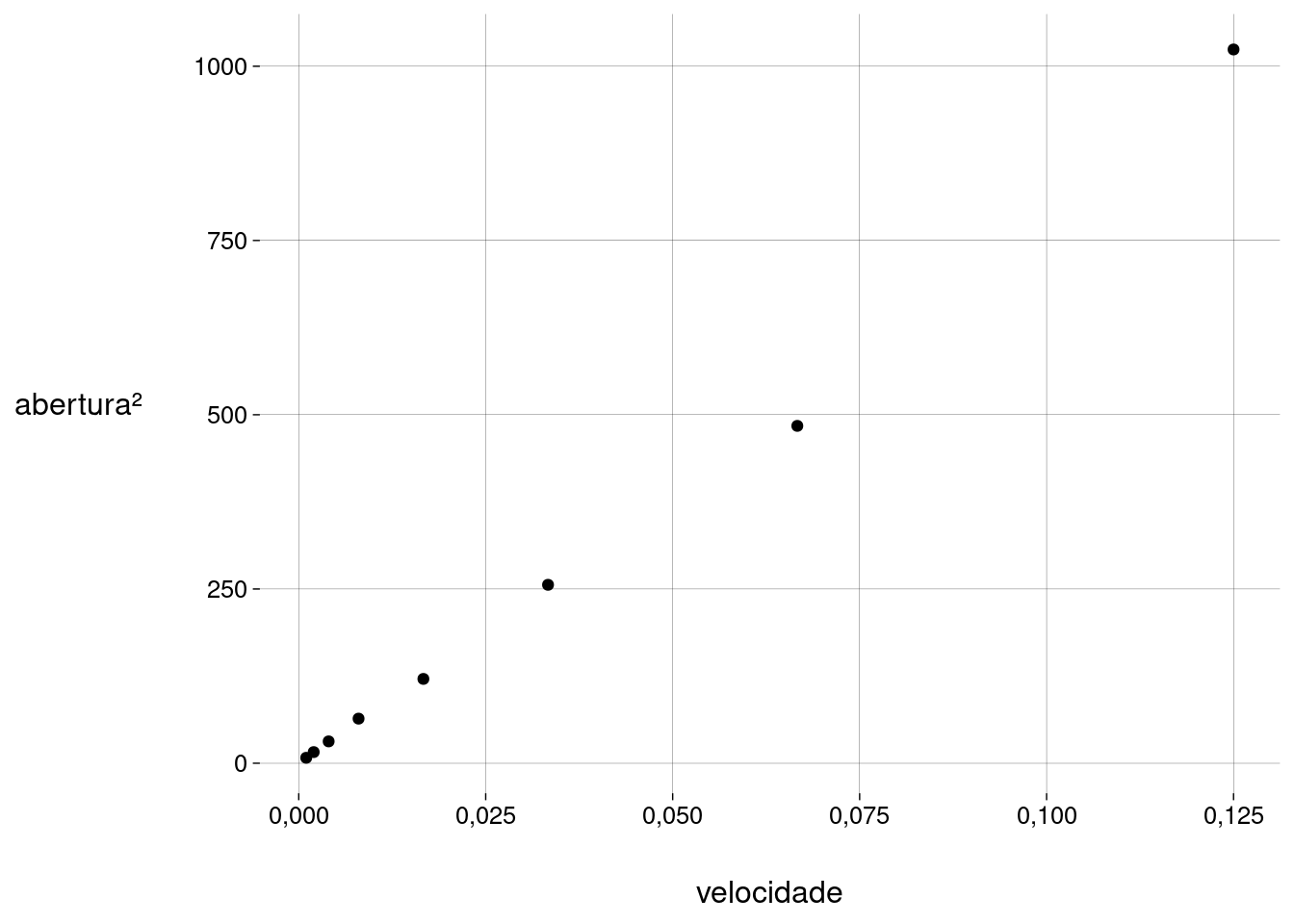

  

• A correlação linear agora é

  cor(df$velocidade, df$quad_abertura)

  ## [1] 0,9983046

14.7.2 Funções usadas em transformações

• \(f(x) = x^2\): útil quando os valores originais têm cauda longa à esquerda, ou quando os valores originais têm concavidade para baixo.

• \(f(x) = \sqrt{x}\): útil para valores que representam contagens.

• \(f(x) = \log x\): útil para valores positivos, que crescem de acordo com percentagens, como salários, populações etc. Como \(\log 0\) não é definido, você pode precisar acrescentar uma constante \(\varepsilon\) aos valores antes da transformação.

• \(f(x) = -\frac1{\sqrt{x}}\): o sinal negativo mantém a ordenação dos valores.

• \(f(x) = -\frac1x\): útil para razões, como km/h. O sinal negativo mantém a ordenação dos valores. Como \(y/0\) não é definido, você pode precisar acrescentar uma constante \(\varepsilon\) aos valores antes da transformação.

14.7.3 Exercício

• Aplique as outras transformações da lista acima aos valores da variável abertura. Desenhe gráficos, calcule correlações, e compare os resultados.

14.7.4 Exemplo: planetas

• A distância média de um planeta ao Sol, em milhões de km, está correlacionada com a posição do planeta na sequência, mas como?

• Gráfico:

  planetas %>% 
    ggplot(aes(posição, distância)) +
      geom_point() +
      scale_x_continuous(breaks = 1:9) +
      labs(
        y = 'distância\n(milhões km)'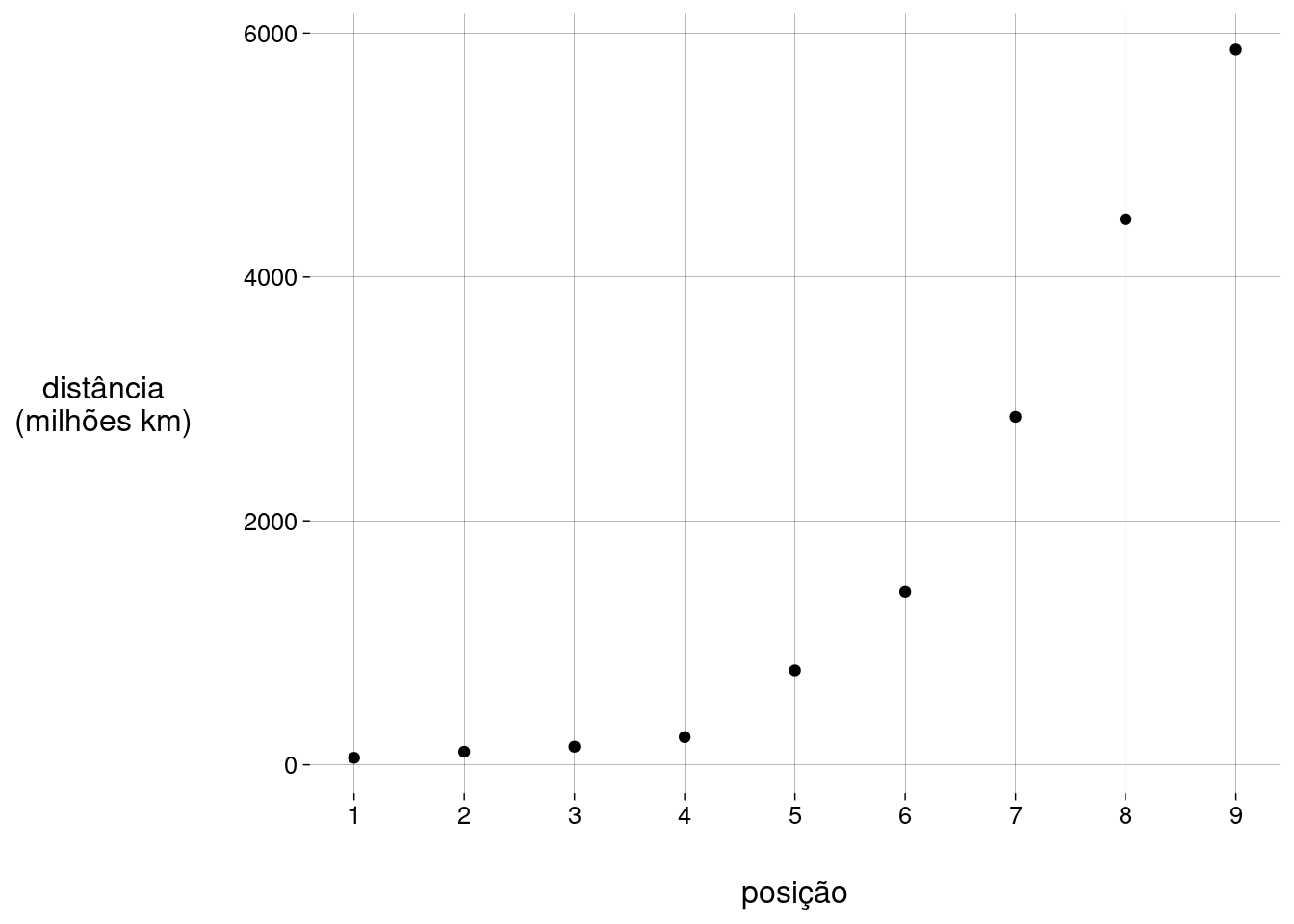
      )

  

• Coeficiente de correlação:

  cor(planetas$posição, planetas$distância)

  ## [1] 0,9102565

• Vamos transformar os valores das distâncias usando \(\log\):

  planetas <- planetas %>% 
    mutate(ldist = log10(distância))

  planetas %>% 
    ggplot(aes(posição, ldist)) +
      geom_point() +
      scale_x_continuous(breaks = 1:9) +
      labs(
        y = 'log distância\n(milhões km)'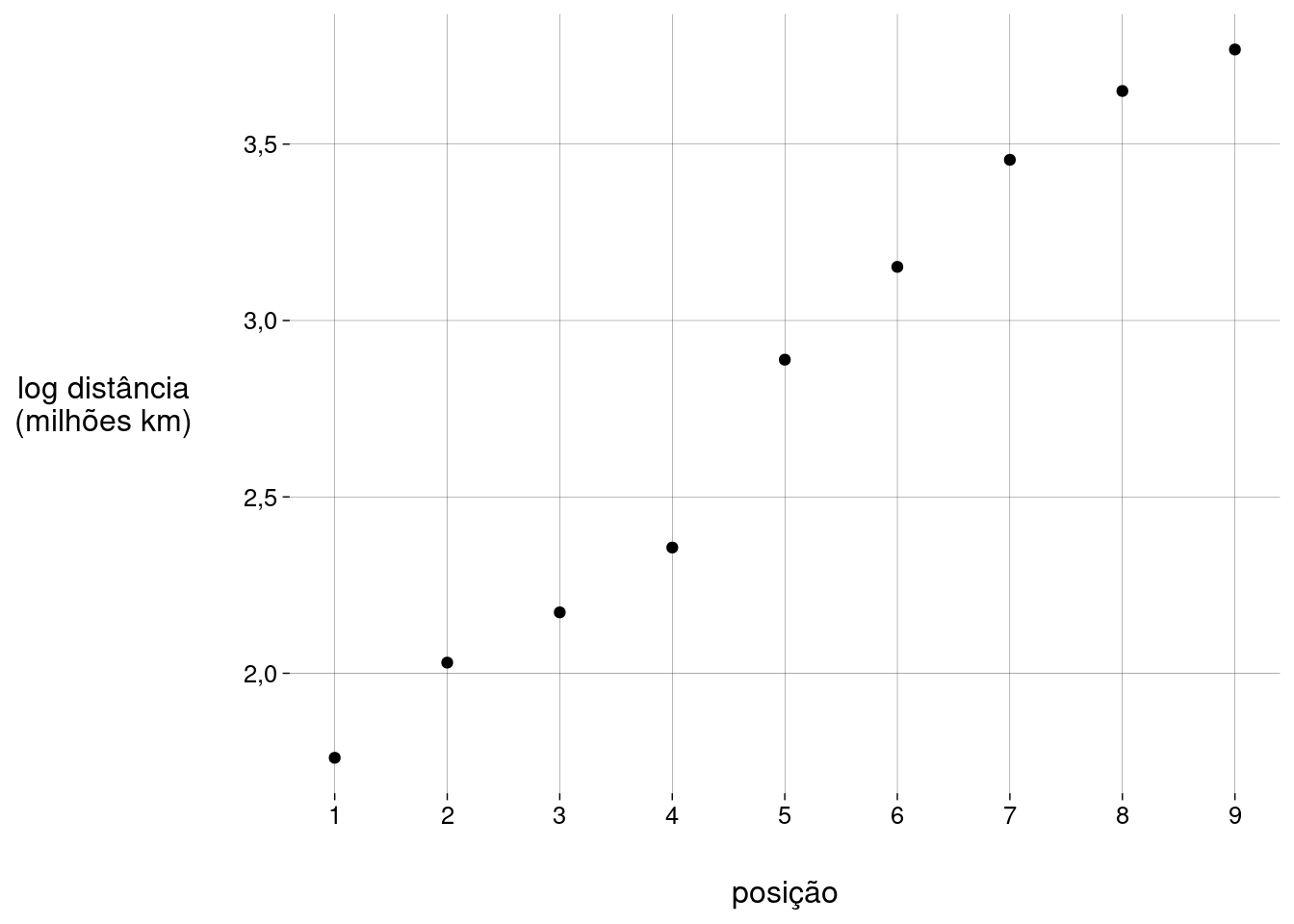
      )

  

• A correlação se torna

  cor(planetas$posição, planetas$ldist)

  ## [1] 0,990712

14.7.5 Exercício

• Aplique as outras transformações da lista acima aos valores da variável distância. Desenhe gráficos, calcule correlações, e compare os resultados.