Capítulo 11 Teorema central do limite

11.1 Vídeo

11.2 Objetivo

Neste capítulo, vamos pensar em todas as amostras possíveis de tamanho \(n\) que podem ser retiradas de uma população.
Se calcularmos a média de cada uma das amostras, teremos um vetor de médias amostrais.
Podemos nos perguntar sobre a distribuição destas médias amostrais:
- Qual é a forma desta distribuição?
- Qual é a média desta distribuição?
- Qual é o desvio-padrão desta distribuição?
Em um experimento, quando coletamos uma amostra de uma população e calculamos a sua média, estamos escolhendo, aleatoriamente, um elemento desta distribuição de médias amostrais.
Podemos considerar a média amostral como uma variável aleatória, cuja distribuição é a distribuição de todas as médias amostrais possíveis.

11.3 Populações não-normais

11.3.1 Uniforme

Vamos começar com um exemplo.
Imagine que temos uma população cujos valores (entre \(0\) e \(1\)) obedecem a uma distribuição uniforme.
```
tamanho_populacao <- 1e5
uniforme <- runif(tamanho_populacao)
```
Vamos retirar amostras (de tamanho \(n\) fixo) desta população e calcular a média de cada amostra.
```
tamanho_amostra <- 100
```

Por exemplo, três amostras e suas respectivas médias:

a1 <- sample(uniforme, tamanho_amostra)
a1

##   [1] 0,869329581 0,209982300 0,496638928 0,499368979 0,186657457 0,344342385
##   [7] 0,116801439 0,189941214 0,772423104 0,778783751 0,093156450 0,047591340
##  [13] 0,899949302 0,226315399 0,552560914 0,525825123 0,029640391 0,561917409
##  [19] 0,559809882 0,859597950 0,804871507 0,146827935 0,058951598 0,280102798
##  [25] 0,285028522 0,519327860 0,433106976 0,333304451 0,476584831 0,954638124
##  [31] 0,780591801 0,101339978 0,314654316 0,990242735 0,844954866 0,967392699
##  [37] 0,405311205 0,171424852 0,213557780 0,055929760 0,622402403 0,135257883
##  [43] 0,290075190 0,202630254 0,594905346 0,901837959 0,236021807 0,759908866
##  [49] 0,113728049 0,299836375 0,761246537 0,939895977 0,143753349 0,440195605
##  [55] 0,819540306 0,645228428 0,774125327 0,687840871 0,914238179 0,447603248
##  [61] 0,193711443 0,703450752 0,631015757 0,495302198 0,729789897 0,950673754
##  [67] 0,571333267 0,932531156 0,021805045 0,393015711 0,560980635 0,593482739
##  [73] 0,435080813 0,404940347 0,863593709 0,845344782 0,248668870 0,745614397
##  [79] 0,500851495 0,714276091 0,571823950 0,664567435 0,483944942 0,451380692
##  [85] 0,974769468 0,182308296 0,618412335 0,784412536 0,429907971 0,524626410
##  [91] 0,839356654 0,009628747 0,982638869 0,460771559 0,447391513 0,701077975
##  [97] 0,419461402 0,022708026 0,071822650 0,268530721

mean(a1)

## [1] 0,5013405

a2 <- sample(uniforme, tamanho_amostra)
a2

##   [1] 0,537127257 0,714157724 0,758129320 0,607783146 0,191654072 0,558148076
##   [7] 0,153129519 0,968886300 0,560464972 0,078813070 0,847052889 0,435220801
##  [13] 0,429718401 0,675571424 0,064212858 0,555145596 0,983912982 0,017477169
##  [19] 0,739916454 0,159267699 0,646231567 0,767586507 0,459140804 0,794855330
##  [25] 0,474957738 0,391580225 0,807984830 0,722808217 0,306649534 0,904464052
##  [31] 0,280691341 0,612927329 0,193282636 0,751671237 0,066252671 0,672371127
##  [37] 0,906193240 0,801269493 0,956015212 0,053552623 0,814222519 0,287908558
##  [43] 0,282878551 0,817179111 0,913337606 0,688490601 0,023302804 0,801148736
##  [49] 0,920262174 0,384750240 0,562533689 0,627294533 0,890178173 0,002385939
##  [55] 0,959085852 0,881101963 0,070349924 0,324673084 0,567032631 0,483372909
##  [61] 0,779220516 0,059368621 0,608695943 0,664166924 0,870103676 0,590112060
##  [67] 0,815081495 0,359841079 0,455165238 0,727277773 0,940016040 0,687818256
##  [73] 0,521265980 0,804189556 0,699634301 0,712968478 0,941152321 0,136708336
##  [79] 0,891254095 0,377979213 0,835787549 0,257772818 0,895569389 0,506121808
##  [85] 0,633335854 0,540881501 0,690710838 0,014458583 0,677491209 0,612267448
##  [91] 0,941688599 0,347645721 0,032504889 0,003996033 0,697600042 0,229145339
##  [97] 0,873270965 0,310203195 0,757048784 0,455766988

mean(a2)

## [1] 0,5586305

a3 <- sample(uniforme, tamanho_amostra)
a3

##   [1] 0,37304029 0,60533056 0,67742812 0,78079738 0,16619780 0,80176380 0,84082814
##   [8] 0,75545430 0,34654105 0,66697578 0,87747161 0,56437873 0,22576855 0,52757542
##  [15] 0,15433794 0,07798435 0,03805315 0,84833770 0,68201463 0,88777552 0,05874217
##  [22] 0,53917469 0,06612466 0,52500553 0,82302671 0,30956999 0,99802753 0,48249254
##  [29] 0,16667167 0,71622572 0,77946385 0,15810985 0,96864575 0,85040020 0,94900362
##  [36] 0,95843226 0,04596898 0,52233577 0,55952978 0,75270363 0,71364222 0,49835529
##  [43] 0,50404666 0,10957463 0,14820706 0,90270814 0,12726159 0,93155567 0,02479344
##  [50] 0,21812856 0,50801571 0,57523798 0,93646581 0,56547527 0,25987711 0,95085959
##  [57] 0,05043098 0,46683682 0,51838925 0,06147510 0,19338896 0,99457904 0,76212994
##  [64] 0,67796055 0,36979235 0,86383912 0,64535102 0,92774725 0,63143062 0,80798963
##  [71] 0,48495490 0,46092112 0,22269385 0,34606527 0,83653930 0,85864444 0,31877899
##  [78] 0,24316776 0,76869982 0,47943708 0,63683160 0,57907865 0,29393781 0,39491851
##  [85] 0,36160928 0,03643693 0,38048180 0,43833383 0,31232725 0,81037264 0,43365283
##  [92] 0,54855347 0,25296780 0,06554264 0,33923681 0,90978174 0,54939680 0,36144745
##  [99] 0,05036426 0,55322867

mean(a3)

## [1] 0,5140166

Teremos, então, um conjunto de médias amostrais.

medias <- c(mean(a1), mean(a2), mean(a3))
medias

## [1] 0,5013405 0,5586305 0,5140166

Qual é a média destas médias amostrais?
```
mean(medias)
```
```
## [1] 0,5246626
```
Qual é o desvio-padrão destas médias amostrais?
```
sd(medias)
```
```
## [1] 0,03009216
```

Vamos ver as respostas para um exemplo maior: \(10.000\) amostras de \(100\) elementos cada:

## Média da população         = 0,499
## desvio-padrão da população = 0,288
## 
## Quantidade de amostras     = 10000
## Tamanho da amostra         = 100
## 
## Média das médias amostrais = 0,499
## D.P. das médias amostrais  = 0,029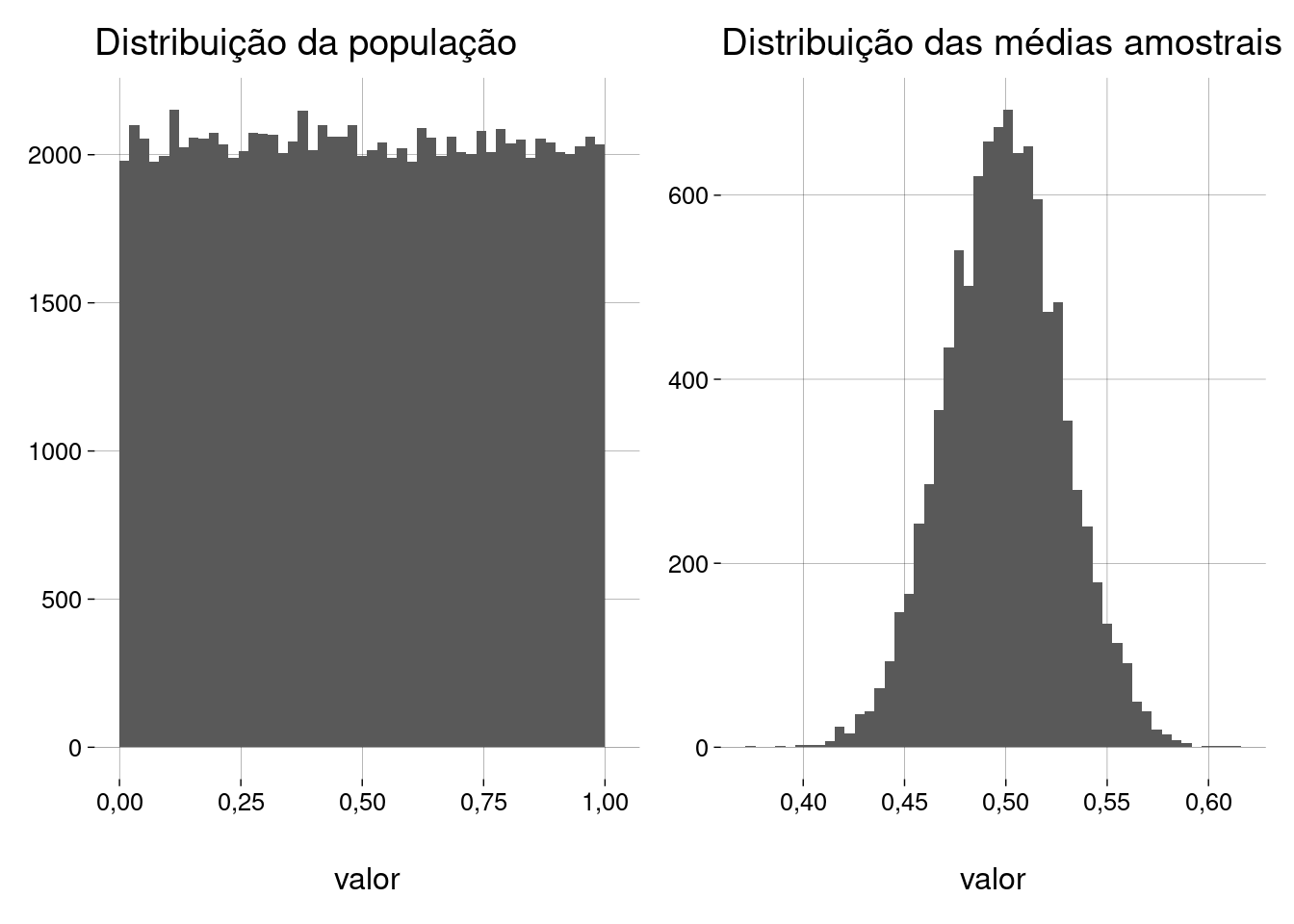

A distribuição da população é uniforme, mas a distribuição das médias amostrais parece normal!
A média das médias amostrais é próxima da média populacional.
E o desvio-padrão das médias amostrais é função do desvio-padrão da população. Na verdade, este desvio-padrão é

\[ \frac{\sigma}{\sqrt{100}} \]

onde \(\sigma = 0{,}29\) é o desvio-padrão da população, e \(100\) é o tamanho de cada amostra.

Terminologia

A distribuição das médias amostrais (o gráfico à direita no exemplo acima) é chamada de distribuição amostral das médias.
O desvio-padrão da distribuição amostral é chamado de erro-padrão, embora não haja uma idéia clara de erro aqui.
A média de todas as médias amostrais é a média populacional. Por incrível que pareça, fica mais fácil entender isto quando escrevemos em matemática:

\[ E(\overline X) = \mu \]
Chamamos \(\overline X\) de um estimador não-tendencioso (unbiased, ou não-enviesado) de \(\mu\).

11.3.2 Exponencial

Agora, vamos fazer um exemplo com uma população com distribuição exponencial:
```
tamanho_populacao <- 1e5
tamanho_amostra <- 100
qtde_amostras <- 1e4
```

Definimos a população com \(\lambda = 2\):

exponencial <- rexp(tamanho_populacao, 2)

Vamos retirar muitas amostras e examinar os resultados:

## Média da população         = 0,5
## desvio-padrão da população = 0,499
## 
## Quantidade de amostras     = 10000
## Tamanho da amostra         = 100
## 
## Média das médias amostrais = 0,501
## D.P. das médias amostrais  = 0,05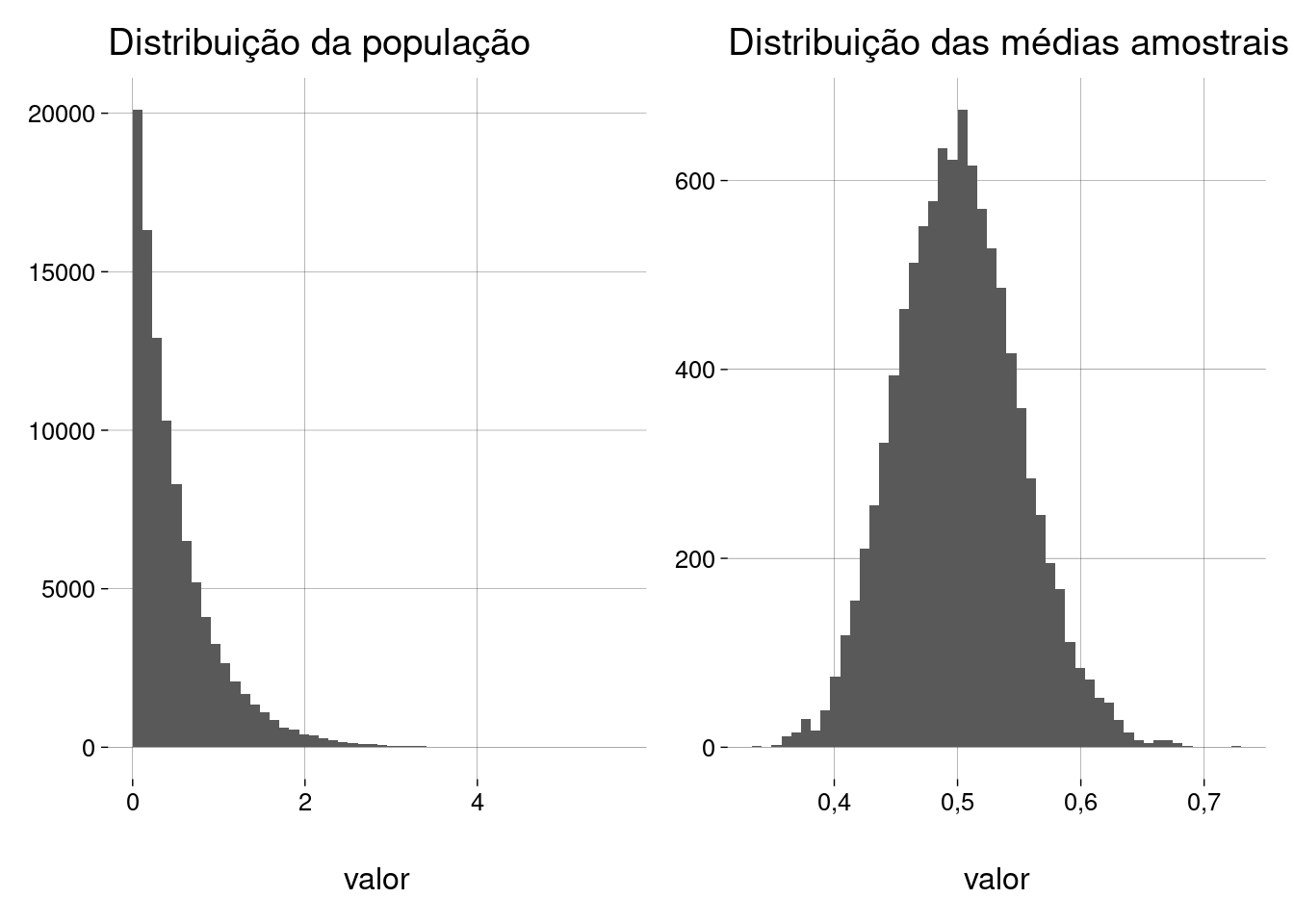

De novo, a distribuição das médias amostrais é normal, com média igual à média da população original.

11.3.3 Uma mistura

Agora, uma população que é uma mistura de uma binomial com uma Poisson:

tamanho_populacao <- 1e5
tamanho_amostra <- 100
qtde_amostras <- 1e4

mistura <- c(
  rbinom(tamanho_populacao/2, size = 10, prob = .3),
  rpois(tamanho_populacao/2, lambda = 15)
)

Vamos retirar muitas amostras e examinar os resultados:

## Média da população         = 8,998
## desvio-padrão da população = 6,667
## 
## Quantidade de amostras     = 10000
## Tamanho da amostra         = 100
## 
## Média das médias amostrais = 9,002
## D.P. das médias amostrais  = 0,678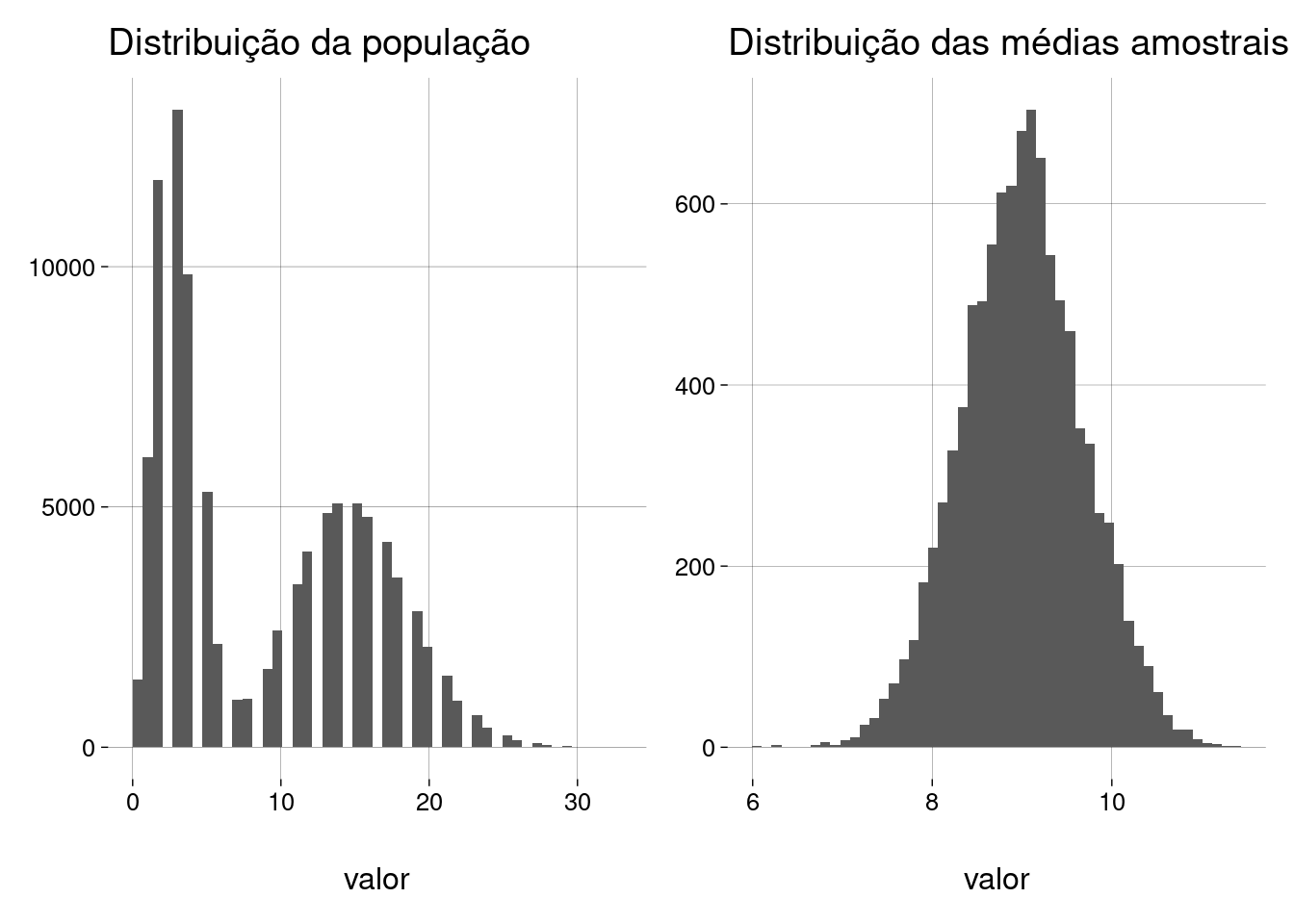

Observe que, embora a população tenha uma distribuição discreta, a distribuição das médias amostrais é sempre contínua.
De novo, a distribuição das médias amostrais é normal, com média igual à média da população original.

11.4 Uma população normal

E se a população já for distribuída normalmente?

Definimos uma população normal padrão (\(\mu = 0, \sigma = 1\)):

tamanho_populacao <- 1e5
tamanho_amostra <- 100
qtde_amostras <- 1e4

normal <- rnorm(tamanho_populacao)

Vamos retirar muitas amostras e examinar os resultados:

## Média da população         = 0
## desvio-padrão da população = 1,003
## 
## Quantidade de amostras     = 10000
## Tamanho da amostra         = 100
## 
## Média das médias amostrais = 0
## D.P. das médias amostrais  = 0,1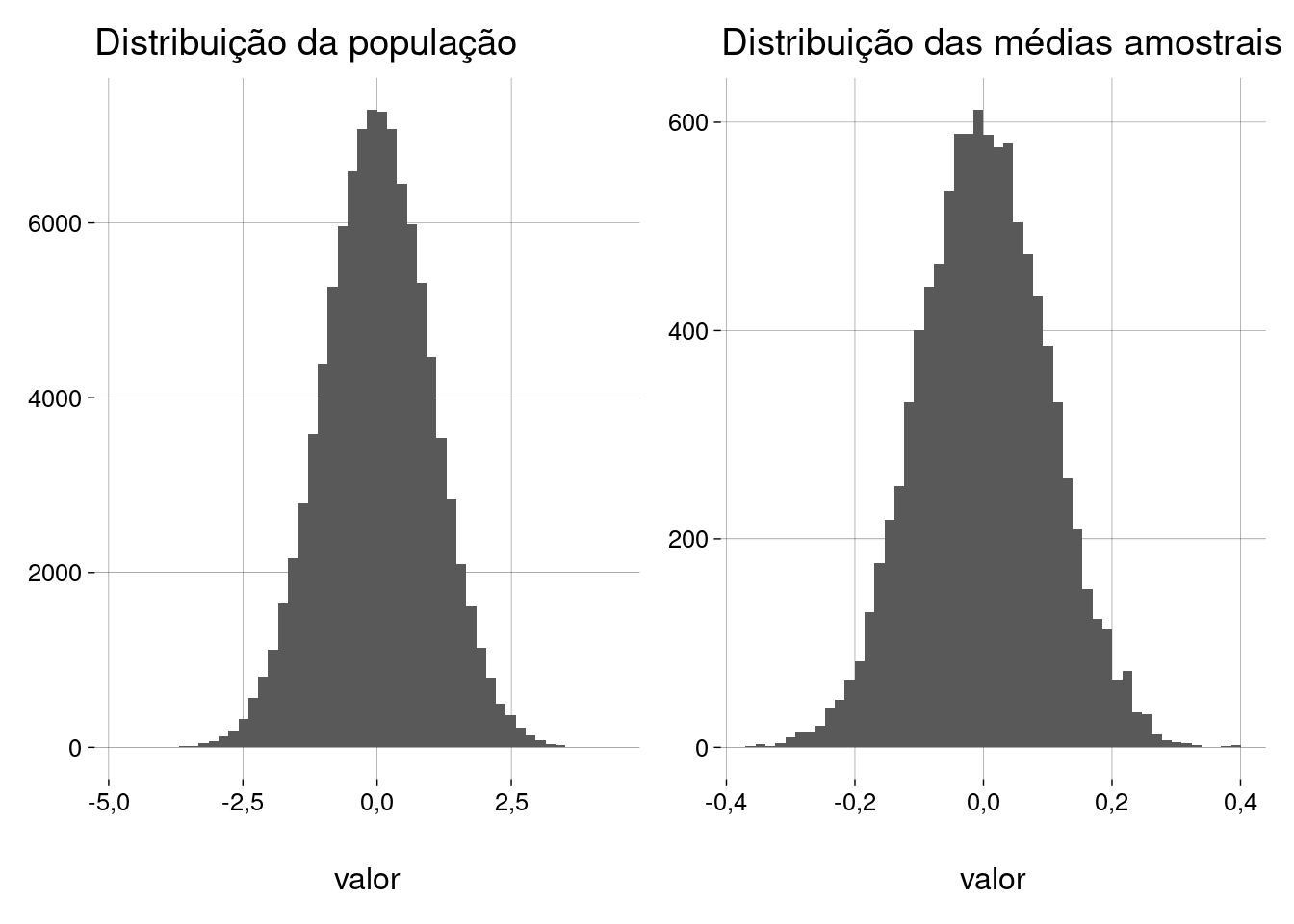

11.5 O que isto significa? O TCL

Em primeiro lugar, que a distribuição normal é mágica! Tão mágica que seu nome deveria ser outro:

Em segundo lugar, que é possível provar o

Teorema Central do Limite (TCL)

Pense em uma população com distribuição qualquer, com média \(\mu\) e desvio-padrão \(\sigma\) (\(\mu\) e \(\sigma\) finitos).
Pense em todas as amostras de tamanho \(n\) possíveis, retiradas desta população.
As médias de todas estas amostras são valores de uma variável aleatória \(\overline X\), e podemos dizer que, quanto maior o valor de \(n\):
- Mais próxima da distribuição normal é a distribuição de \(\overline X\).
- Mais próximo de \(\mu\) é o valor esperado \(E(\overline X)\).
- Mais próximo de \(\frac{\sigma}{\sqrt{n}}\) é o desvio-padrão de \(\overline X\).
Note que o desvio-padrão da distribuição das médias amostrais (i.e., o erro-padrão)
- Aumenta quando o tamanho da amostra \(n\) diminui.
- Diminui quando o tamanho da amostra \(n\) aumenta.

11.5.1 Prova do TCL (parcial)

Não vamos provar que a distribuição de \(\overline X\) é normal — precisamos de funções geradoras de momentos, um assunto de estatística matemática que não vamos cobrir aqui.
Mas é fácil provar que \(E(\overline X) = \mu\):
- A média amostral \(\overline X\) é uma variável aleatória que é a soma de \(n\) variáveis aleatórias \(X_1, X_2, \ldots, X_n\) (que representam os elementos de cada amostra) dividida pelo tamanho da amostra, \(n\).
- Mais precisamente
  
  \[ \overline X = \frac{X_1 + X_2 + \cdots + X_n}{n} \]
- Cada uma destas variáveis \(X_i\) tem valor esperado \(\mu\) (porque cada uma delas vem da população, que tem média \(\mu\)).
- Em um vídeo anterior, vimos que o valor esperado de uma soma de variáveis aleatórias é a soma dos valores esperados.
- Vimos também que multiplicar a variável por uma constante (\(\frac1n\), aqui) multiplica o valor esperado pela mesma constante.
- Então
  
  \[ \begin{align*} E(\overline X) &= E \left(\frac{X_1 + X_2 + \cdots + X_n}{n} \right) \\ &= \frac1n \cdot E(X_1 + X_2 + \cdots + X_n) \\ &= \frac1n \cdot [E(X_1) + E(X_2) + \cdots + E(X_n)] \\ &= \frac1n \cdot [\mu + \mu + \cdots + \mu] \\ &= \frac1n \cdot n \cdot \mu \\ &= \mu \end{align*} \]
Também é fácil provar que o desvio-padrão de \(\overline X\) é \(\frac{\sigma}{\sqrt{n}}\):
- Vamos pensar sobre a variância.
- Cada uma destas variáveis \(X_i\) tem variância \(\sigma^2\) (porque cada uma delas vem da população, que tem variância \(\sigma^2\)).
- A variância da soma de variáveis aleatórias independentes é a soma das variâncias.
- Multiplicar a variável por uma constante (\(\frac1n\), aqui) multiplica a variância pelo quadrado da constante (\(\frac1{n^2}\)).
- Então:
  
  \[ \begin{align*} \text{Var}(\overline X) &= \text{Var}\left(\frac{X_1 + X_2 + \cdots + X_n}{n} \right) \\ &= \frac1{n^2} \cdot \text{Var}(X_1 + X_2 + \cdots + X_n) \\ &= \frac1{n^2} \cdot [\text{Var}(X_1) + \text{Var}(X_2) + \cdots + \text{Var}(X_n)] \\ &= \frac1{n^2} \cdot [\sigma^2 + \sigma^2 + \cdots + \sigma^2] \\ &= \frac1{n^2} \cdot n \cdot \sigma^2 \\ &= \frac{\sigma^2}{n} \end{align*} \]
- Como o desvio-padrão é a raiz quadrada da variância, o desvio-padrão de \(\overline X\) é \(\sqrt{\frac{\sigma^2}{n}} = \frac{\sigma}{\sqrt{n}}\), onde \(\sigma\) é o desvio-padrão da população.

11.6 Proporções

O TCL fala de médias, mas também serve para proporções.
Exemplo: de uma população de \(1.000\) pessoas, você extrai uma amostra de \(100\) pessoas e calcula a proporção \(\hat p\) de fumantes na amostra. O que o TCL diz sobre \(\hat p\)?
\(\hat p\) é o número \(k\) de fumantes na amostra, dividido pelo tamanho da amostra \(n\):

\[ \hat p = \frac kn \]
Mas isto também pode ser calculado da seguinte forma:
1. Represente cada pessoa da amostra por \(0\) ou por \(1\), dependendo de se ela é não-fumante ou fumante, respectivamente. Isto equivale a definir \(n\) variáveis aleatórias \(X_1, X_2, \ldots, X_n\), tais que
  
  \[ X_i = \begin{cases} 0 & \text{se a pessoa } i \text{ é não-fumante}\\ 1 & \text{se a pessoa } i \text{ é fumante} \end{cases} \]
  
  Em R, guarde todos estes \(0\)s e \(1\)s em um vetor X.
2. O número de fumantes na amostra vai ser \(\sum X_i\), ou, em R, sum(X).
3. Se você dividir esta soma por \(n\), você terá a média das variáveis \(X_i\), que é exatamente a proporção de fumantes na amostra. Em R, mean(X).
  
  \[ \hat p = \frac{\sum X_i}{n} \]
4. Conclusão: a proporção também é uma média, e também obedece ao TCL.
O TCL diz que a distribuição amostral de \(\hat p\) é normal.
O TCL diz que o valor esperado de \(\hat p\) é a proporção \(p\) de fumantes na população. Ou seja, se você retirar muitas amostras de \(n\) pessoas, com \(n\) suficientemente grande, a média das proporções amostrais vai ser a proporção populacional.

\[ E(\hat p) = p \]

Usando a terminologia que já vimos, \(\hat p\) é um estimador não-tendencioso de \(p\).
Para calcular o desvio-padrão, pense que uma proporção tem tudo a ver com uma variável aleatória binomial \(Y\), cujo valor é o número de fumantes (sucessos) em uma amostra de \(n\) pessoas (\(n\) provas de Bernoulli), onde cada pessoa tem probabilidade \(\hat p\) de ser fumante (\(\hat p\) é a proporção de fumantes na amostra).
Por este raciocínio, a proporção amostral é \(\frac Yn\).
Da aula sobre variáveis aleatórias discretas, você lembra que \(Y\) tem variância \(n\hat p (1 - \hat p)\) e, daí, desvio-padrão \(\sqrt{\hat p (1 - \hat p)}\).
O TCL diz que o desvio-padrão da distribuição amostral de \(\hat p\) vai ser

\[ \frac{\sqrt{\hat p (1 - \hat p)}}{\sqrt{n}} \quad=\quad \sqrt{\frac{\hat p (1 - \hat p)}{n}} \]

Vamos fazer uma simulação:

tamanho_populacao <- 1e3
tamanho_amostra <- 100
qtde_amostras <- 1e4
proporcao_pop <- .3

populacao <- sample(
  0:1, 
  tamanho_populacao, 
  replace = TRUE, 
  prob = c(1 - proporcao_pop, proporcao_pop)
)

## Média da população         = 0,307
## desvio-padrão da população = 0,461
## 
## Quantidade de amostras     = 10000
## Tamanho da amostra         = 100
## 
## Média das médias amostrais = 0,307
## D.P. das médias amostrais  = 0,043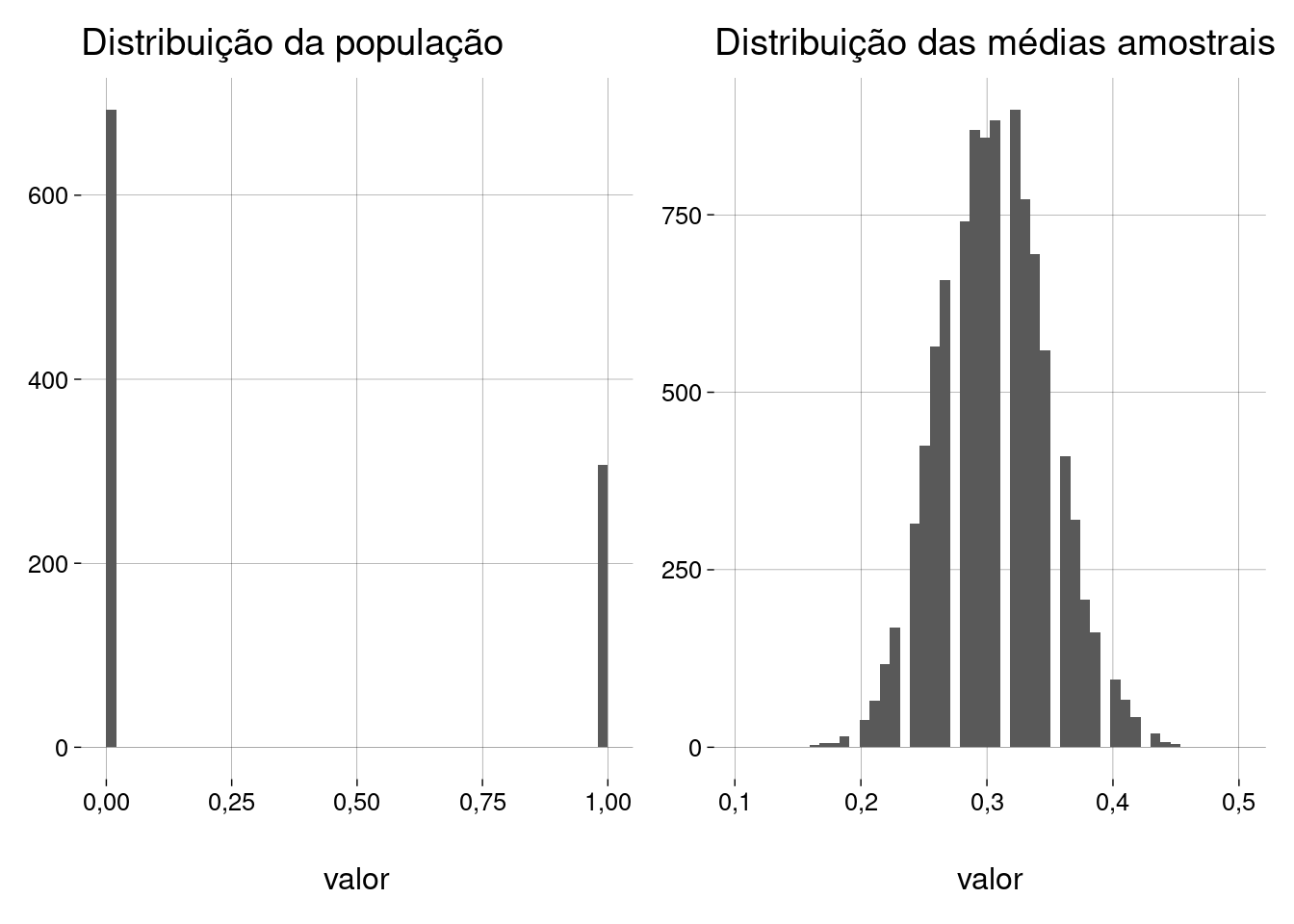

11.7 Condições para usar o TCL na prática

Quando você obtém uma amostra de uma população, você deve observar as seguintes condições:

O tamanho \(n\) da amostra deve ser grande o bastante. Na prática, \(n \geq 30\) é razoável.
Quando a amostra vem de uma população com distribuição normal, o tamanho da amostra pode ser menor (\(n \geq 10\)).
Os indivíduos da amostra devem ser independentes entre si. Na teoria, a população deveria ser infinita, e as amostras, aleatórias.
- Na prática, basta a população ser grande o bastante em relação ao tamanho da amostra. Geralmente, \(n\) não deve ultrapassar \(10\%\) do tamanho da população.
- Na prática, quanto mais randomizada for a amostra, melhor.
No caso de proporções, uma amostra com uma quantidade potencial muito grande ou muito pequena de sucessos vai acabar gerando uma distribuição amostral não-normal. Na prática, sua amostra deve ter, potencialmente, pelo menos \(10\) sucessos e pelo menos \(10\) fracassos.

11.8 Mais exemplos

Adaptados de De Veaux, Velleman, e Bock (2016).

11.8.1 Canhotos

Suponha que \(13\%\) da população sejam de pessoas canhotas.
Uma sala de aula tem \(200\) carteiras, com \(15\) carteiras especiais para alunos canhotos.
Em uma turma de \(90\) alunos, qual a probabilidade de que estas carteiras especiais não sejam suficientes para os alunos canhotos?

Resposta

A pergunta é: em uma amostra com \(n = 90\) alunos, qual a probabilidade de haver mais de \(15\) alunos canhotos?
Traduzindo para proporção: qual a probabilidade de \(\hat p\) (a proporção de canhotos na amostra) ser maior que \(\frac{15}{90} = 0{,}167\)?
Ou seja, queremos achar \(P(\hat p > 0{,}167)\).
A proporção populacional \(p\) é \(0{,}13\).
Vamos verificar as condições para usar o TCL:
1. O tamanho da amostra é grande o bastante? Sim, \(n = 90\).
2. O tamanho da amostra é menos que \(10\%\) da população? Ninguém nos disse qual é a população. Vamos supor que a população é o conjunto de todos os alunos da cidade, e que a cidade tem mais de \(900\) alunos; então esta condição está satisfeita.
3. Os indivíduos são independentes entre si? Podemos supor que sim: um aluno ser canhoto não afeta a probabilidade de outro aluno ser canhoto (a não ser que se trate de uma escola especial para canhotos ou que todos os alunos sejam clones).
4. A amostra é aleatória? Só podemos responder se soubermos como os \(90\) alunos foram escolhidos. Vamos supor que sim.
5. Existem potencialmente mais de \(10\) sucessos e mais de \(10\) fracassos na amostra? Sim, potencialmente, são \(90 \cdot 0{,}13 = 11{,}7\) canhotos e \(90 \cdot 0{,}87 = 78{,}3\) destros.
A distribuição amostral de \(\hat p\), segundo o TCL, vai ser a normal com média

\[ p = 0{,}13 \]

e erro-padrão (lembre-se de que este é o nome do desvio-padrão da distribuição amostral)

\[ \sqrt{\frac{p(1-p)}{n}} \quad=\quad \sqrt{\frac{0{,}13\cdot 0{,}87}{90}} \quad\approx\quad 0{,}035 \]
Ou seja, \(\hat p \sim \mathcal N (0{,}13; 0{,}035)\), e nós queremos \(P(\hat p > 0{,}167)\). Basta usar o R:
```
pnorm(q = .167, mean = .13, sd = .035, lower.tail = FALSE)
```
```
## [1] 0,1452232
```
Conclusão: existe uma chance de aproximadamente \(14{,}5\%\) de que as carteiras especiais para canhotos não sejam suficientes para uma turma de \(90\) alunos.
E se a turma for de \(200\) alunos, lotando a sala?

11.8.2 Elevador

O peso de um homem adulto é distribuído normalmente, com média de \(86\)kg e desvio-padrão de \(26{,}8\)kg.
O limite de peso de um elevador é de \(10\) pessoas ou \(1.100\)kg.
Qual a probabilidade de que \(10\) homens entrem no elevador e excedam o limite de peso?

Resposta

Para os \(10\) homens excederem o limite de peso, o total dos seus pesos deve ultrapassar \(1.100\)kg, o que equivale a dizer que o peso médio deve ultrapassar \(1.100 / 10 = 110\)kg.
A pergunta, então, é: qual a probabilidade \(P(\overline X \geq 110)\)?
Vamos verificar as condições para usar o TCL:
1. O tamanho da amostra é grande o bastante? Como, na população, o peso tem distribuição normal, \(n = 10\) está OK.
2. O tamanho da amostra é menos que \(10\%\) da população? De novo, ninguém nos disse qual é a população. Vamos supor que a população é o conjunto de todos os homens da cidade. Então, \(n = 10\) é menos do que \(10\%\) da população.
3. Os indivíduos são independentes entre si? Podemos supor que sim. Os homens não são todos parentes, não são todos faquires, nem são todos lutadores de sumô.
4. A amostra é aleatória? Vamos supor que sim. O elevador não está numa clínica de emagrecimento. O conjunto de homens é escolhido ao acaso na população geral.
A distribuição amostral de \(\overline X\), segundo o TCL, vai ser a normal com média

\[ \mu = 86 \]

e erro-padrão (lembre-se de que este é o nome do desvio-padrão da distribuição amostral)

\[ \frac{\sigma}{\sqrt{n}} \quad=\quad \frac{26{,}8}{\sqrt{10}} \quad\approx\quad 8{,}47 \]
Ou seja, \(\overline X \sim \mathcal N (86; 8{,}47)\), e nós queremos \(P(\overline X \geq 110)\). Basta usar o R:
```
pnorm(q = 110, mean = 86, sd = 8.47, lower.tail = FALSE)
```
```
## [1] 0,002301849
```
Conclusão: existe uma probabilidade muito pequena — \(0{,}2\%\) — de que uma amostra de \(10\) homens exceda o limite de peso do elevador.

10 Distribuições contínuas

12 Intervalos de confiança