Capítulo 8 Variáveis aleatórias

8.1 Vídeo

8.2 O que é uma variável aleatória?

Uma variável aleatória é uma maneira de associar a cada resultado do espaço amostral um número real.
Dependendo do conjunto de números, a variável aleatória pode ser discreta ou contínua.
Falamos sobre a probabilidade de uma variável aleatória assumir um valor (ou uma faixa de valores).

8.3 Exemplos

8.3.1 Lançar dois dados

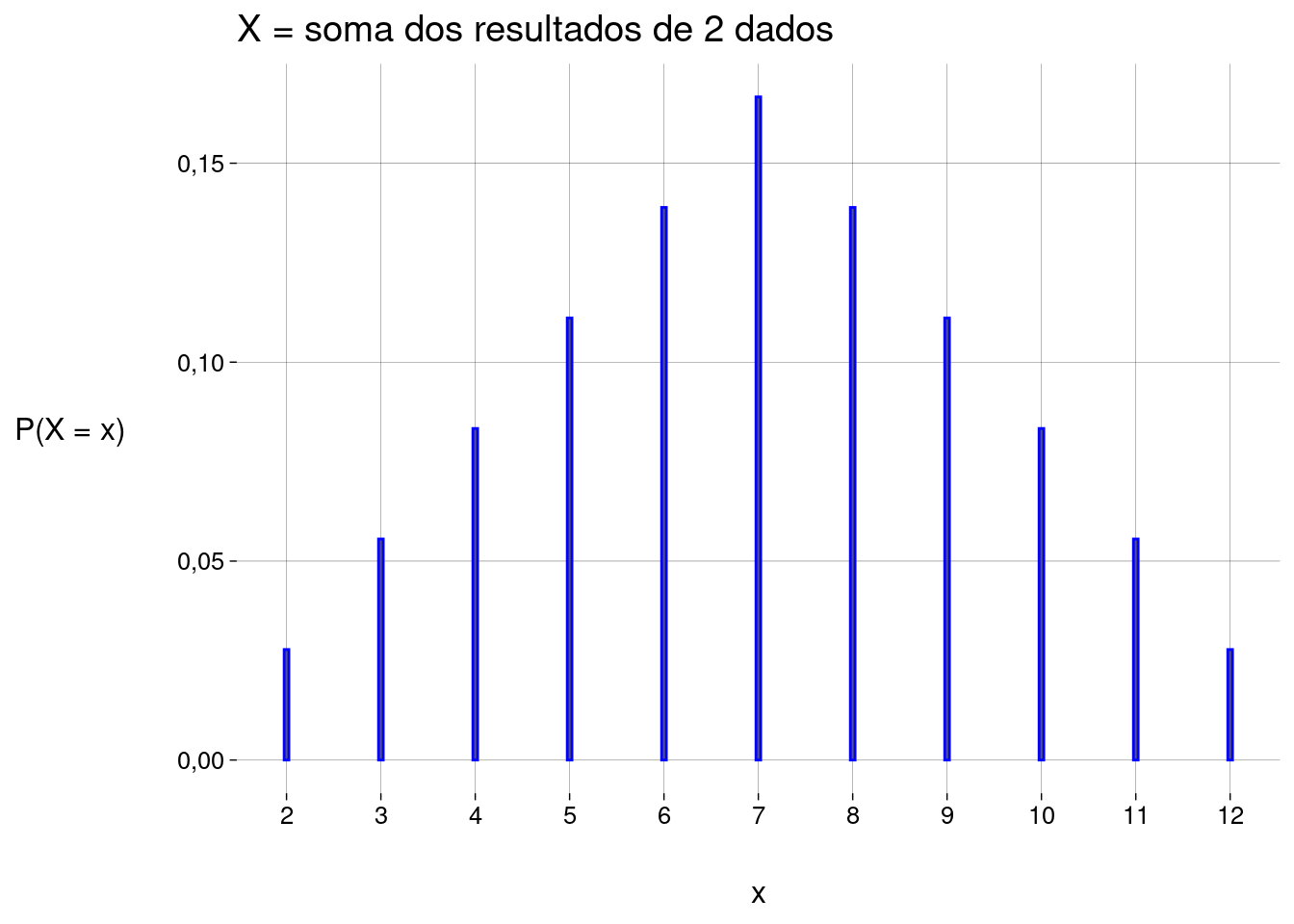
Definimos $X = \text{soma dos resultados dos dois dados}$.
Esta é uma variável aleatória discreta, com $11$ valores possíveis.
A tabela com todos os valores possíveis de $X$ e suas probabilidades é chamada de distribuição de probabilidade:

x	P(X = x)
2	1/36
3	2/36
4	3/36
5	4/36
6	5/36
7	6/36
8	5/36
9	4/36
10	3/36
11	2/36
12	1/36

Graficamente:

Suponha que a distribuição de probabilidade de $X$ esteja na seguinte tibble:

glimpse(dados_distr)

## Rows: 11
## Columns: 3
## $ x          <int> 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
## $ `P(X = x)` <chr> "1/36", "2/36", "3/36", "4/36", "5/36", "6/36", "5/36", "4/36", …
## $ num        <dbl> 0,02777778, 0,05555556, 0,08333333, 0,11111111, 0,13888889, 0,16…

A coluna num tem os valores numéricos das probabilidades.

Qual a probabilidade de conseguir $10$ ou mais?

Basta somar as probabilidades de $X=10$, $X=11$ e $X=12$:
```
dados_distr %>% 
  filter(x >= 10) %>% 
  pull(num) %>% 
  sum()
```
```
## [1] 0,1666667
```

Qual a probabilidade de conseguir entre $6$ e $8$, inclusive?

dados_distr %>% 
  filter(x >= 6 & x <= 8) %>% 
  pull() %>% 
  sum()

## [1] 0,4444444

8.3.2 Altura de um homem adulto

Definimos $X = \text{estatura em metros de um homem brasileiro adulto, escolhido ao acaso}$.
Esta é uma variável aleatória contínua, com um número infinito não-enumerável de valores.
Segundo o Levantamento do Perfil Antropométrico da População Brasileira Usuária do Transporte Aéreo Nacional, em $2009$, a estatura média do homem brasileiro adulto era de $1{,}73$m, com desvio-padrão de $0{,}07$m.

Vamos simular uma amostra de muitos homens desta população:

media <- 1.73
desvio <- 0.07
homens <- tibble(
  altura = rnorm(1e5, mean = media, sd = desvio)
)

Eis um histograma com as percentagens:

homens_plot <- homens %>% 
  ggplot(aes(x = altura)) +
    geom_histogram(
      aes(y = after_stat(density)),
      breaks = seq(1.4, 2, 0.01)
    ) +
    scale_x_continuous(breaks = seq(1.4, 2.0, .1)) +
    labs(
      title = 'Altura de um homem brasileiro adulto',
      x = 'metros',
      y = '%'
    )

homens_plot

Agora, sobrepomos o gráfico de uma distribuição normal com a mesma média e o mesmo desvio-padrão que a distribuição das alturas:

homens_normal <- homens_plot +
  stat_function(
    fun = dnorm, 
    args = list(
      'mean' = media,
      'sd' = desvio
    ),
    geom = 'line',
    color = 'red',
    linewidth = 1
  ) +
  labs(
    subtitle = paste0('com N(', media, ', ', desvio,') em vermelho')
  )

homens_normal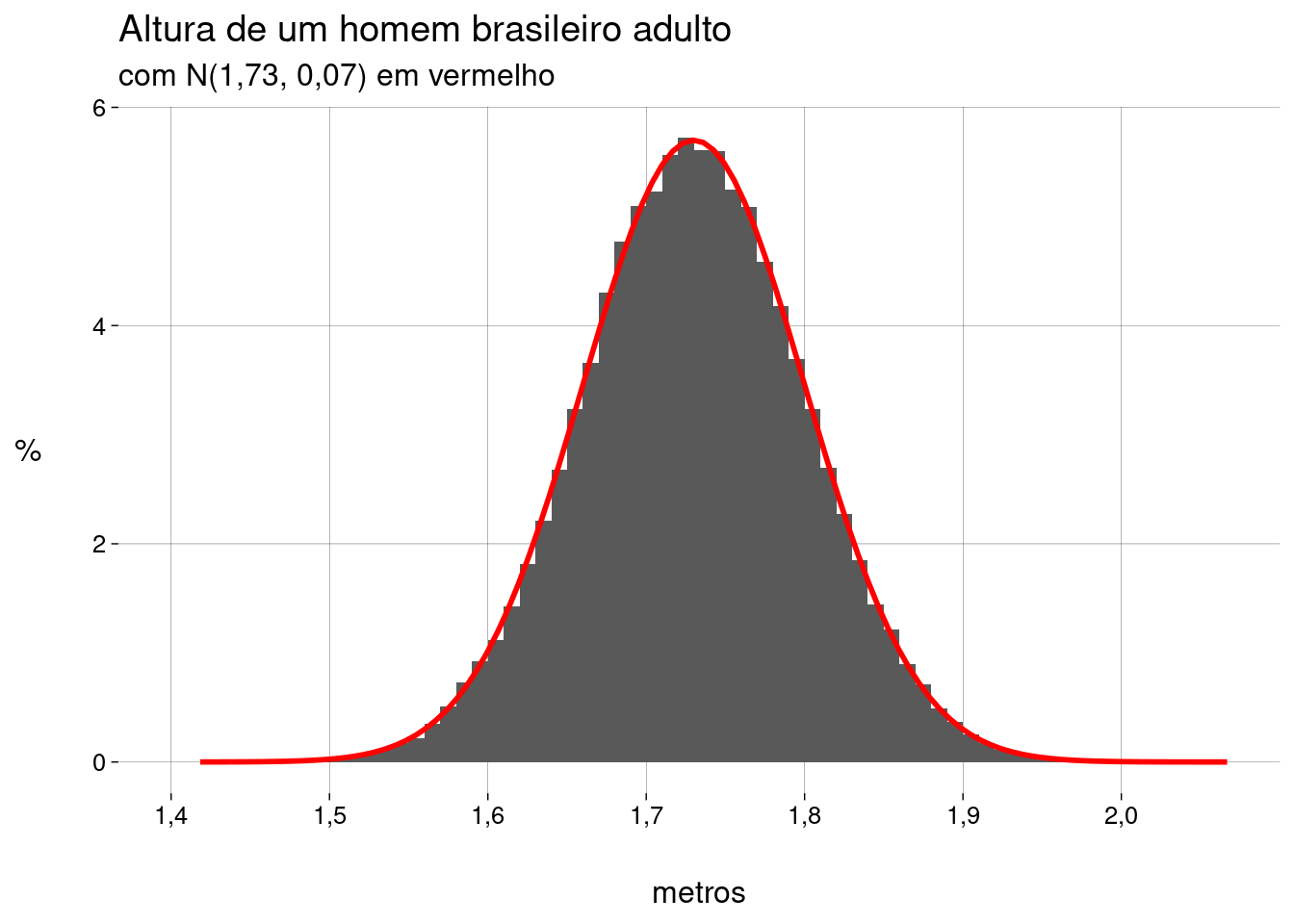

A curva vermelha no gráfico é a função de densidade de probabilidade da distribuição normal, dada por

\[ \text{fdp}(x) = {\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}} \]

Em uma distribuição contínua, não faz sentido perguntar o valor de $P(X = x)$. Como $X$ pode assumir uma quantidade infinita não-enumerável de valores, esta probabilidade é igual a zero!

Com uma distribuição contínua, vamos sempre perguntar sobre faixas de valores.

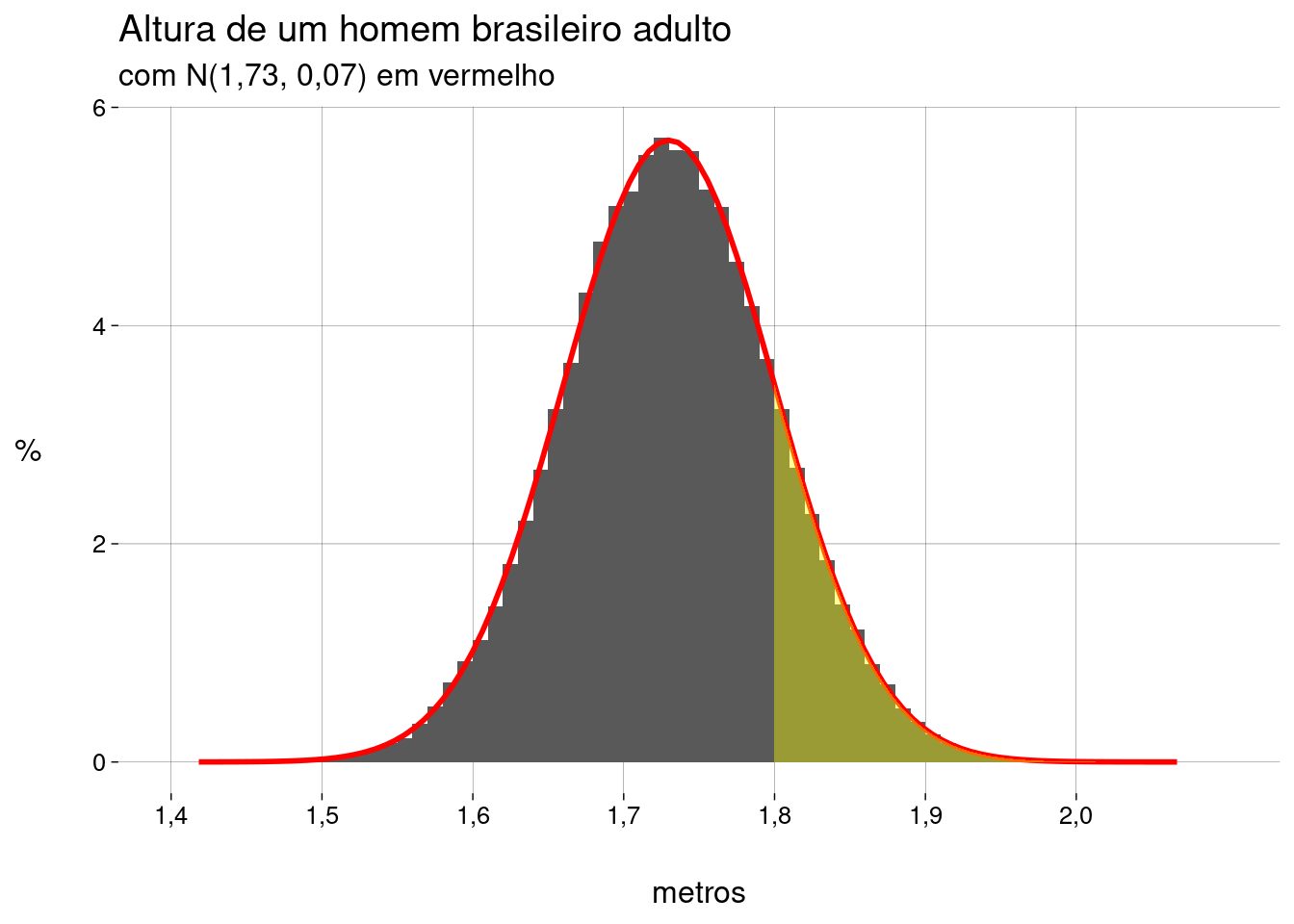
Qual a probabilidade de um homem ter mais de $1{,}80$m?

Na amostra:

mean(homens$altura > 1.80)

## [1] 0,15931

Na distribuição teórica:

pnorm(1.80, mean = media, sd = desvio, lower.tail = FALSE)

## [1] 0,1586553

No gráfico:

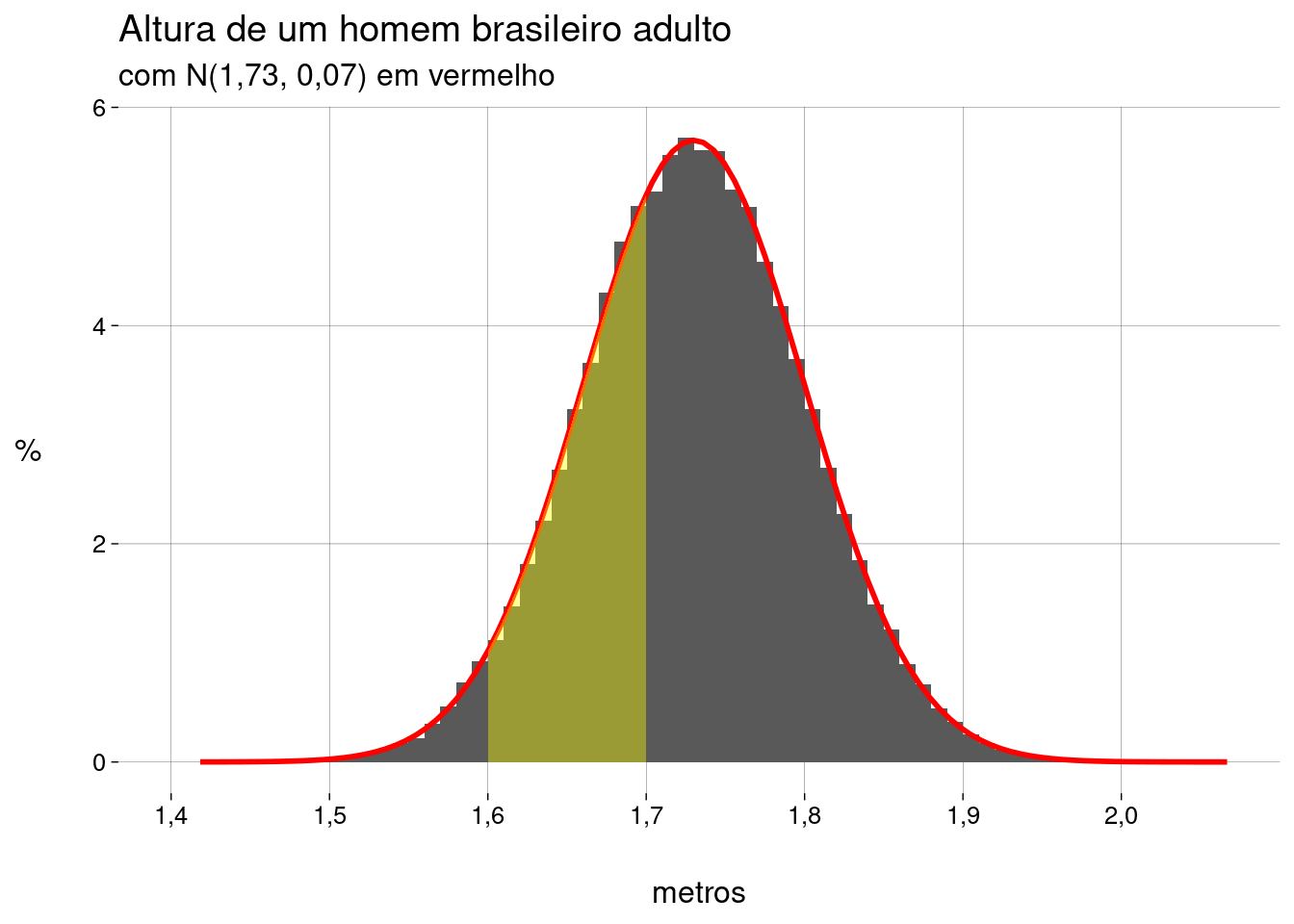
Qual a probabilidade de um homem ter entre $1{,}60$m e $1{,}70$m?

Na amostra:

mean(homens$altura > 1.60 & homens$altura < 1.70)

## [1] 0,30314

Na distribuição teórica:

pnorm(1.70, mean = media, sd = desvio) -
pnorm(1.60, mean = media, sd = desvio)

## [1] 0,3024722

No gráfico:

8.4 Valor esperado

O valor esperado (ou esperança matemática) de uma variável aleatória é a média ponderada dos valores possíveis da variável, considerando as probabilidades (ou, no caso contínuo, a densidade de probabilidade) como pesos.
No caso discreto:

\[ \mu = E(X) = \sum_i x_i \cdot P(X = x_i) \]
No caso contínuo:

\[ \mu = E(X) = \int_{-\infty}^{+\infty} x \cdot \text{fdp}(x) \text{d}x \]

8.4.1 Lançar dois dados

Lembrando que a tibble dados_distr contém a distribuição de probabilidades do valor da soma de dois dados, o valor esperado é
```
dados_distr %>% 
  summarize(E = sum(x * num)) %>% 
  pull(E)
```
```
## [1] 7
```

8.4.2 Lançar um dado

O valor esperado do valor obtido em um lançamento de um dado não-viciado (onde cada valor tem a probabilidade $1/6$) é
```
lado <- 1:6
p <- 1/6
sum(lado * p)
```
```
## [1] 3,5
```

8.4.3 Altura de um homem adulto

Estimamos o valor esperado da população simplesmente calculando a média da amostra:
```
mean(homens$altura)
```
```
## [1] 1,730068
```
Se a variável aleatória $X$ é normalmente distribuída, com média $\mu$ e desvio-padrão $\sigma$, i.e., $X \sim \mathcal{N}(\mu, \sigma)$, então o valor esperado $E(X)$ é igual a $\mu$, que é o valor da integral

\[ \int_{-\infty}^{+\infty} x \cdot{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}} \text{d}x \]

8.5 Propriedades do valor esperado

Vamos ver como o valor esperado se comporta.
O valor esperado de uma constante é ela mesma:

\[ E(c) = c \]
Somar uma constante à variável $X$ altera $E(X)$ pelo valor da constante:

\[ E(X \pm c) = E(X) \pm c \]
Multiplicar a variável $X$ por uma constante multiplica $E(X)$ pelo valor da constante:

\[ E(c \cdot X) = c \cdot E(X) \]
O valor esperado da soma (resp. diferença) de duas variáveis aleatórias é a soma (resp. diferença) dos valores esperados:

\[ E(X \pm Y) = E(X) \pm E(Y) \]
O valor esperado de uma função $f(X)$ de uma variável aleatória $X$ é
- Caso discreto:
  
  \[ E(f(X)) = \sum_i f(x_i) \cdot P(X = x_i) \]
- Caso contínuo:
  
  \[ E(f(X)) = \int_{-\infty}^{+\infty} f(x) \cdot \text{fdp}(x) \text{d}x \]

8.6 Variância

A variância de uma variável aleatória $X$ é a média ponderada dos desvios quadrados, com as probabilidades como peso.
- Caso discreto:
  
  \[ \sigma^2(X) = \sum_i (x_i - \mu)^2 \cdot P(X = x_i) \]
- Caso contínuo:
  
  \[ \sigma^2(X) = \int_{-\infty}^{+\infty} (x - \mu)^2 \cdot \text{fdp}(x) \text{d}x \]
Em qualquer caso,

\[ \begin{aligned} \sigma^2(X) &= E[(X - \mu)^2]\\ &= E(X^2) - [E(X)]^2 \end{aligned} \]
Faça as contas, partindo de $E[(X - \mu)^2]$ e usando as propriedades do valor esperado para chegar a $E(X^2) - [E(X)]^2$.

8.6.1 Lançar dois dados

A variância é

dados_distr %>% 
  summarize(s2 = sum((x - 7)^2 * num)) %>% 
  pull(s2)

## [1] 5,833333

8.6.2 Lançar um dado

A variância é

lado <- 1:6
p <- 1/6
sum((lado - 3.5)^2 * p)

## [1] 2,916667

8.6.3 Altura de um homem adulto

Estimando pela variância da amostra:
```
var(homens$altura)
```
```
## [1] 0,00490808
```
Se $X$ é normalmente distribuída com média $\mu$ e desvio-padrão $\sigma$, i.e., $X \sim \mathcal{N}(\mu, \sigma)$, então $\sigma^2(X) = \sigma^2$. De acordo com o estudo, $\sigma^2 = 0.07^2 = 0{,}0049$.

8.7 Propriedades da variância

A variância de uma constante é zero:

\[ \sigma^2(c) = 0 \]
Somar uma constante à variável $X$ não altera a variância:

\[ \sigma^2(X \pm c) = \sigma^2(X) \]
Multiplicar a variável $X$ por uma constante multiplica a variância pelo quadrado da constante:

\[ \sigma^2(c \cdot X) = c^2 \cdot \sigma^2(X) \]
A variância da soma ou diferença de duas variáveis aleatórias é a soma das variâncias das variáveis:

\[ \sigma^2(X \pm Y) = \sigma^2(X) + \sigma^2(Y) \]
Por que a variância da diferença é a soma das variâncias?

Variância significa incerteza.

Considere o seguinte exemplo para entender por que $\sigma^2(X - Y) = \sigma^2(X) + \sigma^2(Y)$:
- Você compra uma caixa de $500$g de cereal no mercado. Como o peso não é exato, considere que $X$ é a variável aleatória que representa o peso do cereal na caixa, com $\mu_X = 500$g e uma variância qualquer $\sigma^2_X$ (que corresponde à incerteza do processo de embalagem do cereal na fábrica).
- Você decide comer $100\text{g}$ de cereal, despejando parte do conteúdo na caixa em uma tigela. Como sua capacidade de medir $100\text{g}$ não é exata, considere que $Y$ é a variável aleatória que representa o peso do cereal na tigela, com $\mu_Y = 100\text{g}$ e uma variância qualquer $\sigma^2_Y$ (que corresponde à incerteza do seu processo de pesar $100\text{g}$).
- Considere a variável aleatória $Z = X - Y$, que representa a quantidade de cereal que sobrou na caixa.
  - Certamente a média $\mu_Z = \mu_X - \mu_Y = 400\text{g}$.
  - E a variância $\sigma^2_Z$?
  - O fato de $Z$ ser o resultado da subtração de duas variáveis aleatórias diminui a incerteza?
  - Ou a composição de incertezas aumenta a incerteza?

8.8 Mais exemplos

8.8.1 Seguradora

Você tem uma seguradora, com $1.000$ segurados, cada um deles pagando $50$ dinheiros por ano.
Por ano, $1$ dos $1.000$ segurados morre. Neste caso, sua seguradora deve pagar $10.000$ dinheiros.
Por ano, $2$ dos $1.000$ segurados ficam inválidos. Neste caso, sua seguradora deve pagar $5.000$ dinheiros.
Quanto sua seguradora espera ter de lucro (ou prejuízo) por segurado, por ano?
- Chamando de $X$ a variável aleatória que representa o dinheiro pago pela seguradora por apólice, por ano, temos
  
  \[ \begin{aligned} P(X = 10000) &= 1/1000\\ P(X = 5000) &= 2/1000\\ P(X = 0) &= 997/1000 \end{aligned} \]
- Daí,
\[ \begin{aligned} E(X) &= 10000 \cdot \frac{1}{1000} \;+\; 5000 \cdot \frac{2}{1000} \;+\; 0 \cdot \frac{997}{1000} \\ &= 20 \end{aligned} \]
- Como cada segurado paga $50$ dinheiros por ano, sua seguradora lucra, em média, $30$ dinheiros por apólice, por ano.
E o desvio-padrão?
- Calculando a variância antes:
  
  \[ \begin{aligned} \sigma^2(X) &= (10000 - 20)^2 \cdot \frac{1}{1000} \;+\; (5000 -20)^2 \cdot \frac{2}{1000} \;+\; (0 - 20)^2 \cdot \frac{997}{1000} \\ &= 9980^2 \cdot \frac{1}{1000} \;+\; 4980^2 \cdot \frac{2}{1000} \;+\; (- 20)^2 \cdot \frac{997}{1000} \\ &= 149600 \end{aligned} \]
- O desvio-padrão é a raiz quadrada de $\sigma^2$:
  
  \[ \sigma = 386{,}78 \]

8.8.2 Gerador de números aleatórios

Você programa um gerador de números aleatórios $x \in [1, 3] \subset \mathbb{R}$.
Considere $X$ a variável aleatória que representa os números gerados.
$X$ é uma variável aleatória contínua, com fdp

\[ f(x) = \begin{cases}\displaystyle \frac{1}{2} & \text{se } x \in [1, 3] \\ \,0 & \text{se } x \not\in [1, 3] \end{cases} \]

cujo gráfico é
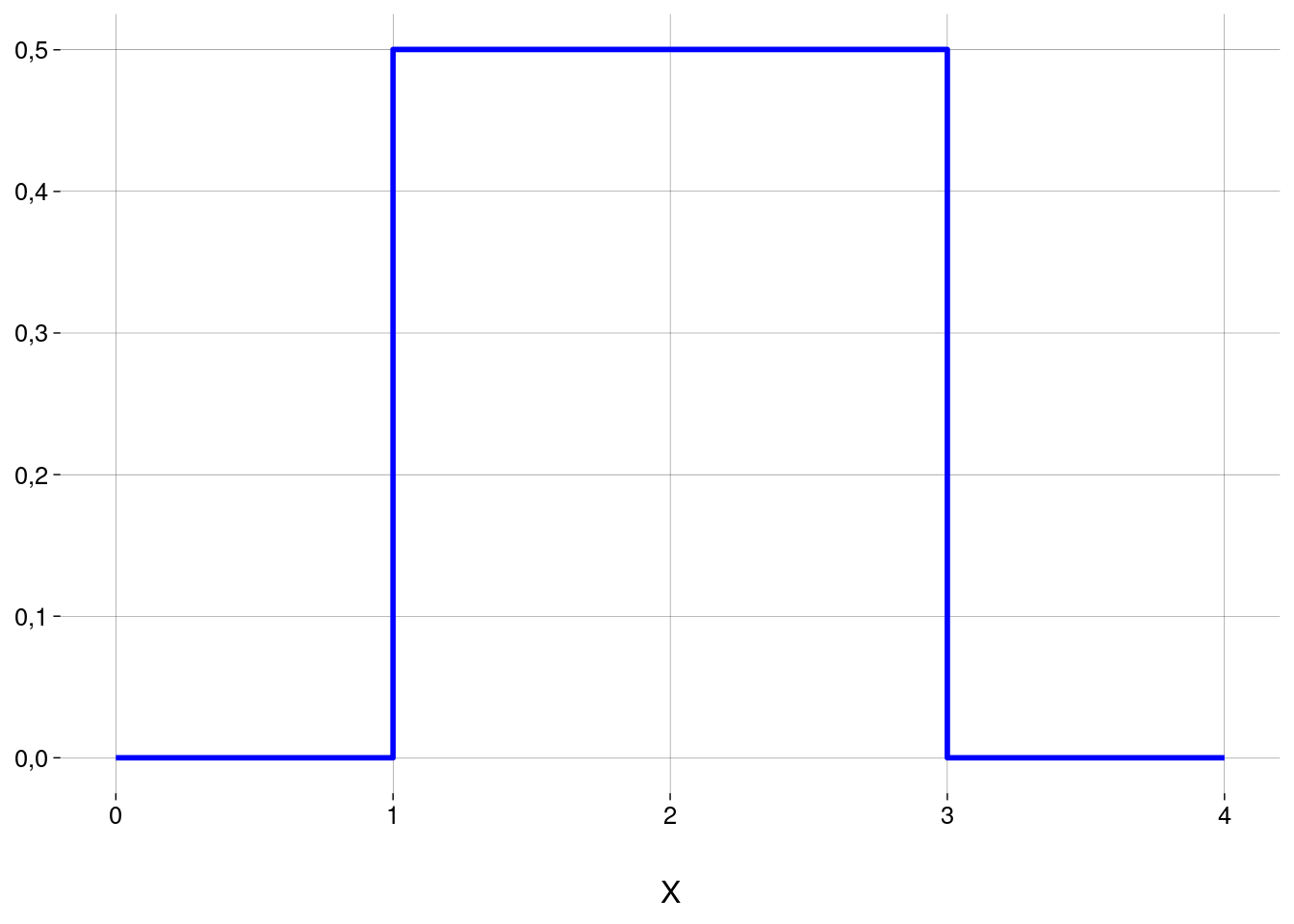
Isto significa que a densidade de probabilidade está distribuída uniformemente no intervalo $[1, 3]$.
Vamos calcular o valor esperado $E(X)$:

\[ \begin{aligned} E(X) &= \int_{-\infty}^{+ \infty} x \cdot f(x) \text{d}x \\ &= \int_{1}^{3} x \cdot \frac{1}{2} \text{d}x \\ &= \frac12 \cdot \left.\frac{x^2}{2} \right|_1^3 \\ &= 2 \end{aligned} \]
Ou seja, a média dos números gerados, depois de muitas execuções, vai ser $2$.
Vamos calcular a variância $\sigma^2(X)$:

\[ \begin{aligned} \sigma^2(X) &= \int_{-\infty}^{+ \infty} (x - 2)^2 \cdot f(x) \text{d}x \\ &= \int_{1}^{3} (x-2)^2 \cdot \frac{1}{2} \text{d}x \\ &= \frac13 \end{aligned} \]

Isto vai dar um desvio-padrão $\sigma = \sqrt{\sigma^2} = \frac{\sqrt{3}}{3} \approx 0{,}58$.

Mas R tem este gerador! Vamos gerar muitos valores e calcular a média e o desvio-padrão:

valores <- runif(n = 1e6, min = 1, max = 3)
mean(valores)

## [1] 1,999971

sd(valores)

## [1] 0,5772607

Como exercício, verifique que, para qualquer variável aleatória contínua $X$ distribuída uniformemente entre $a$ e $b$, i.e., com fdp

\[ f(x) = \begin{cases}\displaystyle \frac{1}{b - a} & \text{se } x \in [a, b] \\ \,0 & \text{se } x \not\in [a, b] \end{cases} \]

ocorre que
- $E(X) = \frac{a+b}{2}$, e
- $\sigma^2(X) = \frac{(a - b)^2}{12}$.

7 Probabilidades

9 Distribuições discretas