Capítulo 10 Distribuições contínuas

10.1 Vídeo

10.2 Distribuição uniforme

10.2.1 Exemplo: gerador de números aleatórios

• Um programa para gerar números reais aleatórios no intervalo \([0, 10]\).

• A probabilidade é distribuída uniformemente neste intervalo.

• A variável aleatória \(X\) representa os números gerados.

\(P(X = x) = 0!\)

Como \(X\) é uma variável aleatória contínua, as probabilidades \(P(X = 1)\), \(P(X = 3{,}1416)\), ou qualquer outra probabilidade pontual \(P(X = x)\), são iguais a zero!

• A fdp (função de densidade de probabilidade) de \(X\) é

  \[ f(x) = \begin{cases} \frac{1}{10} & \text{se } x \in [0, 10] \\ 0 & \text{se } x \not\in [0, 10] \end{cases} \]

  cujo gráfico é

  

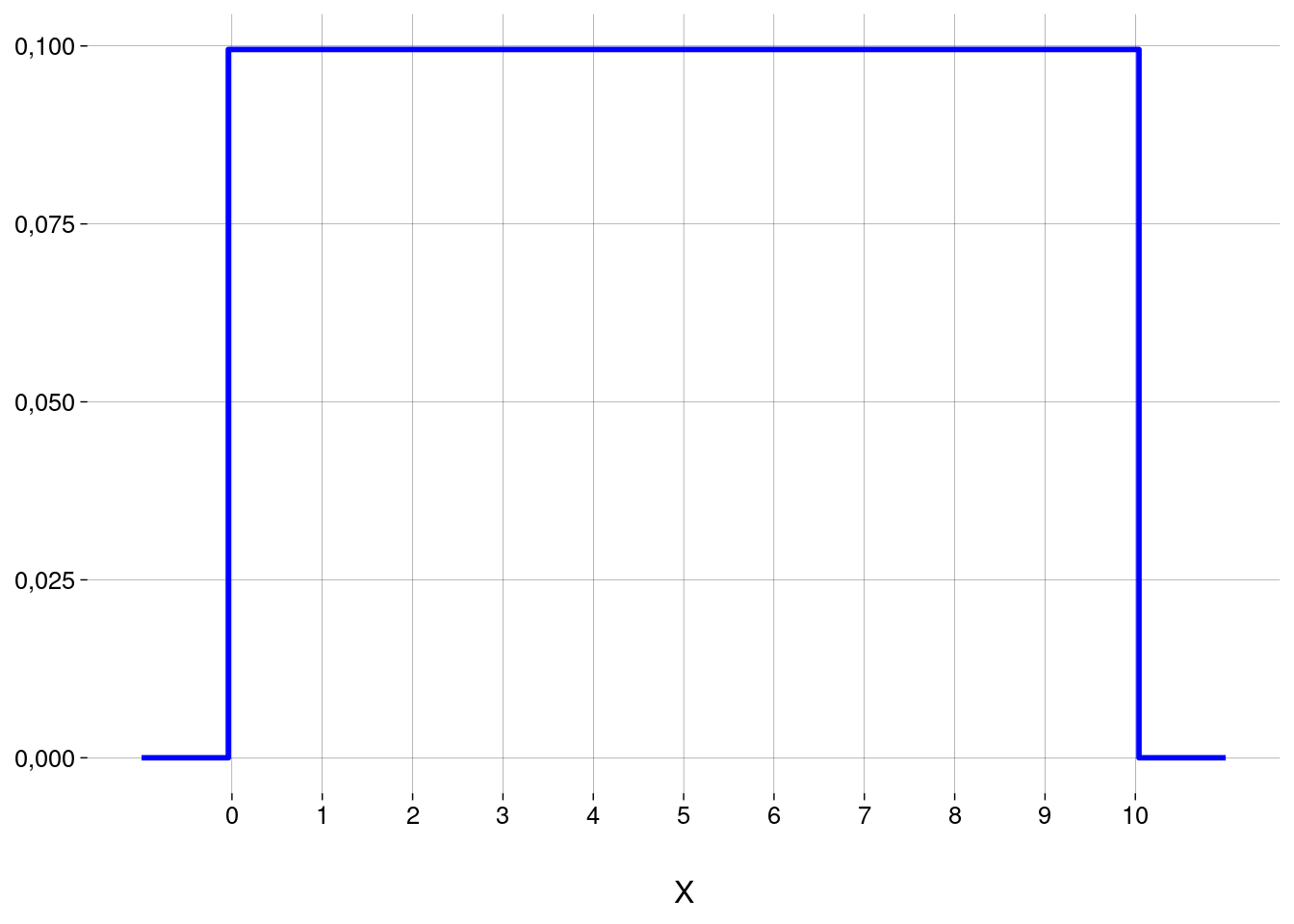
Densidade não é probabilidade!

Perceba que a probabilidade \(P(X = 5)\) é \(0\), mas a densidade \(f(5)\) é \(1/10\).

• A probabilidade de um número gerado estar entre \(5\) e \(7\) é de

  \[ P(5 < X < 7) = P(5 \leq X \leq 7) = \int_5^7 f(x)\;\text{d}x = \int_5^7 \frac{1}{10}\;\text{d}x = \frac{1}{5} \]

• O valor esperado de \(X\) é

  \[ E(X) = \int_{-\infty}^{\infty} xf(x)\;\text{d}x = \int_{0}^{10} \frac{1}{10}x\;\text{d}x = 5 \]

• A variância de \(X\) é

  \[ \sigma^2(X) = \int_{-\infty}^{+ \infty} (x - 5)^2 \cdot f(x)\;\text{d}x = \int_{0}^{10} (x-5)^2 \cdot \frac{1}{10}\;\text{d}x = \frac{25}{3} = 8{,}33 \]

• Exercício: calcule \(\sigma^2(X)\) usando a fórmula \(\sigma^2(X) = E(X^2) - [E(X)]^2\).

10.2.2 No geral

• Escrevemos \(X \sim \text{Unif} (a, b)\).

• Os extremos do intervalo são \(a, b \in \mathbb{R}, a < b\).

• O suporte é o intervalo \([a, b]\).

• A função de densidade de probabilidade é

  \[ f(x \mid a, b) = \begin{cases} \frac{1}{b - a} & \text{se } x \in [a, b] \\ 0 & \text{se } x \not\in [a, b] \end{cases} \]

• Valor esperado:

  \[E(X) = \frac{a+b}{2}\]

• Variância:

  \[\sigma^2(X) = \frac{(a - b)^2}{12}\]

10.2.3 Em R

Função de densidade de probabilidade: \(f(x \mid a, b)\)

• dunif(x, min = a, max = b).

• No exemplo do gerador de números aleatórios em \([0, 10]\), todos os valores no intervalo têm a mesma densidade: \(\frac{1}{10}\). Valores fora do intervalo têm densidade \(0\):

  dunif(
    c(-1, 1, 2, 10, 11), 
    min = 0,
    max = 10
  )

  ## [1] 0,0 0,1 0,1 0,1 0,0

Função de probabilidade acumulada: \(\text{Unif}(X \leq q \mid a, b)\)

• punif(q, min = a, max = b).

• No exemplo do gerador de números aleatórios no intervalo \([0, 10]\), qual a probabilidade de obter um número menor que \(4\)?

  punif(4, min = 0, max = 10)

  ## [1] 0,4

• E um número maior que \(4\)?

  punif(4, min = 0, max = 10, lower.tail = FALSE)

  ## [1] 0,6

Função quantil: dado um valor de \(\text{Unif}(X \leq x \mid a, b)\), então \(x = ?\)

• O objetivo é achar \(x\) tal que \(\text{Unif}(X \leq x \mid a, b) = m\).

• qunif(p, min = a, max = b).

• No exemplo do gerador de números aleatórios no intervalo \([0, 10]\), qual o número \(x\) tal que existe uma probabilidade de \(80\%\) de que um número menor ou igual a \(x\) seja gerado?

  qunif(.8, min = 0, max = 10)

  ## [1] 8

• E qual o número \(x\) tal que existe uma probabilidade de \(80\%\) de que um número maior ou igual a \(x\) seja gerado?

  qunif(.8, min = 0, max = 10, lower.tail = FALSE)

  ## [1] 2

Função para gerar números aleatórios

• runif(n, min = a, max = b)

• Os números gerados são de ponto flutuante:

  runif(10, min = 0, max = 10)

  ##  [1] 8,0446404 2,7052190 8,7356228 6,3046186 4,6212423 6,1559463 3,1436863 3,0824766
  ##  [9] 4,0517886 0,6781619

• Exercício: e se você quiser gerar apenas números inteiros no intervalo dado?

• Exercício: os extremos do intervalo (min e max) podem ser gerados?

10.3 Distribuição normal

10.3.1 Exemplo

• Segundo o Levantamento do Perfil Antropométrico da População Brasileira Usuária do Transporte Aéreo Nacional, em 2009, a estatura do homem brasileiro adulto era distribuída normalmente, com média \(1{,}73\)m e desvio-padrão \(0{,}07\)m.

• Segundo este livro, a estatura do homem holandês é distribuída normalmente, com média \(1{,}84\)m e desvio-padrão \(0{,}08\)m.

  mu_brasil <- 1.73
  sigma_brasil <- .07
  
  mu_holanda <- 1.84
  sigma_holanda <- .08

• Gráfico:

  

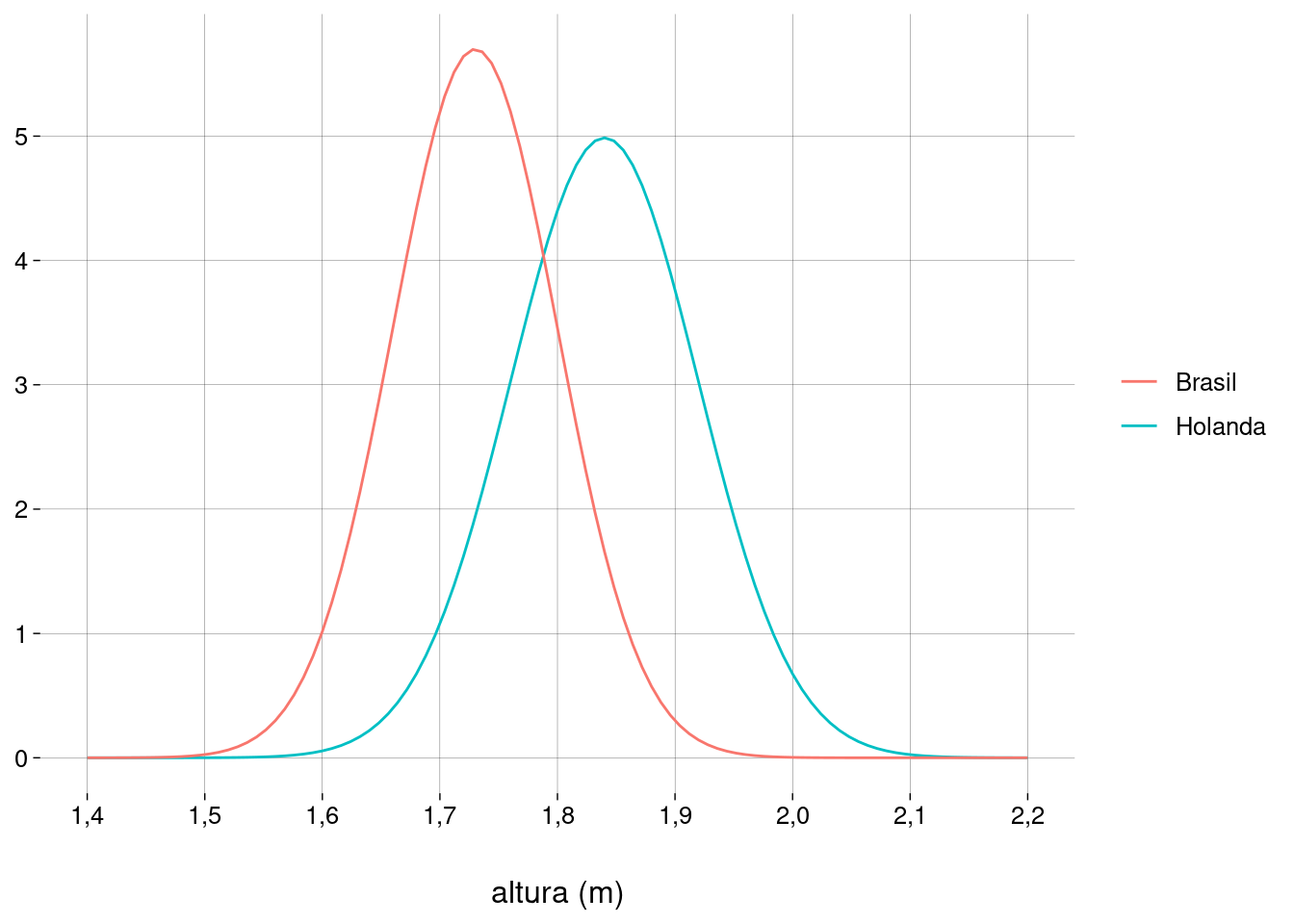
• Exercício: o que são os números no eixo vertical?

• Por que a curva do Brasil é mais alta?

10.3.2 No geral

• Escrevemos \(X \sim \mathcal{N}(\mu, \sigma)\).

• O valor esperado é \(\mu \in \mathbb{R}\).

• O desvio-padrão é \(\sigma \in \mathbb{R}_{\geq 0}\).

• O suporte é o intervalo\((-\infty, \infty)\).

• A função de densidade de probabilidade é:

  \[ f(x \mid \mu, \sigma) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x - \mu}{\sigma}\right)^2} \]

10.3.3 Em R

Função de densidade de probabilidade: \(f(x \mid \mu, \sigma)\)

• dnorm(x, mean = μ, sd = σ).

Função de probabilidade acumulada: \(\text{Norm}(X \leq q \mid \mu, \sigma)\)

• pnorm(q, mean = μ, sd = σ).

• Qual a probabilidade de um homem brasileiro ter entre \(1{,}80\)m e \(1{,}90\)m de altura?

• Gráfico:

  

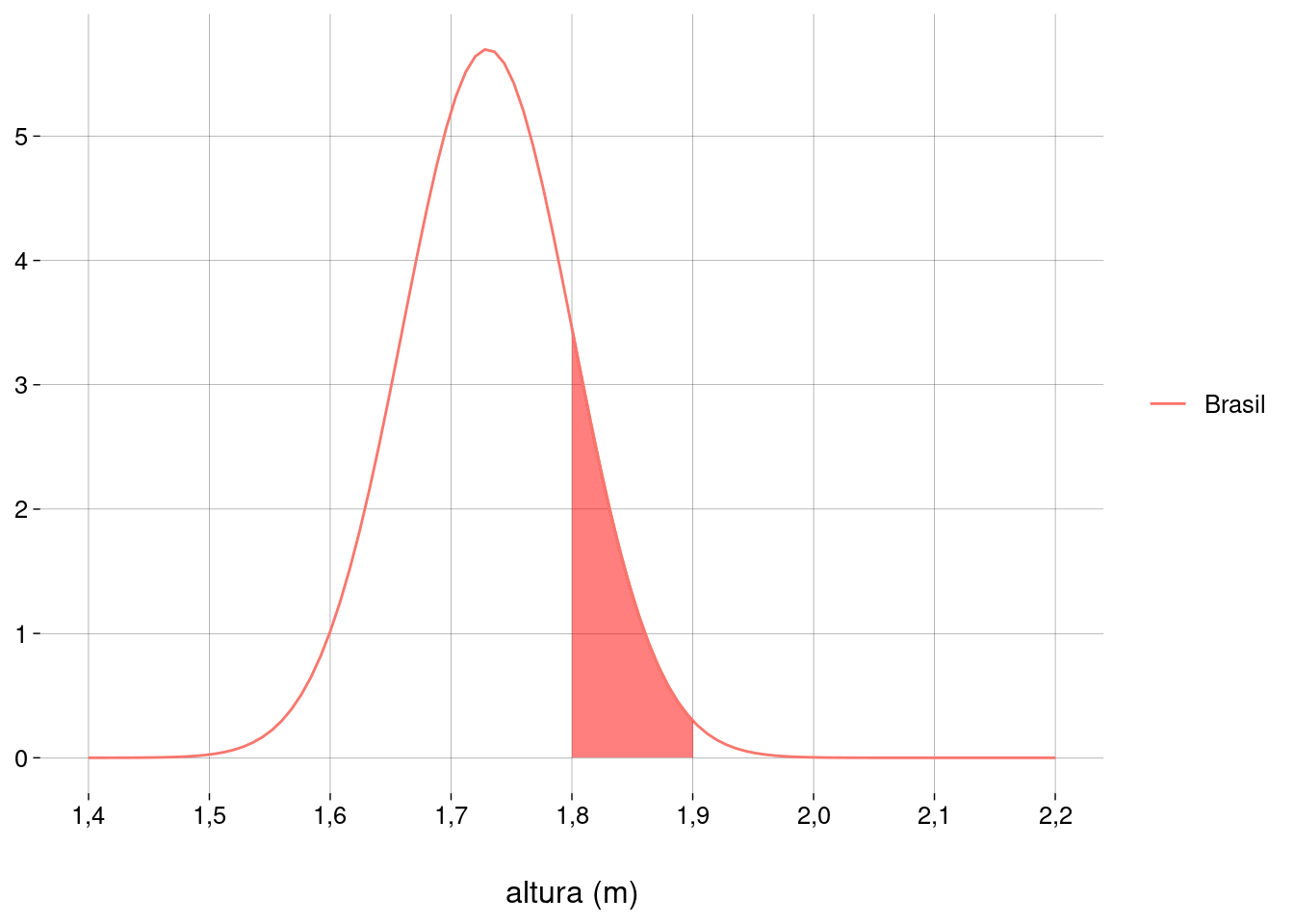
• Menos que \(1{,}80\)m:

  pnorm(1.80, mu_brasil, sigma_brasil)

  ## [1] 0,8413447

• Menos que \(1{,}90\)m:

  pnorm(1.90, mu_brasil, sigma_brasil)

  ## [1] 0,9924208

• Entre \(1{,}80\)m e \(1{,}90\)m:

  pnorm(1.90, mu_brasil, sigma_brasil) - 
    pnorm(1.80, mu_brasil, sigma_brasil)

  ## [1] 0,151076

• Qual a probabilidade de um homem holandês ter entre \(1{,}80\)m e \(1{,}90\)m de altura?

• Gráfico:

  

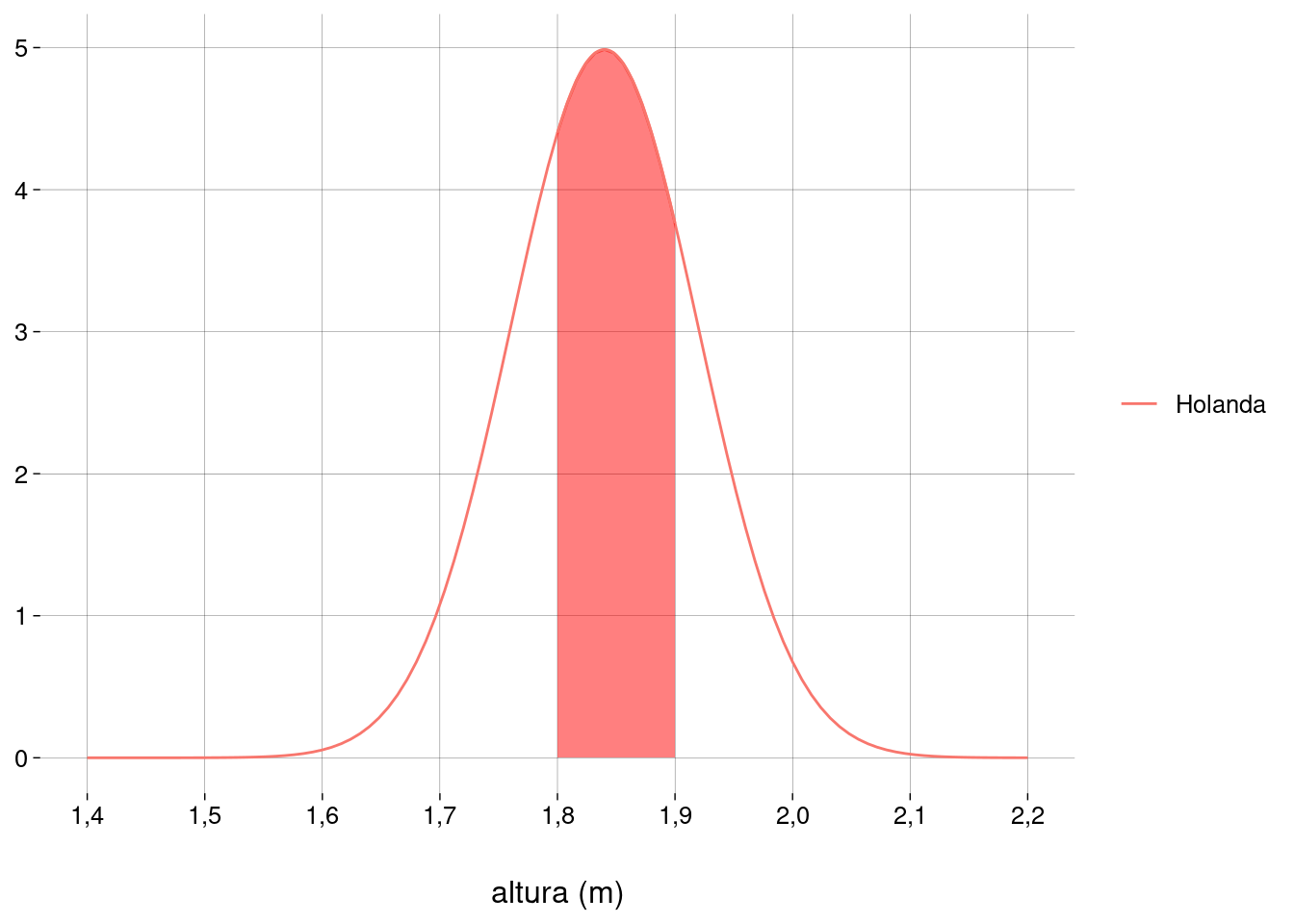
• Menos que \(1{,}80\)m:

  pnorm(1.80, mu_holanda, sigma_holanda)

  ## [1] 0,3085375

• Menos que \(1{,}90\)m:

  pnorm(1.90, mu_holanda, sigma_holanda)

  ## [1] 0,7733726

• Entre \(1{,}80\)m e \(1{,}90\)m:

  pnorm(1.90, mu_holanda, sigma_holanda) - 
    pnorm(1.80, mu_holanda, sigma_holanda)

  ## [1] 0,4648351

Função quantil: dado um valor de \(\text{Norm}(X \leq x \mid \mu, \sigma)\), então \(x = ?\)

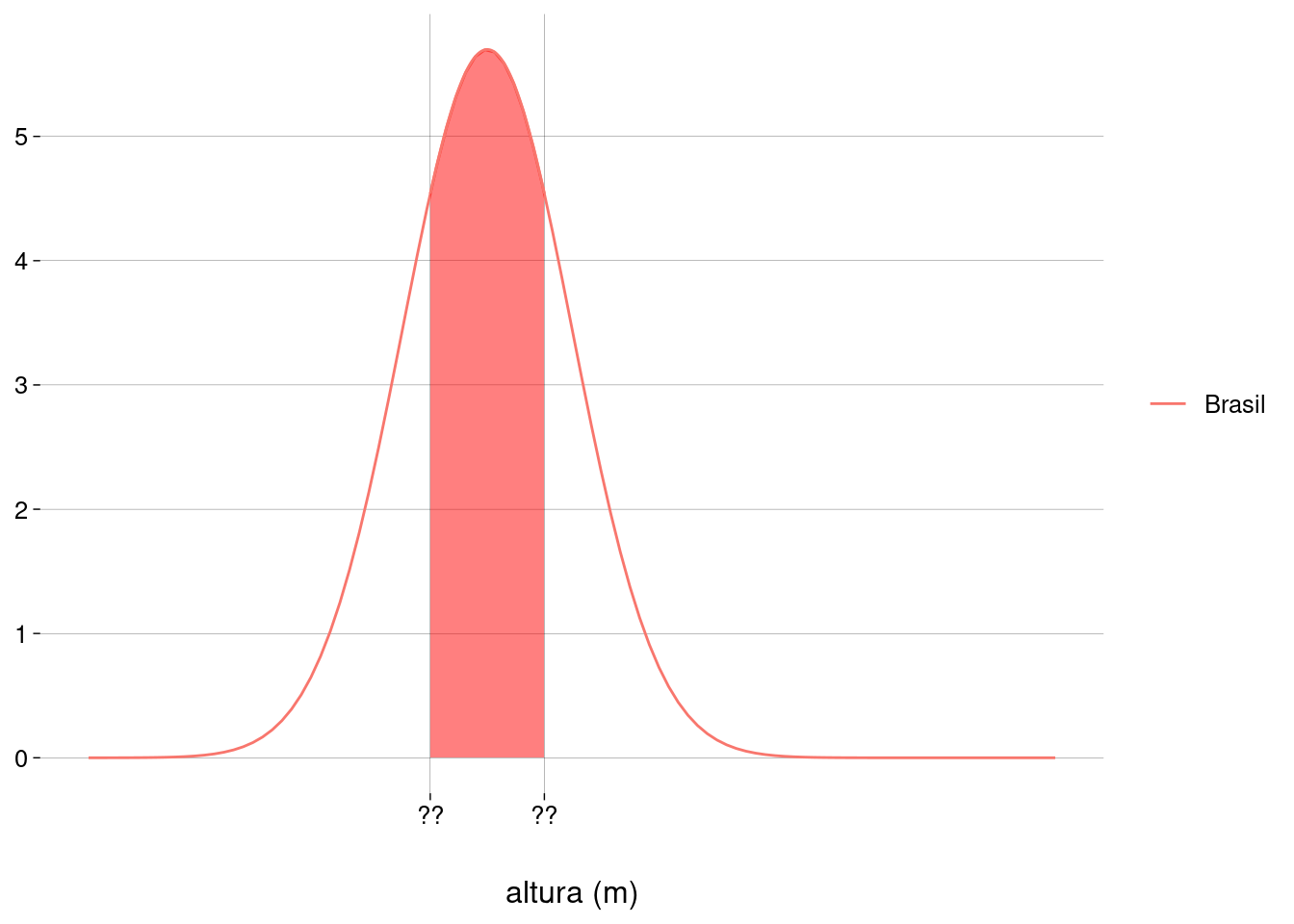
• qnorm(p, mean = μ, sd = σ).

• Quais as alturas mínima e máxima dos homens que estão nos \(50\%\) da população em torno da média?

• Gráfico:

  

• O limite inferior é o valor à esquerda do qual existem \(25\%\) de probabilidade:

  qnorm(.25, mu_brasil, sigma_brasil)

  ## [1] 1,682786

• O limite superior é o valor à esquerda do qual existem \(75\%\) de probabilidade:

  qnorm(.75, mu_brasil, sigma_brasil)

  ## [1] 1,777214

• Ou, equivalentemente, o valor à direita do qual existem \(25\%\) de probabilidade:

  qnorm(.25, mu_brasil, sigma_brasil, lower.tail = FALSE)

  ## [1] 1,777214

• As alturas mínima e máxima dos homens que estão nos \(50\%\) da população em torno da média são \(1{,}68\)m e \(1{,}78\)m.

Função para gerar números aleatórios

• rnorm(n, mean = μ, sd = σ).

• Qual é a probabilidade de um homem holandês escolhido ao acaso ser mais baixo do que um homem brasileiro escolhido ao acaso?

• Vamos responder fazendo uma simulação.

• Vamos repetir muitas vezes o experimento de escolher um holandês ao acaso e um brasileiro ao acaso:

  n <- 1e6
  holandeses <- rnorm(n, mu_holanda, sigma_holanda)
  brasileiros <- rnorm(n, mu_brasil, sigma_brasil)

• Qual a proporção de vezes em que o holandês é mais baixo?

  mean(holandeses < brasileiros)

  ## [1] 0,150629

• Segundo nossa simulação, esta é a resposta.

10.3.4 QQplots

• Como saber se um conjunto de dados numéricos segue a distribuição normal?

• Vamos gerar dados aproximadamente normais (média \(0\), desvio-padrão \(1\)):

valores <- rnorm(1000)
head(valores)

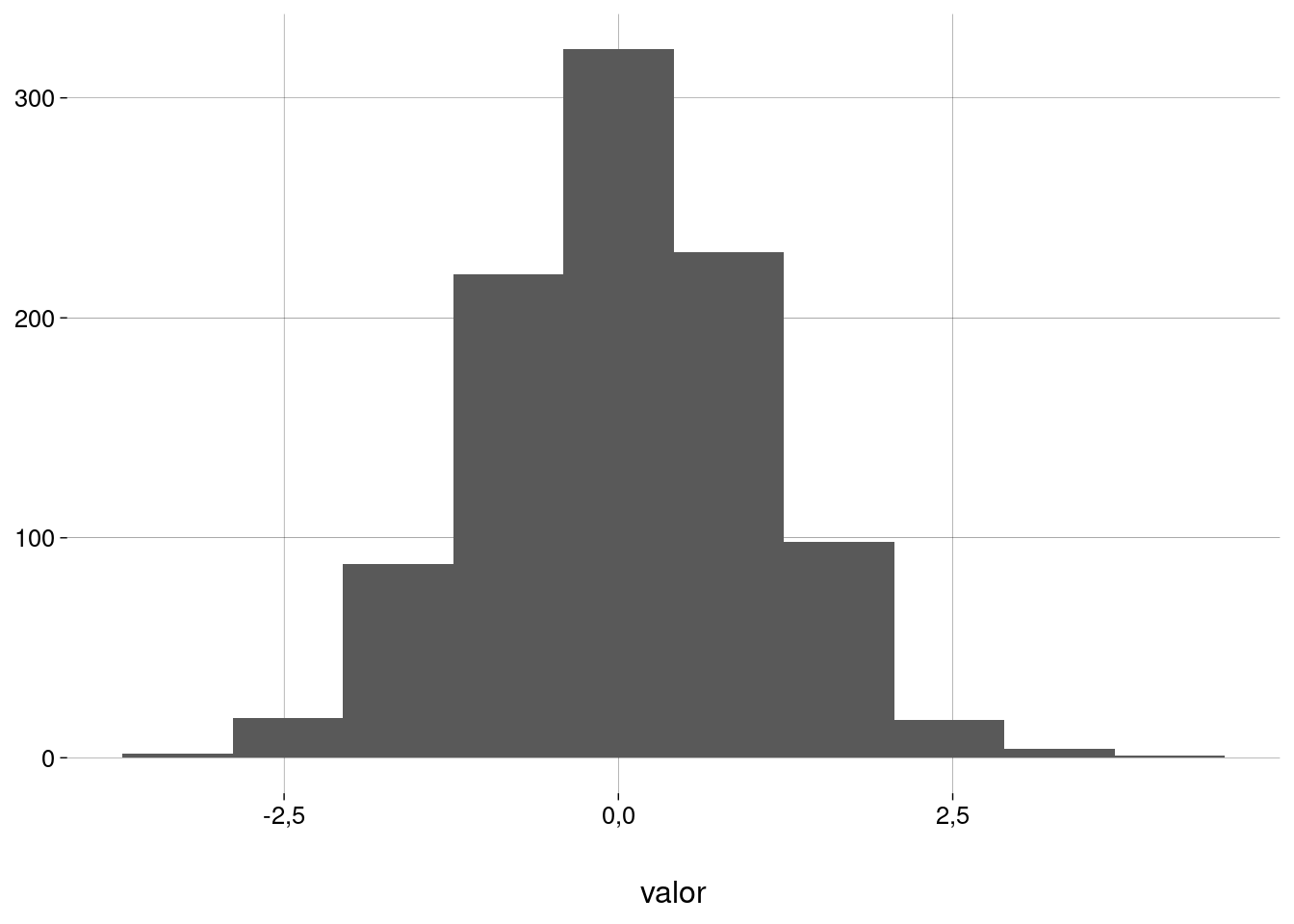
## [1]  1,1990763 -2,2858432 -0,4370087 -0,5767288 -0,8333627  1,0278603

• Histograma:

valores %>% 
  as_tibble() %>% 
  ggplot() +
    geom_histogram(aes(x = value), bins = 10) +
    labs(
      x = 'valor',
      y = NULL
    )

• Para estes dados, os quartis são

quantile(valores)

##          0%         25%         50%         75%        100% 
## -3,48205150 -0,61771144  0,01948869  0,73147328  3,93829553

• Na distribuição \(\mathcal{N}(0, 1)\) teórica, os quartis seriam

qnorm(c(0, .25, .5, .75, 1))

## [1]       -Inf -0,6744898  0,0000000  0,6744898        Inf

• O gráfico QQ (quantil-quantil) mostra os quantis da amostra no eixo \(y\) e os quantis teóricos no eixo \(x\). A reta vermelha serve para referência; se as duas distribuições fossem idênticas, todos os pontos estariam sobre a reta.

valores %>% 
  as_tibble() %>% 
  ggplot(aes(sample = value)) +
    geom_qq(alpha = .3) +
    labs(
      y = 'amostra',
      x = 'N(0, 1)'
    ) +
    geom_abline(color = 'red')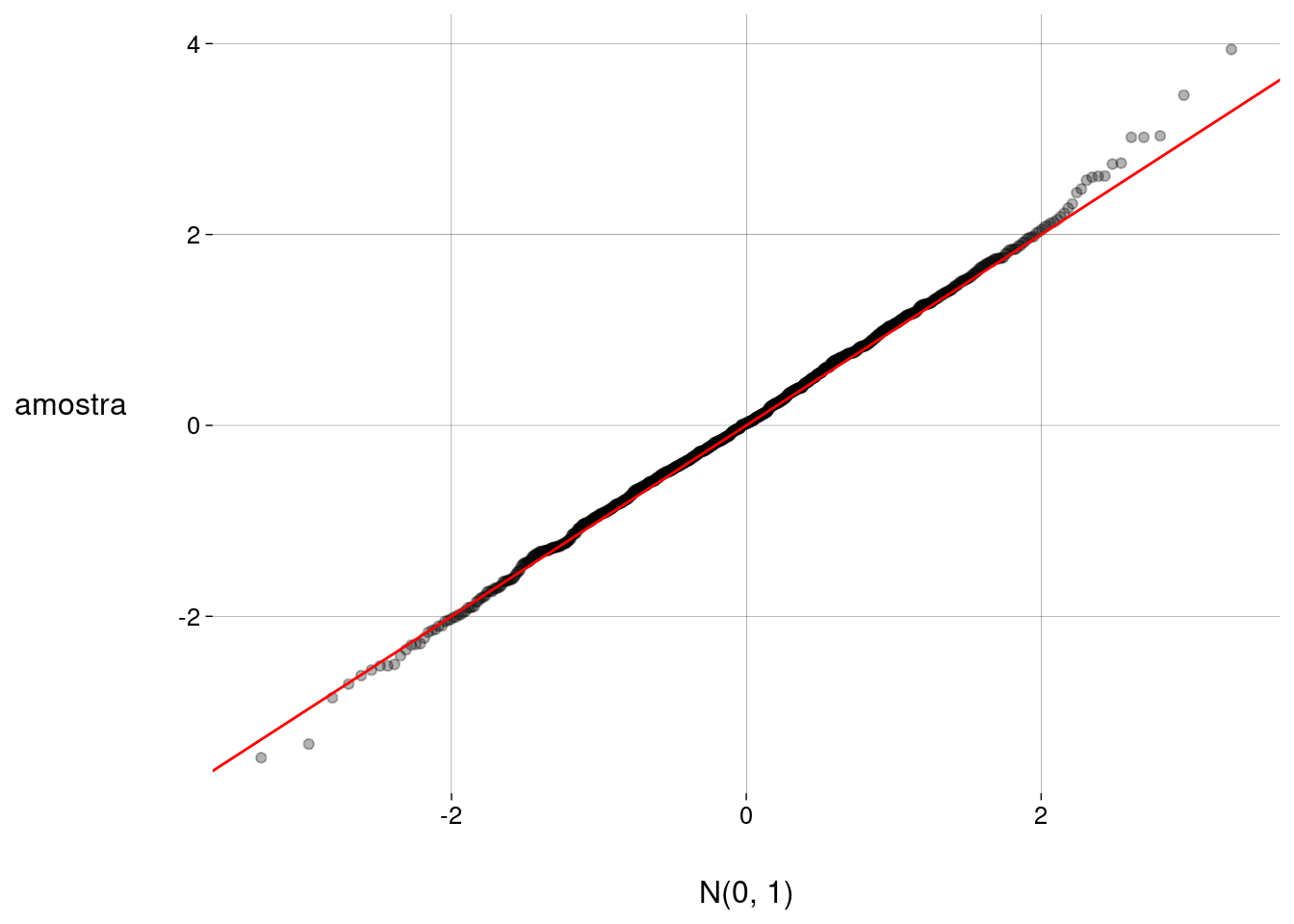

• Um exemplo concreto: pesos de \(15\) mulheres com idades entre \(30\) e \(39\) anos:

pesos <- women %>% 
  select(weight) %>% 
  transmute(peso = weight * .4535924)

• Histograma:

pesos %>% 
  ggplot() +
    geom_histogram(aes(x = peso), bins = 6) +
    labs(y = NULL)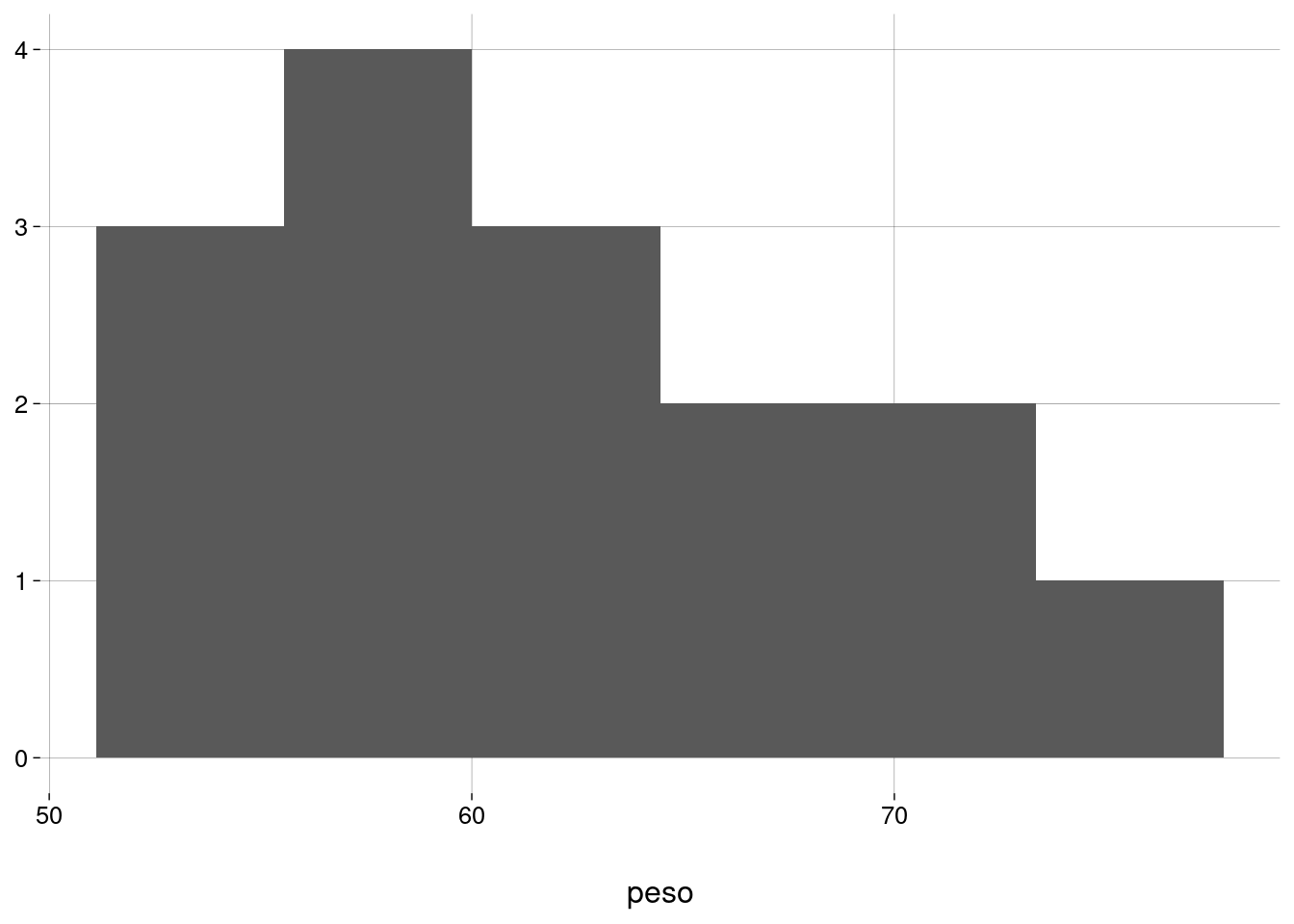

• O gráfico quantil-quantil fica

pesos %>% 
  ggplot(aes(sample = peso)) +
    geom_qq() +
    labs(
      y = 'pesos',
      x = 'N(0, 1)'
    )

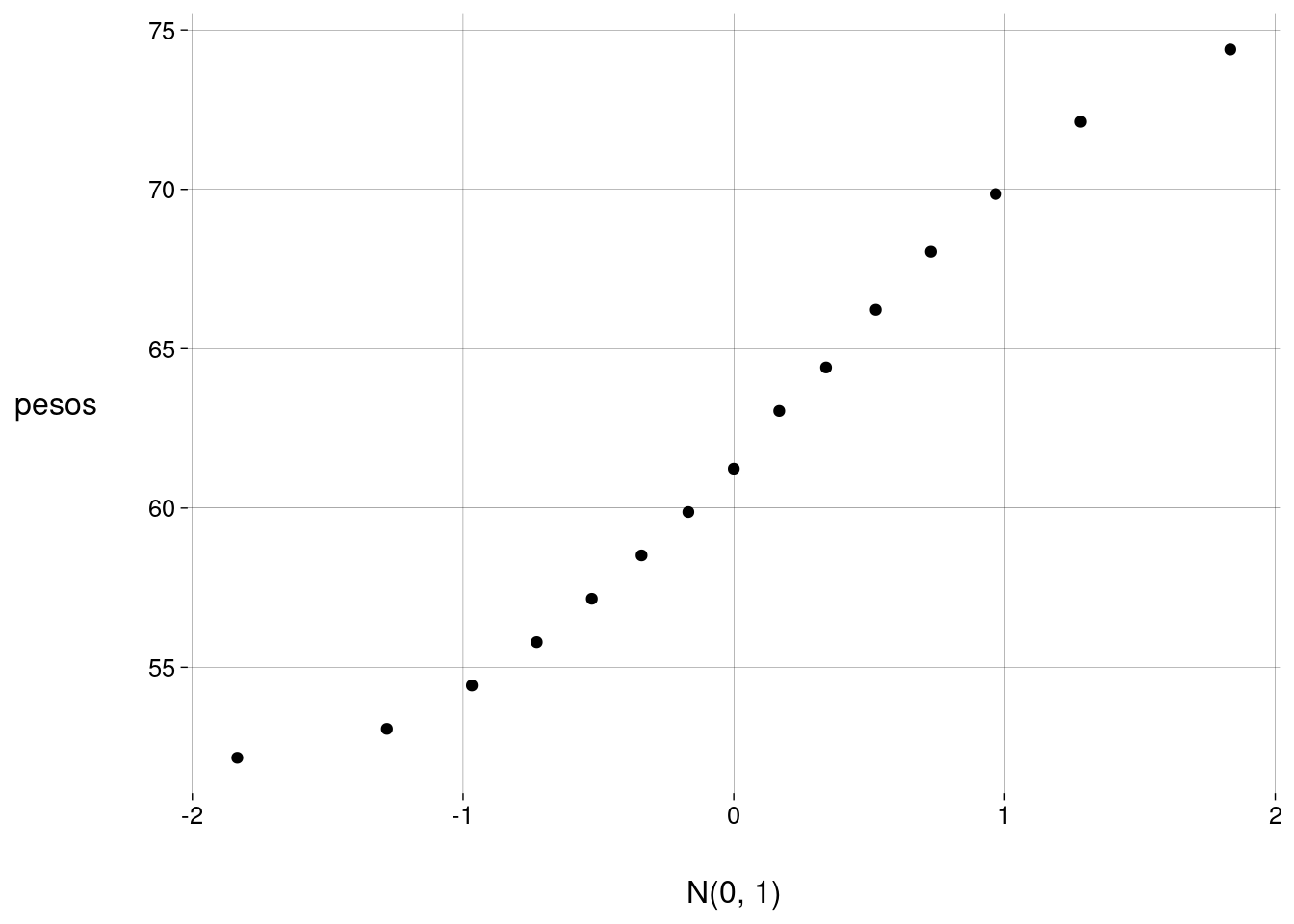
• Quanto mais próximos de uma reta com inclinação de \(45\) graus os pontos ficarem, mais próximos da distribuição normal os dados estão.

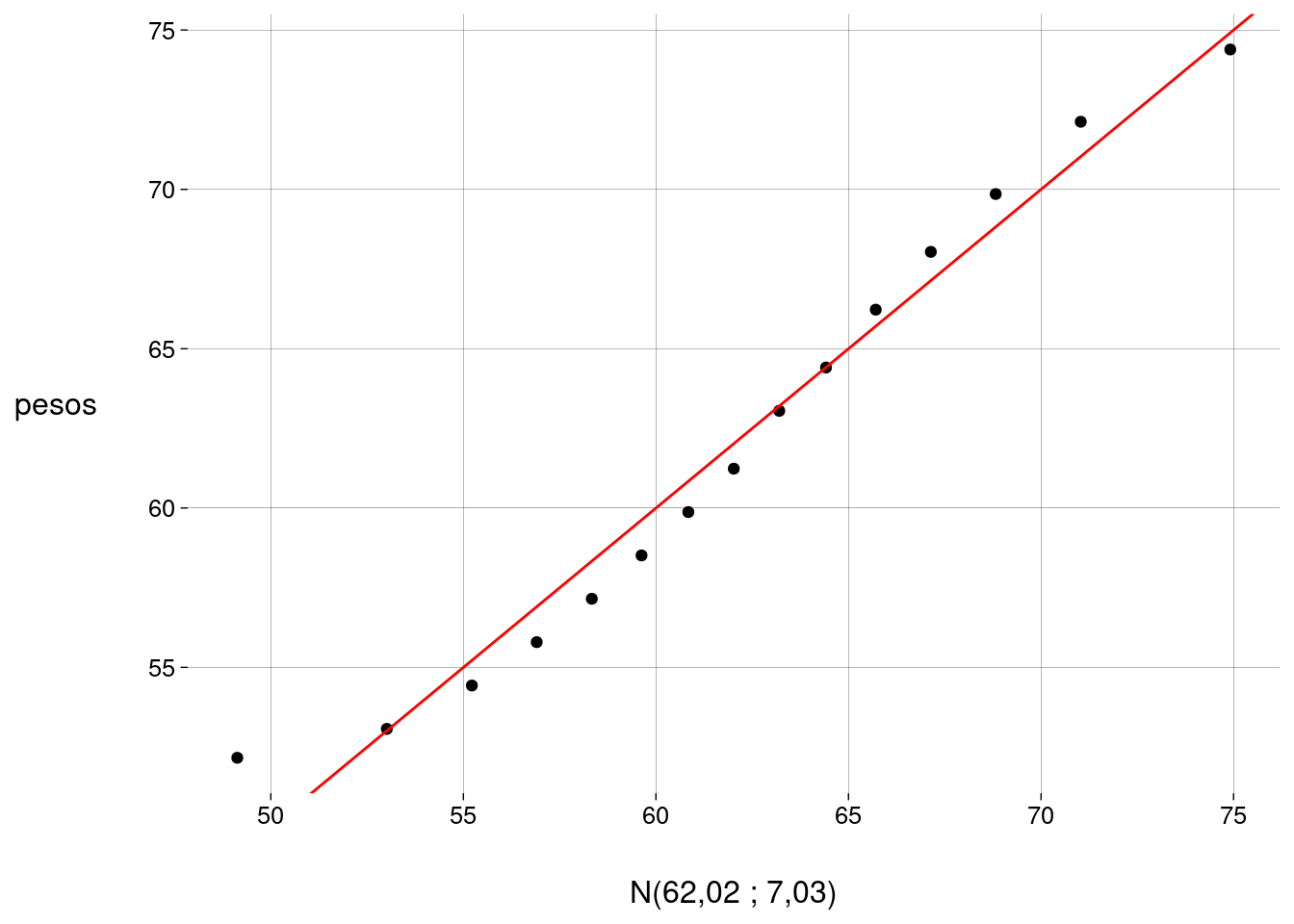
• Podemos usar, como distribuição teórica no eixo \(x\), a distribuição normal com média e desvio-padrão iguais à média e ao desvio-padrão dos dados:

m <- mean(pesos$peso)
s <- sd(pesos$peso)

pesos %>% 
  ggplot(aes(sample = peso)) +
    geom_qq(
      dparams = list(
        mean = m,
        sd = s
      )
    ) +
    geom_abline(color = 'red') +
    labs(
      y = 'pesos',
      x = paste0('N(', m %>% round(2), ' ; ', s %>% round(2), ')')
    )

• Ou podemos padronizar os dados no eixo \(y\), fazendo com que a média deles seja \(0\) e o desvio-padrão deles seja \(1\).

• Para fazer isso manualmente, basta subtrair a média e dividir pelo desvio-padrão:

pesos %>% 
  mutate(peso = (peso - mean(peso)) / sd(peso)) %>% 
  kbl(
    format.args = list(big.mark = '.')
  ) %>% 
  kable_paper(
    c('striped', 'hover'),
    full_width = FALSE
  )

peso
-1,4022687
-1,2732255
-1,0796608
-0,8860962
-0,6925315
-0,4989668
-0,3054021
-0,1118374
0,1462489
0,3398136
0,5978998
0,8559861
1,1140723
1,4366802
1,7592880

• Ou podemos usar a função scale, que faz o mesmo:

pesos %>% 
  mutate(peso = scale(peso)) %>% 
  kbl(
    format.args = list(big.mark = '.')
  ) %>% 
  kable_paper(
    c('striped', 'hover'),
    full_width = FALSE
  )

peso
-1,4022687
-1,2732255
-1,0796608
-0,8860962
-0,6925315
-0,4989668
-0,3054021
-0,1118374
0,1462489
0,3398136
0,5978998
0,8559861
1,1140723
1,4366802
1,7592880

pesos %>% 
  mutate(peso = scale(peso)) %>% 
  ggplot(aes(sample = peso)) +
    geom_qq() +
    labs(
      y = 'pesos\n(padronizados)',
      x = 'N(0, 1)'
    ) +
    geom_abline(color = 'red')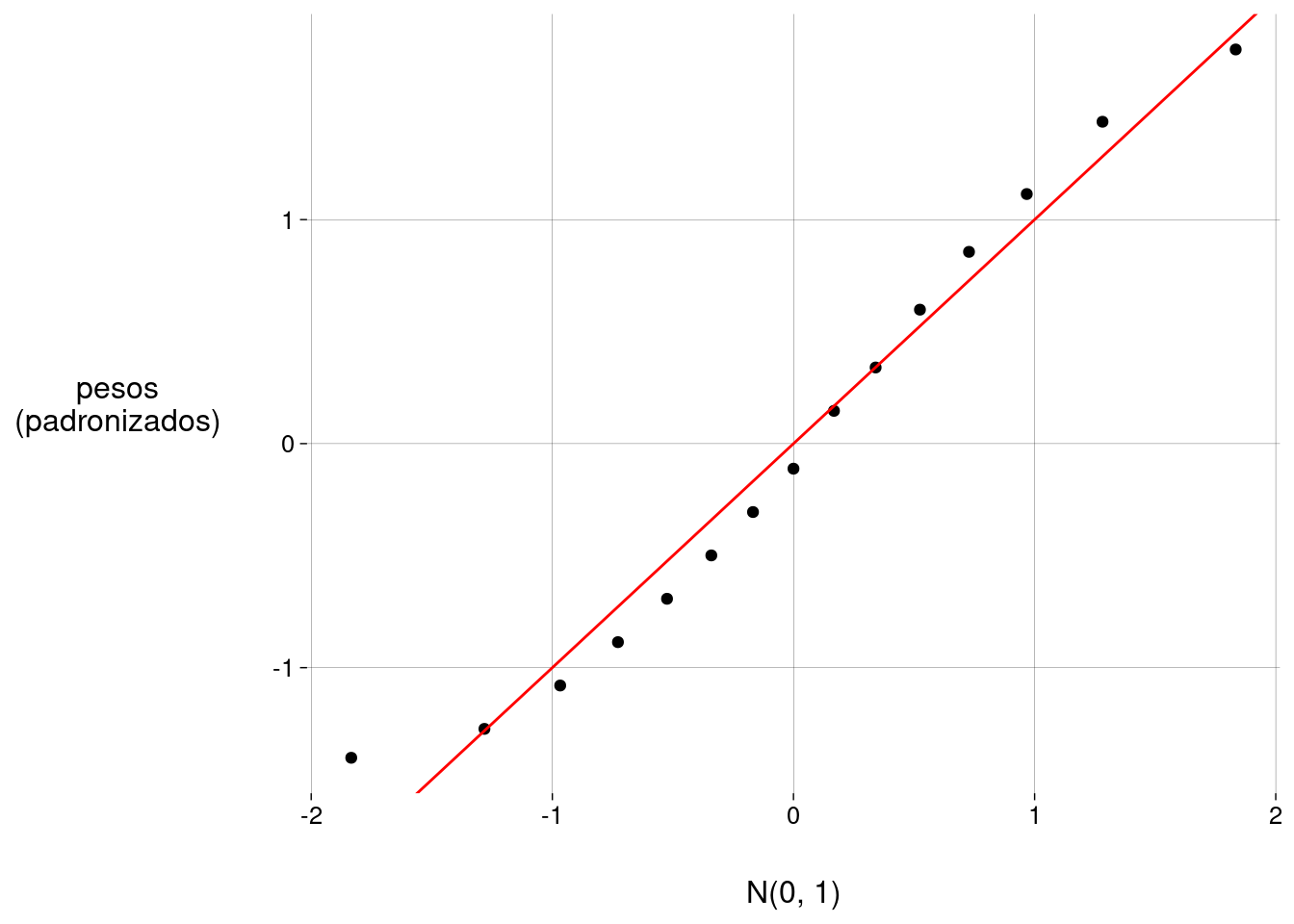

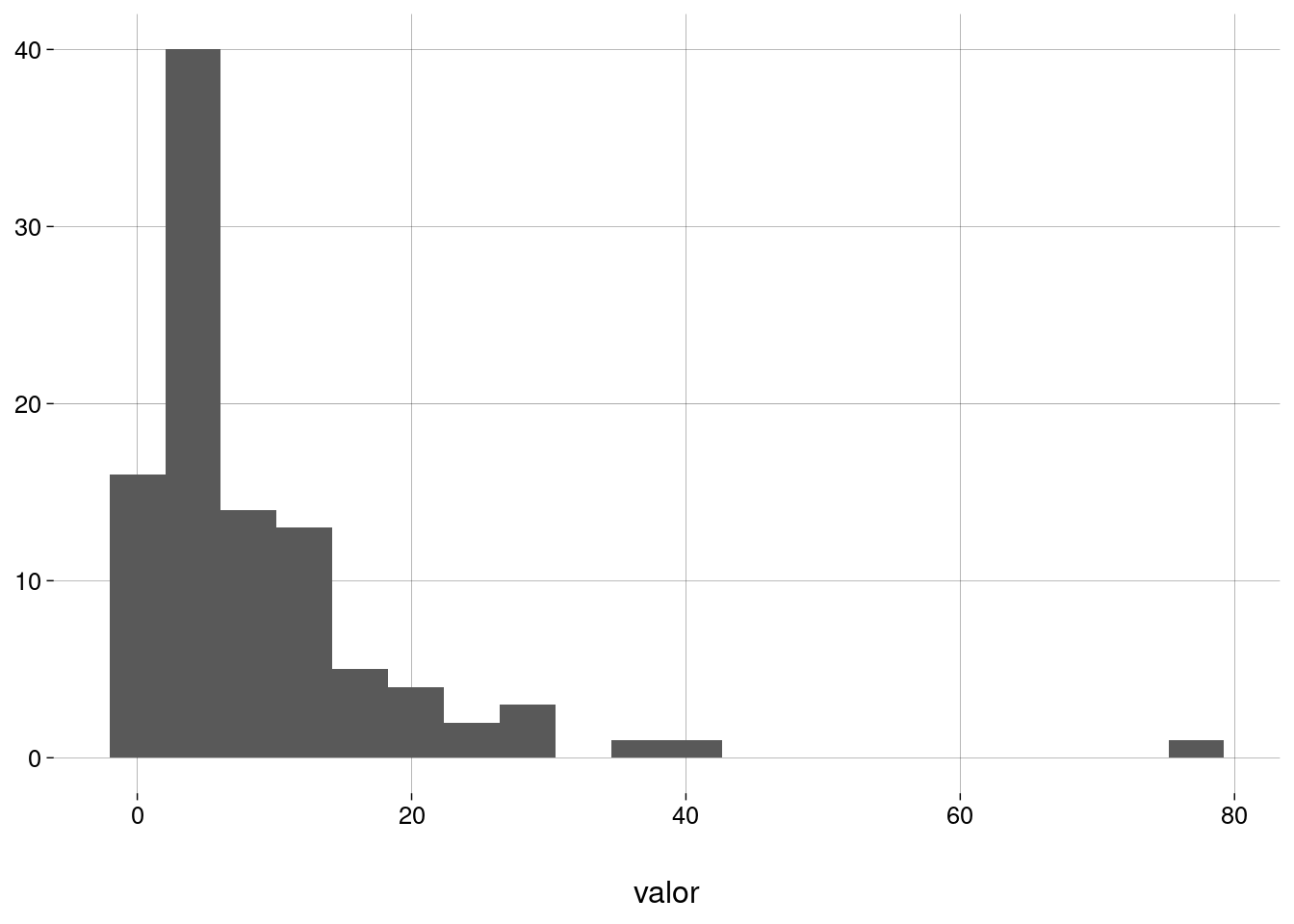
• Um exemplo de dados não normais:

dados <- rexp(100, rate = .1)
m <- mean(dados)
s <- sd(dados)

• Histograma:

dados %>% 
  as_tibble() %>% 
  ggplot() +
    geom_histogram(aes(x = value), bins = 20) +
    labs(
      x = 'valor',
      y = NULL
    )

• QQ:

dados %>% 
  as_tibble() %>% 
  ggplot(aes(sample = value)) +
    geom_qq(
      dparams = list(
        mean = m,
        sd = s
      )
    ) +
    geom_abline(color = 'red') +
    labs(
      y = 'dados',
      x = paste0('N(', m %>% round(2), ' ; ', s %>% round(2), ')')
    )

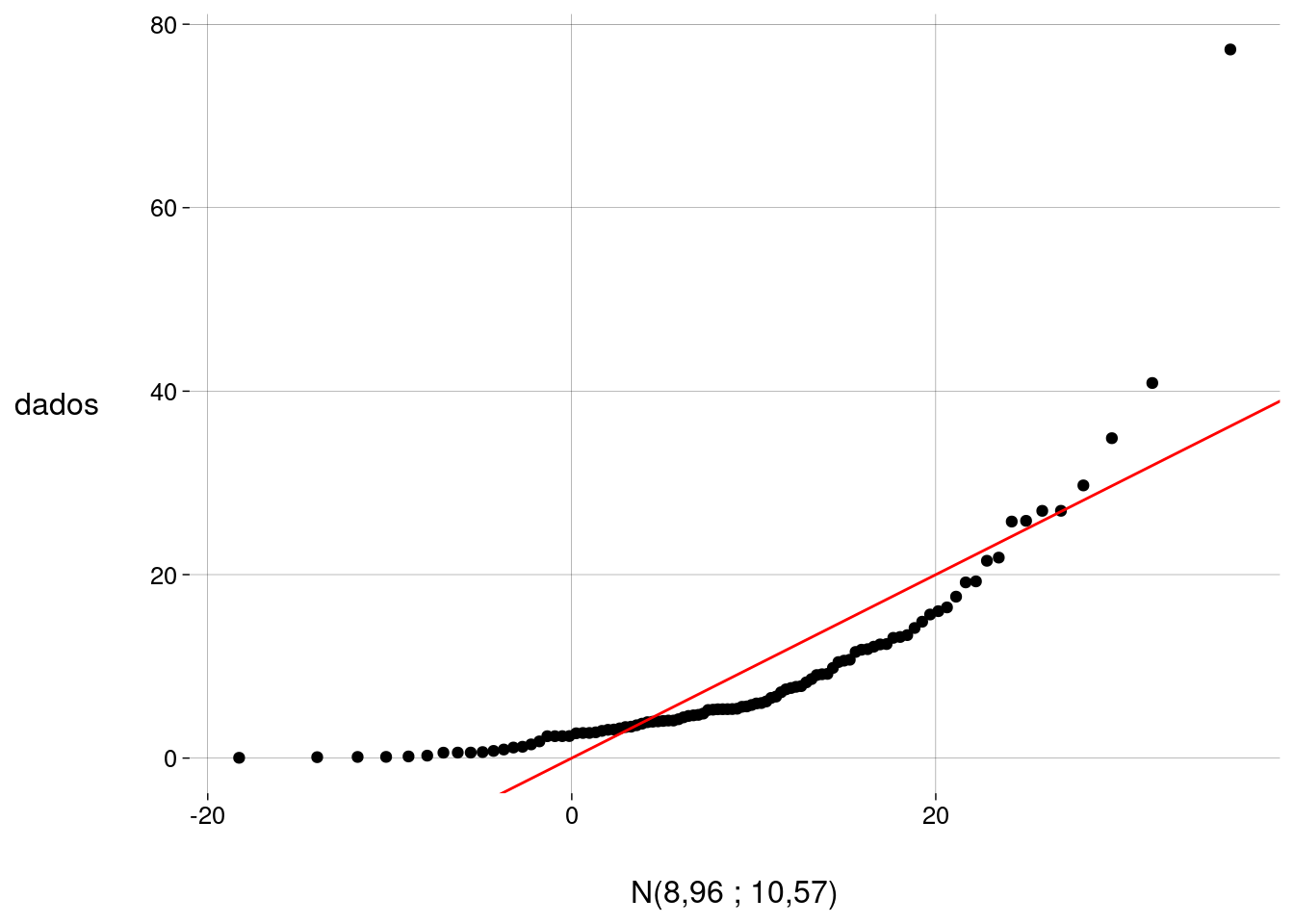
• Exercício: gere um gráfico quantil-quantil para estes dados, usando a distribuição exponencial com média \(10\) como distribuição teórica no eixo \(x\).

10.3.5 Aproximação da binomial pela normal

• Exemplo:

  • Uma organização vai receber sangue de \(32\) mil doadores escolhidos ao acaso.

  • A probabilidade de um doador ter sangue tipo O- é \(p = 0{,}06\).

  • Qual a probabilidade de a organização conseguir no mínimo \(1.850\) doadores com sangue do tipo O-?

• Cada doador é uma prova de Bernoulli, com probabilidade de sucesso \(p = 0{,}06\). Supondo que os doadores são independentes (por exemplo, não são todos parentes) e usando a distribuição binomial, a resposta é \[ \text{Binom}(X \geq 1850 \mid n = 32000, p = 0.06) \]

• Em R

pbinom(
  q = 1849,
  size = 32000,
  prob = 0.06,
  lower.tail = FALSE
)

## [1] 0,9521106

• Este resultado é o valor da longa e trabalhosa expressão \[ {32000 \choose 1850} 0{,}06^{1850} 0{,}94^{30150} + {32000 \choose 1851} 0{,}06^{1851} 0{,}94^{30149} + \cdots + {32000 \choose 32000} 0{,}06^{32000} 0{,}94^{0} \]

• Felizmente, podemos usar a distribuição normal para achar uma aproximação:

  • A média da distribuição binomial é \(np = 32.000 \cdot 0{,}06 = 1920\).

  • O desvio-padrão da distribuição binomial é \(\sqrt{np(1-p)} \approx 42{,}48\).

  • Usando uma normal com esta média e este desvio-padrão, temos

pnorm(
  q = 1849,
  mean = 1920,
  sd = 42.48,
  lower.tail = FALSE
)

## [1] 0,9526762

• As distribuições são mesmo parecidas:

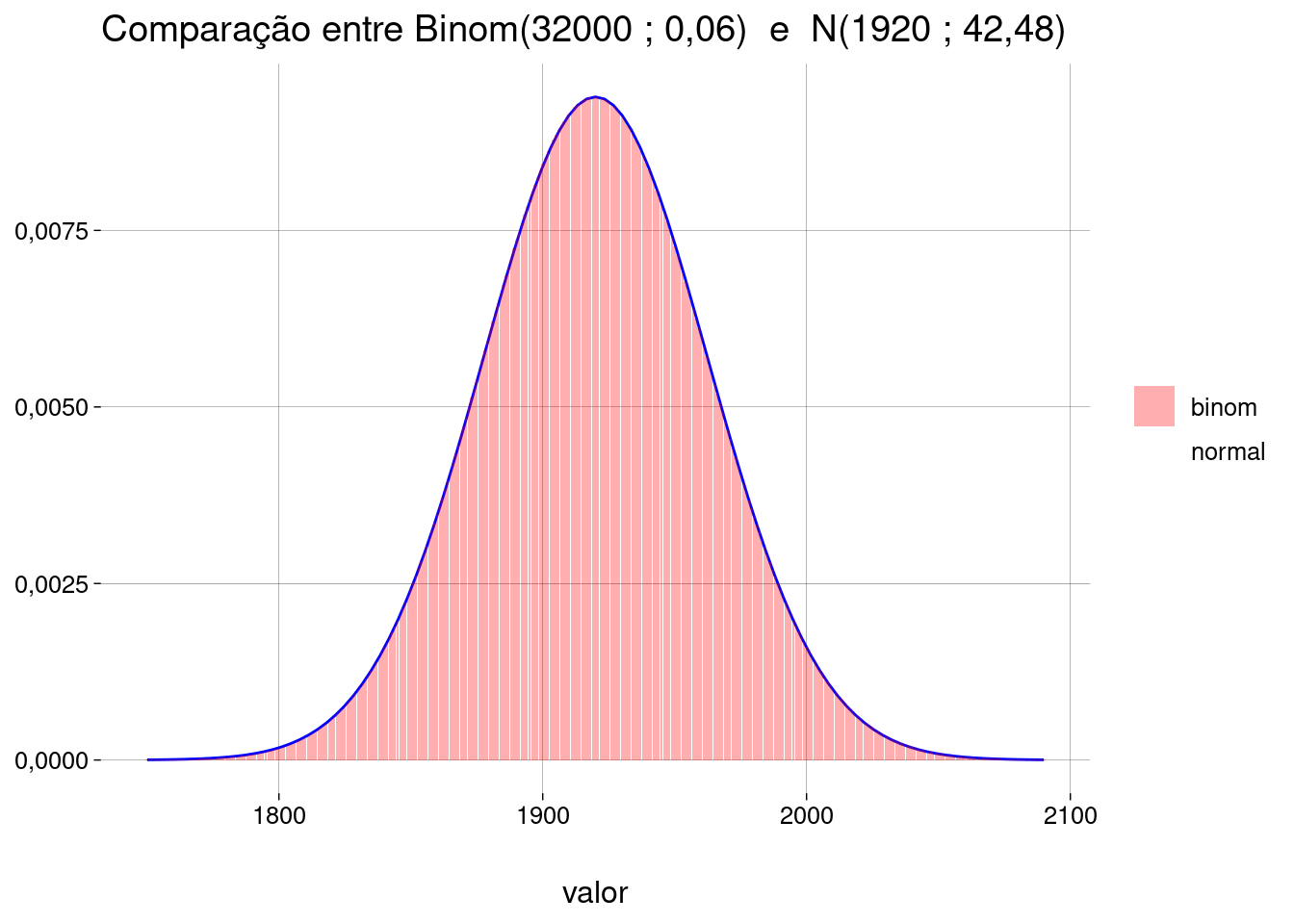
• Mas nem toda binomial se parece com uma normal:

n <- 5
p <- .1
normal_binom(n, p, limites = c(-2, 5)) + 
  scale_x_continuous(breaks = -2:5)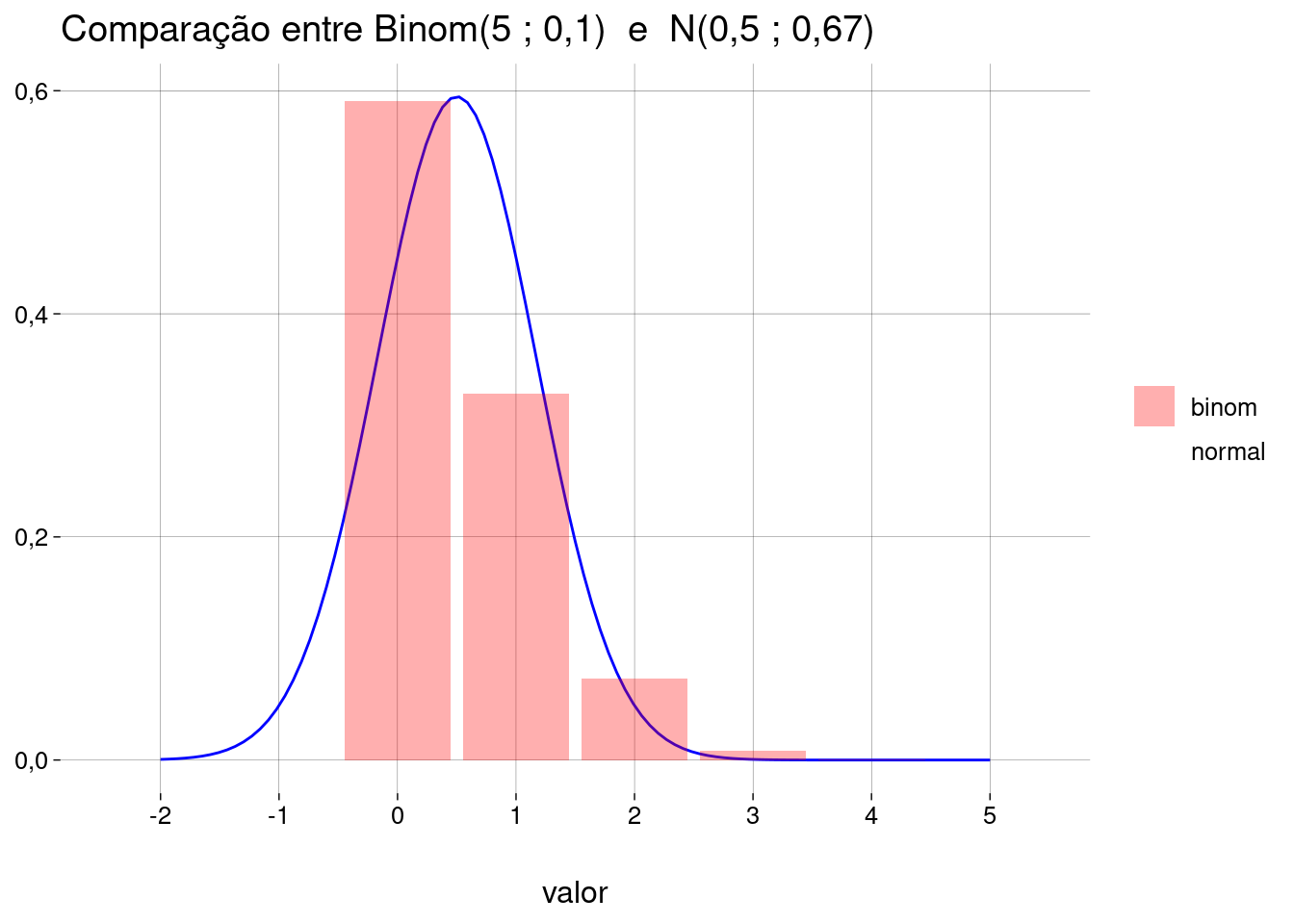

• Neste exemplo, quanto da probabilidade da normal está em valores abaixo de \(-0.5\) (valores que não fazem sentido para a binomial!)?

pnorm(-.5, n * p, sqrt(n * p * (1 - p)))

## [1] 0,06801856

• Como resolver isto?

• Lembrando que \(99{,}7\%\) da probabilidade da distribuição normal está a \(3\) desvios-padrão de distância da média, podemos exigir que a distribuição binomial esteja dentro destes limites.

• Então, a normal deve ser \(\mathcal{N}(\mu, \sigma)\) tal que o intervalo de \(\mu - 3\sigma\) até \(\mu + 3\sigma\) só tenha valores positivos.

• Ou seja, queremos \[\mu - 3\sigma > 0\]

• O que equivale a \[\mu > 3\sigma\]

• Como a normal é calculada a partir de \(\text{Binom}(X \mid n, p)\), isto equivale a \[ np > 3 \sqrt{np(1-p)} \]

• Elevando os dois lados ao quadrado: \[n^2p^2 > 9np(1-p)\]

• Dividindo ambos os lados por \(np\) (que é positivo): \[np > 9(1-p)\]

• Como \((1-p) \leq 1\), podemos nos satisfazer com \[np > 9\]

• Conclusão:

  • Para aproximar a binomial \(\text{Binom}(X \mid n, p)\) por uma normal, exigimos que \(np\) seja pelo menos \(10\).

  • Como a normal é simétrica, também exigimos que \(n(1-p)\) também seja pelo menos \(10\).

  • Em outras palavras, o número esperado de sucessos e o número esperado de fracassos precisam ser, ambos, maiores ou iguais a \(10\).

10.3.6 Correção de continuidade

• E se, no exemplo dos doadores de sangue, quiséssemos calcular a probabilidade de a organização obter exatamente \(1.850\) doadores com sangue O-?

dbinom(1850, 32000, .06)

## [1] 0,002420205

• Usando a aproximação normal, como calcularíamos esta probabilidade? Como a normal é uma distribuição contínua, \(P(X = 1850)\) é igual a zero (como qualquer probabilidade pontual)!

• A solução é calcular \(P(1849{,}5 \leq X \leq 1850{,}5)\):

probs <- pnorm(
  c(1849.5, 1850.5), 
  mean = 32000 * 0.06,  
  sd = sqrt(32000 * 0.06 * (1 - 0.06))
)

probs[2] - probs[1]

## [1] 0,002416361

• Trabalhando com uma distribuição \(\text{Binom}(X \mid n = 20, p = 0{,}5)\), isto fica claro no gráfico. Cada barra centrada no valor \(x\) compreende uma região de \(x - 0{,}5\) até \(x + 0{,}5\):

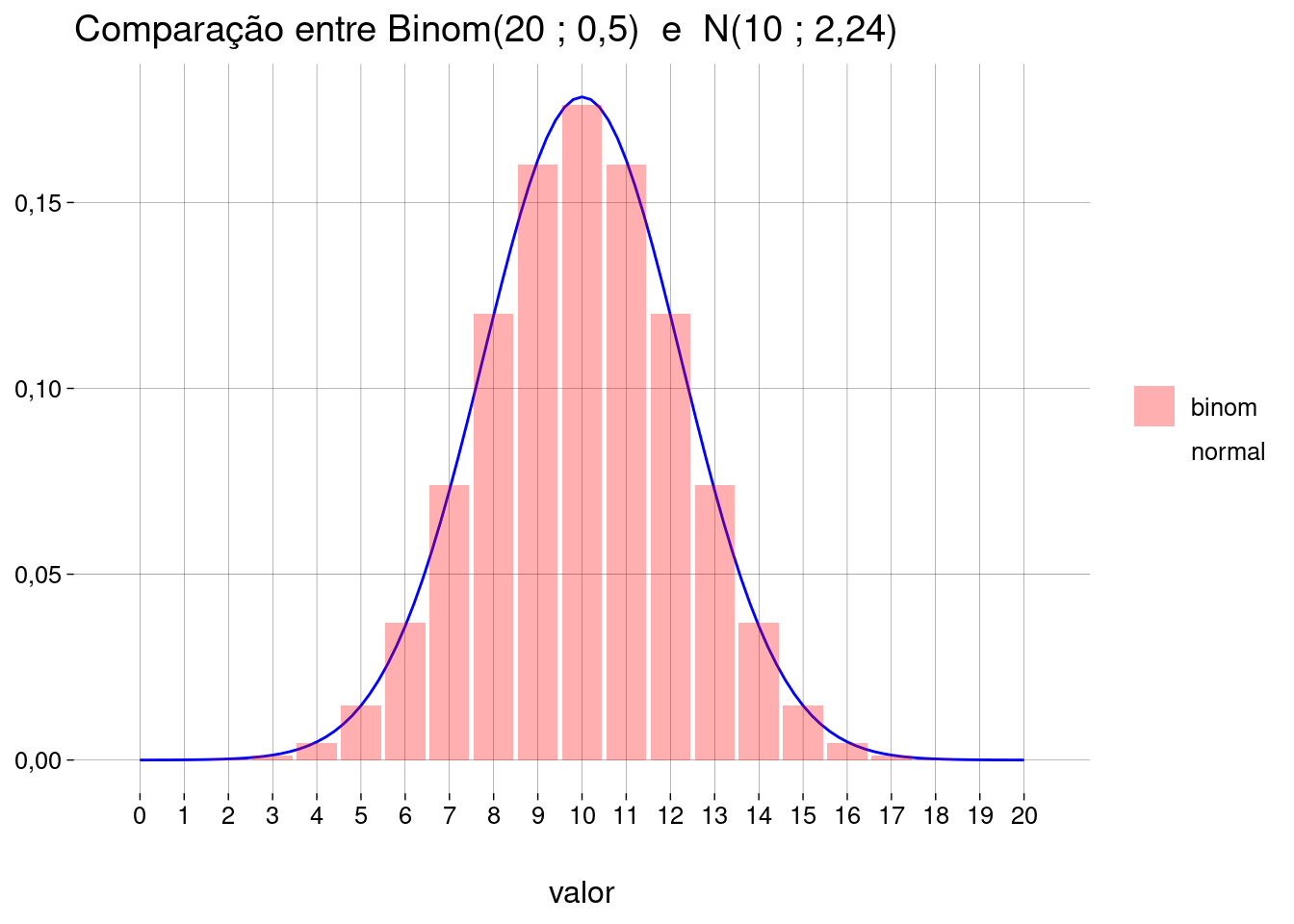
10.4 Exponencial

10.4.1 Exemplo

• Lembre-se de que a distribuição de Poisson modela o número de ocorrências de um fenômeno que tem uma média de \(\lambda\) ocorrências por período de tempo.

• Imagine que o números de visitas por minuto à sua página web é \(\lambda = 4\).

• Então, o tempo entre visitas é uma variável aleatória contínua \(X\), que pode ser modelada pela distribuição exponencial com média \(1/\lambda = 1/4 = 0{,}25\).

• Qual a probabilidade de que o tempo entre uma visita e a próxima seja menor do que \(0{,}33\) minuto? \[ \begin{aligned} P(X \leq 0{,}33 \mid \lambda = 4) &= \int_0^{0{,}33} \lambda e^{-\lambda \cdot 0{,}33} dx \\ &= 1 - e^{-\lambda \cdot 0{,}33} \\ &= 1 - e^{-1{,}32} \\ &\approx 0{,}73 \end{aligned} \]

10.4.2 No geral

• \(X \sim \text{Exp}(\lambda)\)

• Média: \(1/\lambda\)

• Desvio padrão: \(1/\lambda^2\)

• Suporte: \([0, \infty)\)

• Fdp: \[ f(x \mid \lambda) = \lambda e^{-\lambda x} \]

10.4.3 Em R

• Densidade: dexp(x, rate = 1)

• Probabilidade acumulada: pexp(q, rate = 1, lower.tail = TRUE)

• Quantil: qexp(p, rate = 1, lower.tail = TRUE)

• Geração de números aleatórios: rexp(n, rate = 1)

10.5 Outras distribuições contínuas importantes

• Distribuição \(t\) de Student

• Distribuição \(\chi^2\)

• Distribuição \(F\)

10.6 Jardim zoológico de distribuições

Para sua diversão: https://ben18785.shinyapps.io/distribution-zoo/