Capítulo 13 Testes de hipóteses

13.1 Vídeo 1

13.2 Testes de hipóteses sobre a proporção

13.2.1 Exemplo: proporção de bebês do sexo masculino

Um estudo de 1994 feito em Punjab, na Índia, relata que $56{,}9\%$ dos $550$ bebês nascidos em um ano em uma maternidade da região eram do sexo masculino.
Segundo estudos anteriores, $51{,}7\%$ dos bebês nascidos por ano nessa região são meninos.
Agora que a população tem acesso a exames que determinam o sexo do feto durante a gravidez, existem suspeitas de que fetos do sexo feminino estão sendo abortados pelos pais, por motivos culturais.
A evidência é suficiente para afirmar que a proporção de bebês meninos na maternidade do estudo é maior do que a proporção da região?

Hipóteses

Um teste de hipóteses sempre vai ter duas hipóteses.
A primeira hipótese é a apresentada como “padrão”. Esta é a hipótese que vai ser “desafiada”. O nome técnico para esta hipótese é hipótese de nulidade, ou hipótese nula. A hipótese de nulidade sempre envolve uma igualdade. e costuma ser chamada $H_0$. No exemplo,

\[ H_0 : p = 0{,}517 \]

Ou seja, a proporção de meninos nascidos na maternidade do estudo é de $51{,}7\%$, como no restante da região.
A segunda hipótese, chamada hipótese alternativa, contradiz de alguma maneira a hipótese de nulidade. No exemplo, vamos trabalhar com

\[ H_A : p > 0{,}517 \]

Ou seja, a verdadeira proporção de meninos nascidos na maternidade do estudo é maior que $51{,}7\%$.

Condições

O teste de hipóteses também se baseia no TCL.
Precisamos verificar as condições:
1. Independência: os sexos dos bebês são independentes entre si? Vamos supor que sim.
2. Amostra aleatória e representativa: a amostra são os $550$ bebês nascidos na maternidade em questão. Não vamos poder generalizar nossas conclusões para outras maternidades, nem outras regiões. Na verdade, a população consiste em todos os bebês nascidos nessa maternidade, nesse e em outros anos. Vamos supor que os números desse ano são compatíveis com os números de outros anos.
3. Tamanho da amostra: temos mais do que $30$ elementos, e a amostra é menor do que $10\%$ da população.
4. Quantidades de sucessos e fracassos potenciais: considerando meninos como sucesso, a hipótese de nulidade diz que deveria haver $550 \times 0{,}517 = 284{,}35$ sucessos e $550 \times 0{,}483 = 265{,}65$ fracassos na amostra, mais do que os $10$ exigidos.

Valores

Tamanho da amostra: $n = 550$
Proporção amostral: $\hat p = 0{,}57$
Hipótese de nulidade: $H_0 : p = 0{,}517$
Hipótese alternativa: $H_A : p > 0{,}517$
Nível de confiança: como com os intervalos de confiança, escolhemos $0{,}95$. Mas, em testes de hipóteses, trabalhamos com $1 - 0{,}95 = 0{,}05$ e chamamos este valor de nível de significância, escrito $\alpha = 0{,}05$.

Estratégia

Sempre começamos supondo que $H_0$ é verdadeira. No exemplo, isto significa supor que $p = 0{,}517$.
Com isso, construímos a distribuição amostral de $\hat p$, que vai ter como média o valor suposto de $p$.
Usando esta distribuição amostral, calculamos a probabilidade de obter uma amostra como a que obtivemos (com $\hat p = 0{,}569$) ou mais extrema (com $\hat p > 0{,}569$).
A probabilidade calculada é chamada de valor $p$.
Se o valor $p$ for muito baixo, isto indica que, supondo $H_0$, nossa amostra é muito improvável e serve como evidência contra $H_0$. Dizemos, então, que rejeitamos $H_0$.
Se o valor $p$ for alto, isto indica que, supondo $H_0$, nossa amostra não tem nada de inesperado, e não é evidência contra $H_0$. Não podemos rejeitar $H_0$.
“Baixo” ou “alto” são definidos em função do nível de significância $\alpha$.

A distribuição amostral de $\hat p$, supondo $H_0$

Pelo TCL e supondo $H_0$, a distribuição amostral das proporções vai ser normal, com média $\mu = p = 0{,}52$ e erro-padrão

\[ \sigma_{\hat p} = \sqrt{\frac{p(1-p)}{n}} = 0{,}02 \]
Graficamente:

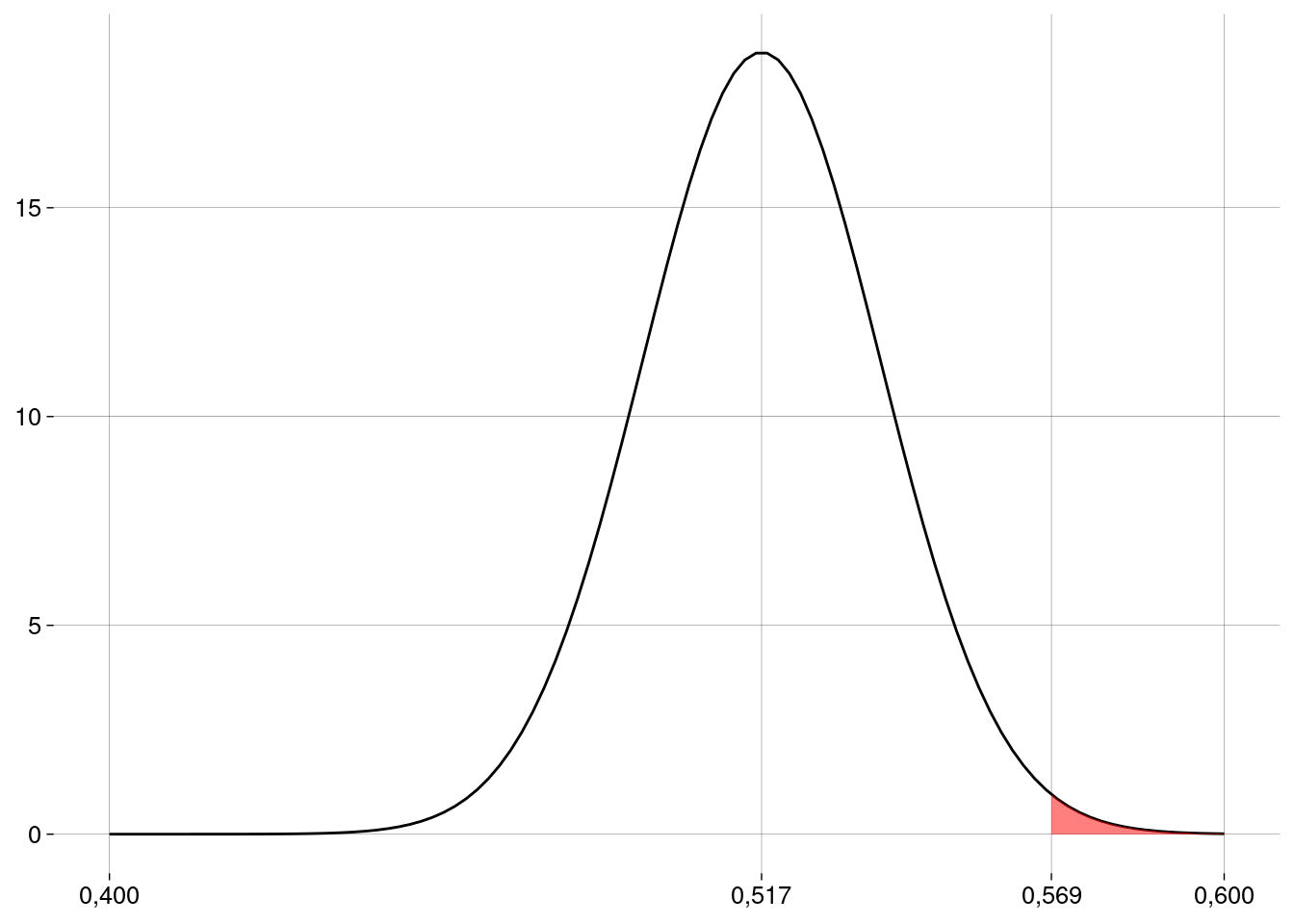
O valor $p$ e a conclusão

O valor $p$ vai ser a probabilidade que corresponde à área em vermelho, que pode ser calculada em R:

n <- 550
p_chapeu <- 0.569
p0 <- 0.517
ep <- sqrt(p0 * (1 - p0) / n)
valor_p <- pnorm(p_chapeu, mean = p0, sd = ep, lower.tail = FALSE)
valor_p

## [1] 0,007334952

Este valor é muito menor do que $\alpha = 0{,}05$. Logo, nossa amostra é evidência para rejeitar a hipótese de nulidade neste nível de significância. Concluímos que essa maternidade tem uma proporção de nascimentos de meninos maior do que $0{,}52$, com $\alpha = 0{,}05$.
Outros níveis de significância usados na prática são $\alpha = 0{,}1$ (menos exigente) e $\alpha = 0{,}01$ (mais exigente). Em algumas áreas, como na Física, são usados níveis de significância mais exigentes ainda, como $\alpha = 0{,}0000003$ no experimento que confirmou a existência do bóson de Higgs.

Em R

prop.test(
  x = p_chapeu * n,          # número de sucessos
  n = n,                     # tamanho da amostra
  p = p0,                    # valor de p na hipótese de nulidade
  alternative = 'greater',   # hipótese alternativa é p > p0
  conf.level = .95,          # 1 - α (o default já é .95)
  correct = FALSE            # sem correção de continuidade 
)

## 
##  1-sample proportions test without continuity correction
## 
## data:  p_chapeu * n out of n, null probability p0
## X-squared = 5,9557, df = 1, p-value = 0,007335
## alternative hypothesis: true p is greater than 0,517
## 95 percent confidence interval:
##  0,5340128 1,0000000
## sample estimates:
##     p 
## 0,569

13.2.2 Exemplo: percepção extra-sensorial

Um suposto vidente alega que consegue detectar os naipes de cartas colocadas viradas para baixo, diante dele, em uma mesa.
Em um experimento, um pesquisador apresenta ao suposto vidente $50$ cartas, escolhidas ao acaso dentre as cartas de $10$ baralhos, e o suposto vidente acerta o naipe de $10$ delas.
O pesquisador diz ao suposto vidente que ele teve menos acertos do que se ele tivesse adivinhado ao acaso: $50 \times 1/4 = 12{,}50$.
O suposto vidente diz que isso também é evidência dos seus poderes: os erros foram causados por “interferência”, pois o suposto vidente estava captando informações sobre o naipe da carta, mas não conseguiu interpretá-las corretamente.

Hipóteses

A hipótese de nulidade diz que o suposto vidente não tem poderes; a verdadeira proporção de acertos sempre vai ser, a princípio, $1/4$ da quantidade de cartas:

\[ p = 0{,}25 \]
A hipótese alternativa reflete os argumentos do suposto vidente de que uma proporção significativamente maior ou significativamente menor do que $25\%$ indica a existência de poderes extra-sensoriais:

\[ p \neq 0{,}25 \]
A hipótese alternativa, agora, vai gerar um teste bilateral.

Condições

Independência: Vamos supor que acertar o naipe de uma carta independe de acertar o naipe de outra carta. Por exemplo, podemos supor que a dificuldade de acertar o naipe de uma carta é sempre a mesma, independente da carta, da ordem em que elas aparecem etc. O fato de que as $50$ cartas foram escolhidas dentre $10$ baralhos ($520$ cartas, no total) nos permite considerar que os naipes das cartas escolhidas são independentes. Além disso, se não quisermos que o suposto vidente “conte” os naipes das cartas durante o experimento, podemos decidir só revelar os naipes das $50$ cartas depois que o suposto vidente tiver registrado seus palpites.
Amostra aleatória e representativa: A população é o conjunto de todas as cartas que poderiam ser escolhidas para o suposto vidente poder exercer seus poderes. As $50$ cartas, escolhidas ao acaso, representam de forma adequada esta população.
Tamanho da amostra: temos mais do que $30$ elementos, e a amostra é menor do que $10\%$ da população (que é infinita).
Quantidades de sucessos e fracassos potenciais: a hipótese de nulidade diz que deveria haver $50 \times 1/4 = 12{,}50$ sucessos e $50 \times 3/4 = 37{,}50$ fracassos na amostra, mais do que os $10$ exigidos.

Valores

Tamanho da amostra: $n = 50$
Proporção amostral: $\hat p = 0{,}20$
Hipótese de nulidade: $H_0 : p = 0{,}25$
Hipótese alternativa: $H_A : p \neq 0{,}25$
Nível de significância: $\alpha = 0{,}05$

Estratégia

Começamos supondo que $H_0$ é verdadeira: $p = 0{,}25$.
Com isso, construímos a distribuição amostral de $\hat p$, que vai ter como média o valor suposto de $p$.
Usando esta distribuição amostral, calculamos a probabilidade de obter uma amostra como a que obtivemos ou mais extrema (mais distante de $0{,}25$).

A distribuição amostral de $\hat p$, supondo $H_0$

Pelo TCL e supondo $H_0$, a distribuição amostral das proporções vai ser normal, com média $\mu = p = 0{,}25$ e erro-padrão

\[ \sigma_{\hat p} = \sqrt{\frac{p(1-p)}{n}} = 0{,}06 \]
Graficamente:

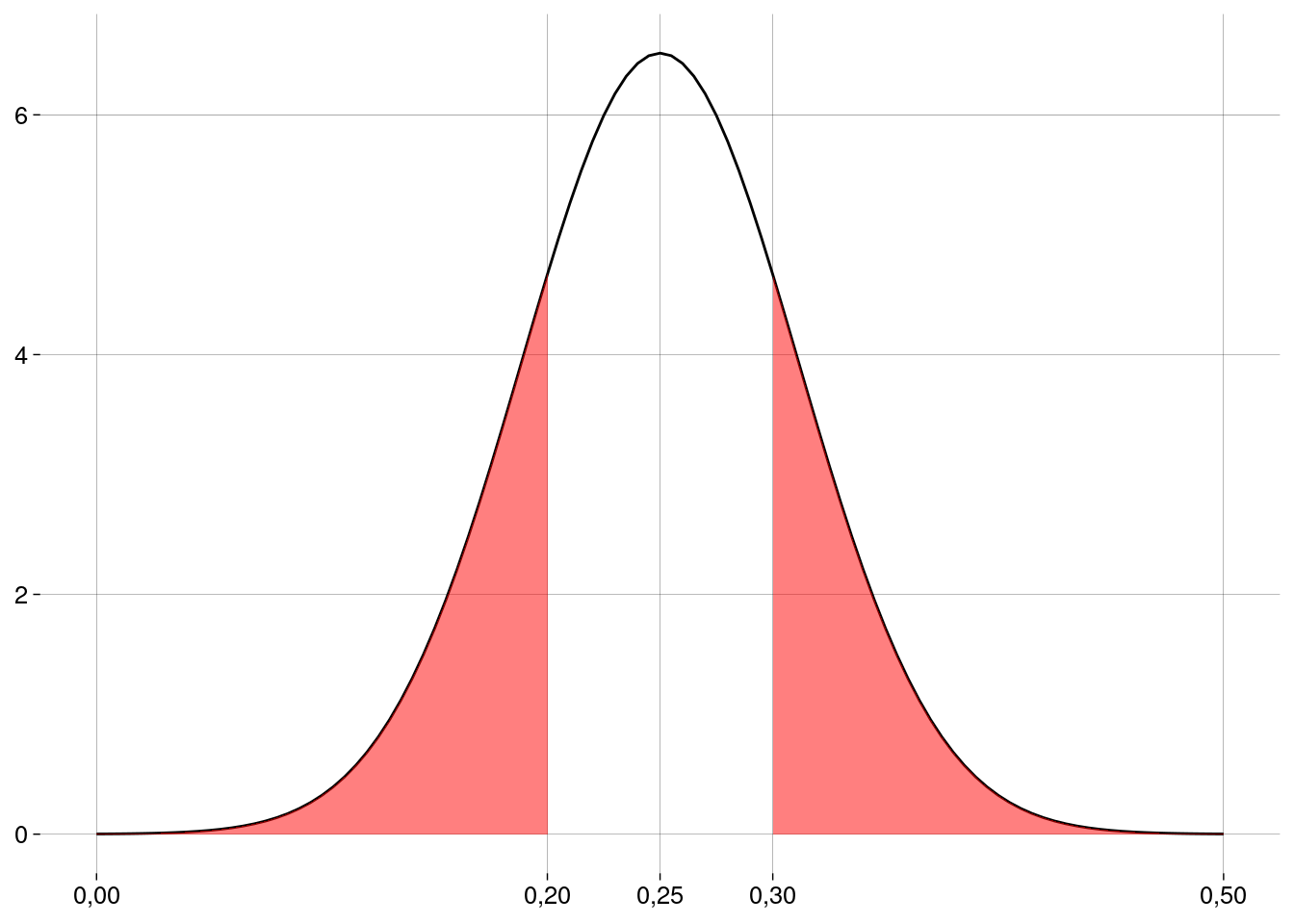
O valor $p$ e a conclusão

O valor $p$ vai ser a probabilidade que corresponde à área em vermelho, que pode ser calculada em R:

sucessos <- 10
n <- 50
p0 <- 1/4
p_chapeu <- sucessos / n
ep <- sqrt(p0 * (1 - p0) / n)
p_cauda_direita <- p0 + (p0 - p_chapeu)
valor_p <- 
  pnorm(p_chapeu, mean = p0, sd = ep) +
  pnorm(p_cauda_direita, mean = p0, sd = ep, lower.tail = FALSE)
valor_p

## [1] 0,4142162

Este valor é maior do que $\alpha = 0{,}05$. Logo, nossa amostra não é evidência para rejeitar a hipótese de nulidade neste nível de significância.

Em R

prop.test(
  x = sucessos,              # número de sucessos
  n = n,                     # tamanho da amostra
  p = p0,                    # valor de p na hipótese de nulidade
  alternative = 'two.sided', # hipótese alternativa é p != p0
  conf.level = .95,          # 1 - α (o default já é .95)
  correct = FALSE            # sem correção de continuidade 
)

## 
##  1-sample proportions test without continuity correction
## 
## data:  sucessos out of n, null probability p0
## X-squared = 0,66667, df = 1, p-value = 0,4142
## alternative hypothesis: true p is not equal to 0,25
## 95 percent confidence interval:
##  0,1124375 0,3303711
## sample estimates:
##   p 
## 0,2

13.2.3 Erros, poder e tamanho do efeito

Rejeitar $\times$ não rejeitar

Em um teste de hipóteses, nada é provado.
Se o valor $p$ for menor do que $\alpha$, você deve concluir que existem evidências para rejeitar a hipótese de nulidade.
Se o valor $p$ for maior do que $\alpha$, você deve concluir que não existem evidências para rejeitar a hipótese de nulidade.
Seja como for, você deve incluir na sua conclusão
- As hipóteses.
- O valor da estatística envolvida no teste (aqui, a proporção amostral).
- O tamanho da amostra.
- O valor de $\alpha$.
- O valor $p$.
- A informação de se o teste é unilateral ou bilateral.
Como nada é provado, existe a possibilidade de acontecer um erro:
- Você pode rejeitar $H_0$ quando ela é verdadeira, ou
- Você pode não rejeitar $H_0$ quando ela é falsa.

Erro tipo 1: rejeitar quando não devíamos

Falso positivo.
Diagnosticar como doente um paciente saudável.
Condenar um réu inocente.
Um erro tipo $1$ só acontece quando a hipótese de nulidade é verdadeira.
A probabilidade de um erro tipo $1$ acontecer é a probabilidade de a nossa amostra ser uma amostra “ruim”.
Mas a probabilidade de a amostra ser ruim é exatamente $\alpha$.
Então, a probabilidade de um erro tipo $1$ é sempre igual a $\alpha$.

Erro tipo 2: não rejeitar quando devíamos

Falso negativo.
Diagnosticar como saudável um paciente doente.
Absolver um réu culpado.
Um erro tipo $2$ só acontece quando a hipótese de nulidade é falsa.
Qual a probabilidade de um erro tipo $2$ acontecer? Vamos chamar esta probabilidade de $\beta$.
É difícil calcular $\beta$, porque a hipótese alternativa não fixa um valor para o parâmetro sendo testado; então, não sabemos qual distribuição amostral usar.
A probabilidade $\beta$ de um erro tipo $2$ diminui à medida que $\alpha$ aumenta.
Um $\alpha$ maior torna mais difícil rejeitar a hipótese de nulidade.

Poder de um teste

O “melhor” resultado do teste é rejeitar $H_0$ quando ela é falsa.
Isto acontece com probabilidade $1 - \beta$.
Este é o poder (ou potência) do teste: a capacidade de detectar a diferença entre o valor do parâmetro em $H_0$ e o valor verdadeiro do parâmetro.
Mas não é uma boa idéia aumentar $\alpha$ para aumentar o poder, pois isto aumenta a chance de um erro tipo $1$.
A melhor maneira de diminuir $\alpha$ e $\beta$ ao mesmo tempo é aumentando o tamanho da amostra.
Podemos calcular o tamanho da amostra necessário para que o poder do teste tenha um certo valor, mas isto depende de mais informação.

O tamanho do efeito

Diferença entre o valor do parâmetro em $H_0$ e o valor verdadeiro do parâmetro.
Efeitos maiores são mais fáceis de detectar.
Efeitos menores são mais difíceis de detectar.
O poder de um teste também depende do tamanho do efeito.

Explorando tudo interativamente

https://rpsychologist.com/d3/nhst/

13.2.4 Exercícios

Usando `binom.test`

No exemplo dos bebês, calcule a quantidade de nascimentos de meninos na amostra. O que há de estranho?

A função binom.test, de R base, também faz teste de hipótese para a proporção (embora usando um algoritmo diferente do nosso). Rode o seguinte código:

binom.test(
  x = p_chapeu * n,          # número de sucessos
  n = n,                     # tamanho da amostra
  p = p0,                    # valor de p na hipótese de nulidade
  alternative = 'greater',   # hipótese alternativa é p > p0
  conf.level = .95           # 1 - α
)

O que dá errado? Por quê? Como consertar?

Outro suposto vidente

O experimento do exemplo é repetido com outra pessoa, que acerta o naipe de $17$ das $50$ cartas. Refaça o teste de hipóteses com este novo valor, de duas maneiras:
1. Com um teste bilateral: $H_A : p \neq 0{,}25$.
2. Com um teste unilateral: $H_A : p > 0{,}25$.
Quais as suas conclusões?

13.3 Vídeo 2

13.4 Testes de hipóteses sobre a média

13.4.1 Exemplo: duração da gestação

O tempo de gestação em seres humanos segue a distribuição normal, com média $\mu = 280$ dias e desvio-padrão $\sigma = 10$ dias.
Em uma amostra de $n = 25$ bebês nascidos em uma clínica, o tempo médio de gestação foi de $\bar x = 275$ dias.
Esta amostra é evidência de que a duração média da gestação humana é diferente de $280$ dias?

Hipóteses

A hipótese de nulidade diz que a duração média da gestação é de $280$ dias:

\[ H_0 : \mu = 280 \]
A hipótese alternativa diz que duração média da gestação é diferente de $280$ dias:

\[ H_A : \mu \neq 280 \]

Condições

Verifique que as condições de independência, aleatoriedade, representatividade e tamanho da amostra são satisfeitas.
Como a distribuição da população é normal, podemos aceitar $n = 25$.

Valores

Tamanho da amostra: $n = 25$
Média amostral: $\bar x = 275$
Hipótese de nulidade: $H_0 : \mu = 280$
Hipótese alternativa: $H_A : \mu \neq 280$
Nível de significância: $\alpha = 0{,}05$

O valor $p$ e a conclusão

Como a hipótese alternativa envolve “$\neq$”, o teste é bilateral.
Já sabemos $\sigma$ (o desvio-padrão populacional). Não precisamos do desvio-padrão amostral.
A distribuição amostral vai ser a normal com média $\mu = 280$ e desvio-padrão

\[ EP = \frac{\sigma}{\sqrt{n}} = \frac{10}{\sqrt{25}} = 2 \]
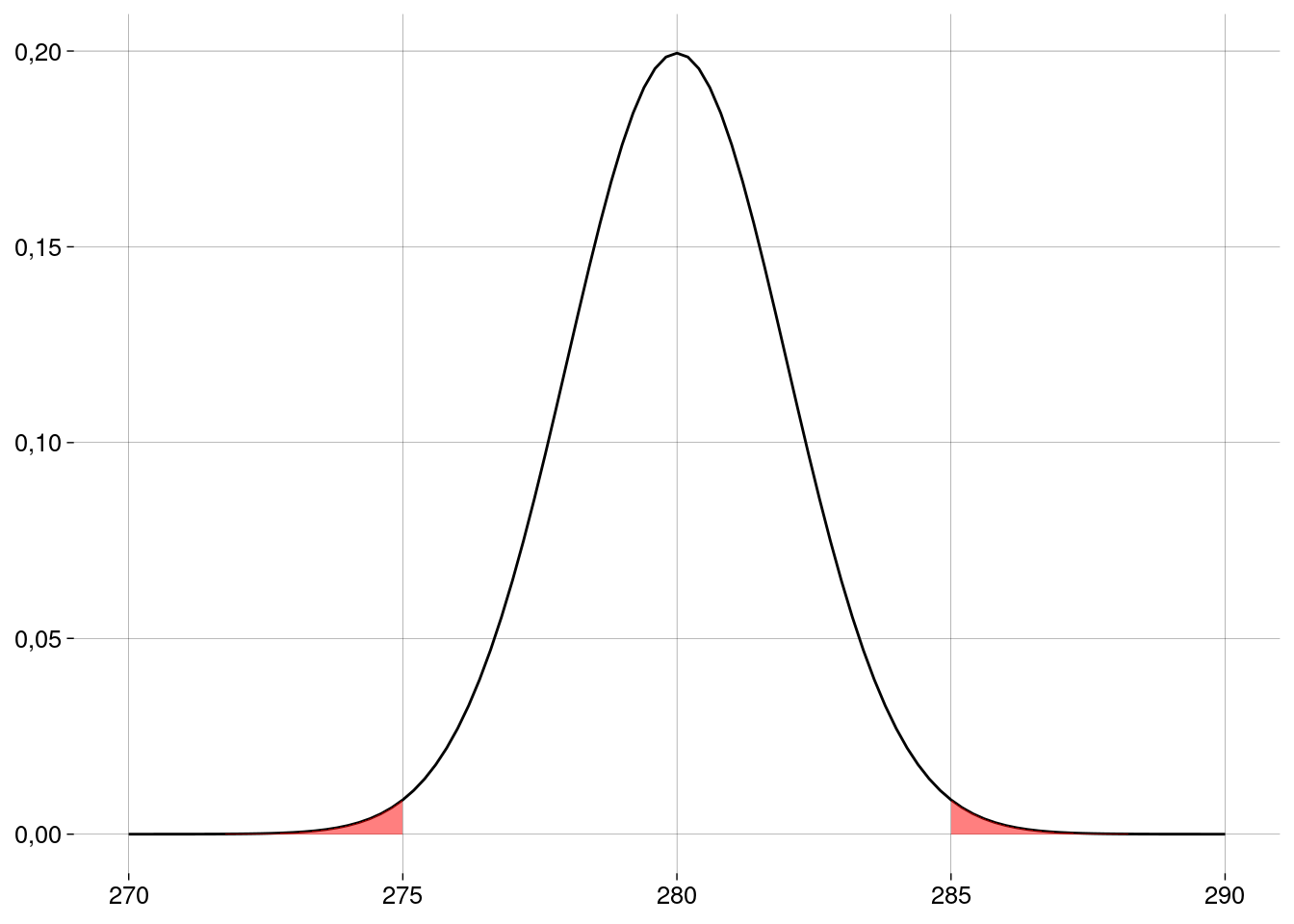
Usando esta distribuição amostral, calculamos a probabilidade de obter uma amostra como a que obtivemos (com a média amostral $5$ dias menor ou maior que a média suposta por $H_0$) ou mais extrema.
O valor $p$ vai ser esta probabilidade.

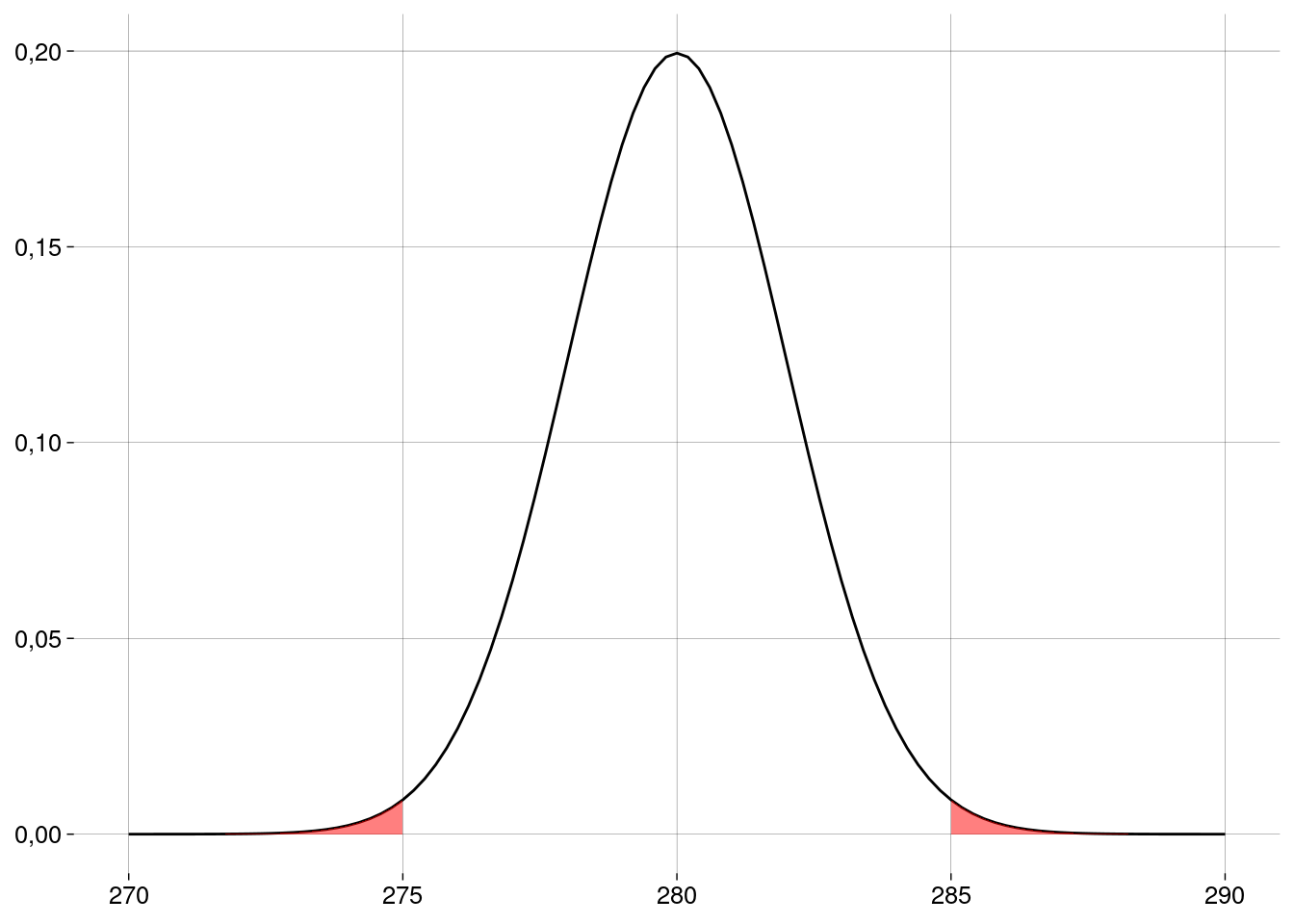
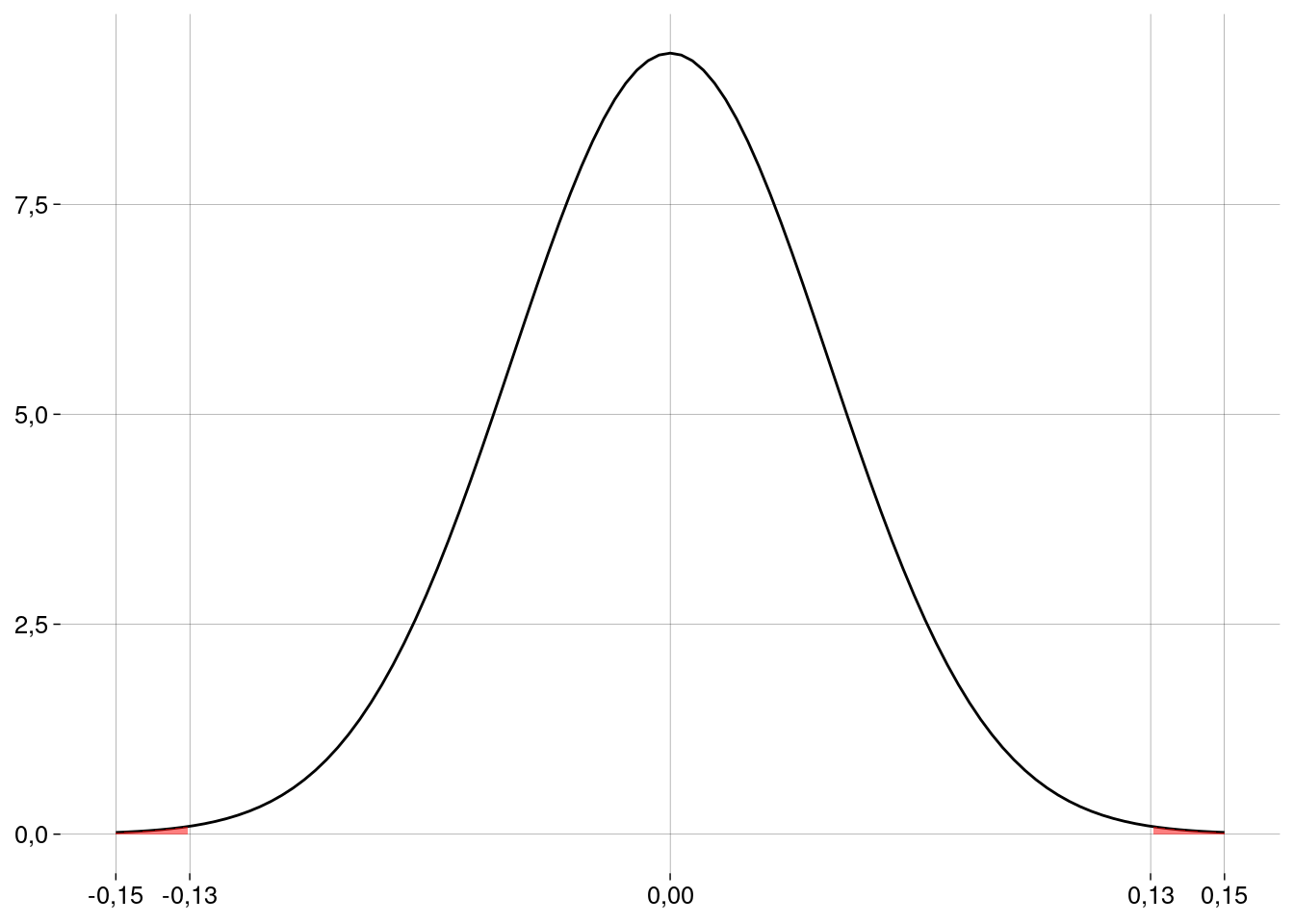
Calculando em R:

xbar <- 275
σ <- 10
n <- 25
ep <- σ / sqrt(n)
m0 <- 280
dif <- abs(m0 - xbar)
valor_p <- pnorm(xbar, m0, ep) +
  pnorm(m0 + dif, m0, ep, lower.tail = FALSE)
valor_p

## [1] 0,01241933

Este valor é menor do que $\alpha = 0{,}05$. Logo, nossa amostra é evidência para rejeitar a hipótese de nulidade neste nível de significância.
Pode parecer surpreendente que $5$ dias façam tanta diferença assim. O problema é que o desvio-padrão da população é relativamente baixo: $10$ dias. A variação é pequena. Por isso a diferença entre a média amostral e a média afirmada em $H_0$ é significativa.
Visto de outro modo: como $\sigma$ é um valor pequeno, o erro-padrão (i.e., o desvio-padrão da distribuição amostral) também é pequeno; a distribuição amostral, vista na figura acima, é bem estreita, com boa parte da probabilidade bem próxima da média.

Em R

Vamos carregar um pacote que implementa o teste z:
```
library(BSDA)
```

Esta função recebe o resumo (summary) da amostra:

zsum.test(
  mean.x = xbar, 
  sigma.x = σ, 
  n.x = n,
  alternative = 'two.sided',
  mu = m0
)

## 
##  One-sample z-Test
## 
## data:  Summarized x
## z = -2,5, p-value = 0,01242
## alternative hypothesis: true mean is not equal to 280
## 95 percent confidence interval:
##  271,0801 278,9199
## sample estimates:
## mean of x 
##       275

13.4.2 Exemplo: salmões novamente

Numa amostra de $150$ salmões, foi medida a concentração do contaminante mirex, um inseticida banido pela Convenção de Estocolmo.
As concentrações (em ppm) estão resumidas na tabela abaixo.
A média foi $\overline x = 0{,}09$ppm.
O desvio-padrão amostral foi $s = 0{,}05$ppm.
Não sabemos o desvio-padrão populacional.
Alguém nos diz que a concentração máxima de mirex permitida é de $0{,}08$ppm.
Esta amostra é evidência de que a concentração máxima foi ultrapassada?

Hipóteses

A hipótese de nulidade diz que a concentração é a máxima permitida ou menor:

\[ H_0 : \mu \leq 0{,}08 \]
A hipótese alternativa diz que a concentração máxima foi ultrapassada:

\[ H_A : \mu > 0{,}08 \]

Condições

Verifique que as condições de independência, aleatoriedade, representatividade e tamanho da amostra são satisfeitas.
Se precisar, reveja o vídeo sobre intervalos de confiança para a média, onde este exemplo também aparece.

Valores

Tamanho da amostra: $n = 150$
Média amostral: $\bar x = 0{,}09$
Hipótese de nulidade: $H_0 : \mu \leq 0{,}08$
Hipótese alternativa: $H_A : \mu > 0{,}08$
Nível de significância: $\alpha = 0{,}05$

O valor $p$ e a conclusão

Como não sabemos $\sigma$ (o desvio-padrão populacional), vamos usar $s$ (o desvio-padrão amostral).
Com isto, a distribuição amostral das médias será a distribuição $t$, com $n - 1 = 149$ graus de liberdade.
Mas, como a distribuição $t$ tem média $0$, precisamos padronizar a nossa média amostral: subtrair a média que $H_0$ diz ser a verdadeira ($\mu_0 = 0{,}08$) e dividir pelo erro-padrão:

\[ t_0 = \frac{\bar x - \mu_0}{EP} \]
O erro-padrão, como vimos nas aulas sobre intervalos de confiança, é

\[ EP = \frac{s}{\sqrt{n}} = \frac{0{,}05}{\sqrt{150}} = 0{,}00 \]
Isto nos dá

\[ t_0 = \frac{\bar x - \mu_0}{EP} = \frac{0{,}09 - 0{,}08}{0{,}00} = 2{,}80 \]
Como a hipótese alternativa envolve “$>$” e não “$\neq$”, o teste é unilateral.
O valor $p$ é a probabilidade de a média amostral padronizada ser maior do que $t_0$:

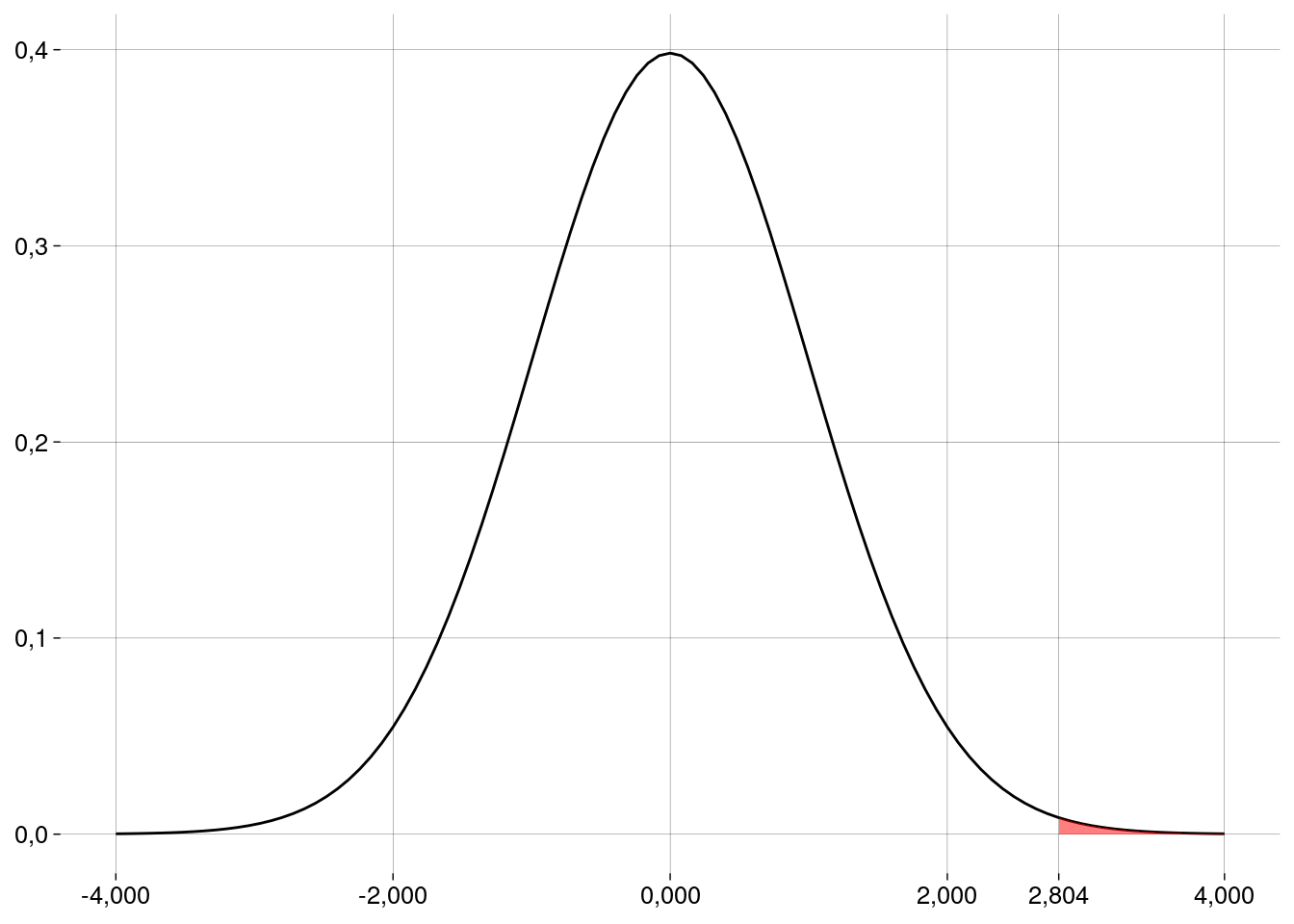
Este valor pode ser calculado em R (os valores da amostra estão em salmoes$mirex):

xbar <- mean(salmoes$mirex)
s <- sd(salmoes$mirex)
n <- length(salmoes$mirex)
ep <- s / sqrt(n)
m0 <- 0.08
t0 <- (xbar - m0) / ep
valor_p <- pt(t0, n - 1, lower.tail = FALSE)
valor_p

## [1] 0,002856456

Conclusão: como o valor $p$ é menor do que $\alpha$, rejeitamos a hipótese de nulidade. Com este nível de significância, a amostra é evidência de que a contaminação é maior do que a permitida.

Em R

t.test(
  salmoes$mirex, 
  alternative = 'greater',
  mu = m0
)

## 
##  One Sample t-test
## 
## data:  salmoes$mirex
## t = 2,8044, df = 149, p-value = 0,002856
## alternative hypothesis: true mean is greater than 0,08
## 95 percent confidence interval:
##  0,08464724        Inf
## sample estimates:
## mean of x 
##   0,09134

13.4.3 Relação entre testes e IC

Intervalos de confiança e testes de hipóteses são duas maneiras de enxergar a mesma inferência.

Lembre-se do exemplo sobre o tempo de gestação:

zt <- zsum.test(
  mean.x = xbar, 
  sigma.x = σ, 
  n.x = n,
  alternative = 'two.sided',
  mu = m0
)

zt

## 
##  One-sample z-Test
## 
## data:  Summarized x
## z = -2,5, p-value = 0,01242
## alternative hypothesis: true mean is not equal to 280
## 95 percent confidence interval:
##  271,0801 278,9199
## sample estimates:
## mean of x 
##       275

Mantenha fixa a nossa amostra de $25$ gestações.
A hipótese de nulidade foi rejeitada com $\alpha = 0{,}05$ porque o valor que ela “defendia” ($280$) estava fora do intervalo de confiança de $1 - \alpha = 0{,}95$.
Reciprocamente, mantendo $\alpha = 0{,}05$, qualquer hipótese de nulidade que não for rejeitada vai “defender” um valor dentro do intervalo de confiança (entre $271{,}08$ e $278{,}92$).
Experimente rodar a função zsum.test com diferentes valores de mu para verificar que isto acontece.

13.4.4 Explorando tudo interativamente (com outro app)

https://rpsychologist.com/pvalue/

13.4.5 Exercícios

Gestação

No exemplo, mude a hipótese alternativa para

\[ H_A : \mu < 280? \]
- Sem refazer os cálculos, você consegue dizer qual é o novo valor $p$? Compare-o com o valor $p$ original.
- A hipótese de nulidade continuaria sendo rejeitada?
- O que mudaria na chamada da função zsum.test?

Salmões

Qual seria o valor $p$ se a média amostral tivesse sido $0{,}08$ppm?
Qual seria o valor $p$ se as hipóteses fossem

\[ \begin{align*} H_0 &: \mu = 0{,}08 \\ H_A &: \mu \neq 0{,}08 \end{align*} \]

e a média amostral tivesse sido $0{,}08$ppm?
Quando o valor $p$ é $0$?

Testes e IC

O que acontece com o intervalo de confiança quando o teste de hipótese é unilateral?
Já que intervalos de confiança e testes de hipóteses contêm a mesma informação, qual dos dois procedimentos você acha mais intuitivo? Mais fácil de executar? Mais fácil de apresentar a um leigo?

App

Entre em https://rpsychologist.com/pvalue/
No “painel de controle”, deixe sample dist. statistic (estatística da distribuição amostral) em Mean (média). Com isto, a curva de baixo vai mostrar a distribuição amostral das médias.
Qual o efeito, sobre a distribuição amostral, de aumentar o tamanho da amostra? Por quê?
Defina o tamanho da amostra como $9$.
O app está configurado para o seguinte teste:

\[ \begin{align*} H_0 &: \mu = 100 \\ H_A &: \mu \neq 100 \end{align*} \]
Primeira situação: a hipótese de nulidade é verdadeira.
1. Faça o que você deve fazer para que, no app, $H_0$ seja verdadeira.
  Dica: a distribuição populacional “verdadeira” é representada pela curva de cima.
2. Retire $200$ amostras de $9$ elementos cada, apertando quatro vezes o botão +50.
3. Quantas das $200$ bolinhas são azuis? O que elas significam em termos de médias amostrais? Qual a relação delas com $\alpha$?
4. Mude sample dist. statistic para Z.
5. O que significam os novos rótulos no eixo horizontal da distribuição amostral?
6. O que significam as linhas pontilhadas verticais? Em que valores do eixo horizontal elas estão?
7. Se o app nos deixasse mudar essas linhas pontilhadas de posição (o app não deixa), o que isto significaria?
8. Mude sample dist. statistic para p-value. Agora, as $200$ amostras aparecem distribuídas de acordo com seus valores $p$.
9. O que significam as bolinhas azuis?
10. O que significam as bolinhas vermelhas?
11. Com $H_0$ verdadeira, como os valores $p$ das $200$ amostras estão distribuídos?
Segunda situação: a hipótese de nulidade é falsa.
1. Apague as amostras, clicando em CLEAR.
2. Mude sample dist. statistic para mean.
3. Defina o tamanho da amostra como $9$.
4. Faça o que você deve fazer para que a média populacional passe a ser aproximadamente $110$, tornando $H_0$ falsa.
5. Retire $200$ amostras de $9$ elementos cada, apertando quatro vezes o botão +50.
6. Qual fração aproximada das $200$ bolinhas são azuis? O que elas significam em termos de médias amostrais? Qual a relação delas com $1 - \beta$ (a potência)?
7. Você pode alterar o tamanho das amostras agora, e o app vai atualizar as figuras magicamente. Qual deve ser o valor de $n$ para que a potência ultrapasse $0{,}8$?
8. Mude sample dist. statistic para p-value.
9. O que significam as bolinhas azuis?
10. O que significam as bolinhas vermelhas?
11. Com $H_0$ falsa, como os valores $p$ das $200$ amostras estão distribuídos?
Terceira situação: a hipótese de nulidade é falsa, mas não muito.
1. Apague as amostras, clicando em CLEAR.
2. Faça o que você deve fazer para que a média populacional passe a ser aproximadamente $105$, tornando $H_0$ falsa, mas com uma diferença menor para a média verdadeira.
3. Refaça os passos restantes da segunda situação.
4. Comente os resultados.
Quarta situação: a hipótese de nulidade é falsa, e muito.
1. Apague as amostras, clicando em CLEAR.
2. Faça o que você deve fazer para que a média populacional passe a ser aproximadamente $120$, tornando $H_0$ falsa, com uma diferença muito grande para a média verdadeira.
3. Refaça os passos restantes da segunda situação.
4. Comente os resultados.
Desafio:
- A curva da parte superior da página, de onde “pingam” as médias amostrais, é uma distribuição normal.
- Durante os exercícios acima, você descobriu como alterar a média dessa normal.
- Você consegue calcular o desvio-padrão dessa normal?
  Dica: considere a fórmula que dá o erro-padrão da distribuição amostral (a curva de baixo).

13.5 Vídeo 3

13.6 Testes de hipóteses com duas amostras

13.6.1 Diferença entre proporções

Exemplo: jovens online

Duas amostras:

$141$ de $248$ rapazes com idades entre $15$ e $17$ anos possuem um perfil online.
$179$ de $256$ meninas com idades entre $15$ e $17$ anos possuem um perfil online.

A diferença entre as proporções é significativa?

Condições

As mesmas condições de testes com uma amostra precisam ser verificadas:
- Independência.
- Amostras aleatórias e representativas.
- Tamanho da amostra menor que $10\%$ da população.
E mais:
- Independência dos grupos.
- Cada grupo deve ter no mínimo $10$ sucessos e $10$ fracassos.

Hipóteses

O teste, agora, é sobre a diferença entre as proporções:

\[ H_0 : p_h - p_m = 0 \\ H_A : p_h - p_m \neq 0 \]

Erro padrão

A diferença $p_h - p_m$ é uma variável aleatória.
A variância da diferença é a soma das variâncias:

\[ \sigma^2_{p_h - p_m} = \sigma^2_{p_h} + \sigma^2_{p_m} \]
A variância da proporção amostral é

\[ \sigma^2(\hat p) = \frac{p(1 - p)}{n} \]
Logo, a variância da diferença $p_h - p_m$ será

\[ \sigma^2(\hat p_h - \hat p_m) = \frac{p_h(1 - p_h)}{n_h} + \frac{p_m(1 - p_m)}{n_m} \]
Daí, o desvio-padrão da distribuição amostral da diferença é

\[ \sigma(\hat p_h - \hat p_m) = \sqrt{\frac{p_h(1 - p_h)}{n_h} + \frac{p_m(1 - p_m)}{n_m}} \]
Como não sabemos os valores verdadeiros de $p_h$ e $p_m$, usamos as proporções amostrais para obter o erro-padrão:

\[ EP(\hat p_h - \hat p_m) = \sqrt{\frac{\hat p_h(1 - \hat p_h)}{n_h} + \frac{\hat p_m(1 - \hat p_m)}{n_m}} \]
Se fôssemos construir um intervalo de confiança, usaríamos este erro-padrão.
Mas, em um teste de hipóteses, estamos supondo que $H_0$ é verdadeira, o que equivale a dizer que $p_h = p_m$.
Então, podemos calcular uma proporção ponderada, ou agregada:

\[ \bar p = \frac{\text{sucessos}_h + \text{sucessos}_m}{n_h + n_m} \]
Aí, calculamos o erro-padrão com este valor em vez de $\hat p_h$ e $\hat p_m$:

\[ EP(\hat p_h - \hat p_m) = \sqrt{\frac{\bar p(1 - \bar p)}{n_h} + \frac{\bar p(1 - \bar p)}{n_m}} \]

Valores

Tamanhos das amostras: $n_h = 248$ e $n_m = 256$.
Proporções amostrais: $\hat p_h = 0{,}57$ e $\hat p_m = 0{,}7$.
Hipótese de nulidade: $H_0 : p_h - p_m = 0$.
Hipótese alternativa: $H_A : p_h - p_m \neq 0$.
Nível de significância: $\alpha = 0{,}05$.

Cálculos

n_h <- 248
sucessos_h <- 141
p_h <- sucessos_h / n_h

n_m <- 256
sucessos_m <- 179
p_m <- sucessos_m / n_m

d0 <- 0
d_chapeu <- p_m - p_h 
d_cauda_esquerda <- d0 - (d_chapeu - d0)

p_agregado <- (sucessos_h + sucessos_m) / (n_h + n_m)

ep <- sqrt(
  p_agregado * (1 - p_agregado) / n_h + 
  p_agregado * (1 - p_agregado) / n_m
)

ep

## [1] 0,04289659

A distribuição amostral de $\hat p_h - \hat p_m$, supondo $H_0$

Valor $p$ e conclusão

valor_p <- 
  pnorm(d_cauda_esquerda, mean = d0, sd = ep) +
  pnorm(d_chapeu, mean = d0, sd = ep, lower.tail = FALSE)
valor_p

## [1] 0,002317759

Este valor é menor do que $\alpha = 0{,}05$. Logo, nossa amostra é evidência para rejeitar a hipótese de nulidade neste nível de significância.

Em R

prop.test(
  x = c(sucessos_m, sucessos_h),
  n = c(n_m, n_h),
  alternative = 'two.sided',
  correct = FALSE
)

## 
##  2-sample test for equality of proportions without continuity correction
## 
## data:  c(sucessos_m, sucessos_h) out of c(n_m, n_h)
## X-squared = 9,2792, df = 1, p-value = 0,002318
## alternative hypothesis: two.sided
## 95 percent confidence interval:
##  0,04727054 0,21407019
## sample estimates:
##    prop 1    prop 2 
## 0,6992188 0,5685484

13.6.2 Diferença entre médias (amostras independentes)

Exemplo: olhos $\times$ flores

Em $2006$, pesquisadores em uma universidade inglesa fizeram um experimento para verificar se as pessoas alteram seu comportamento quando se sentem vigiadas.
Na universidade, havia uma copa onde chá, café e leite eram disponibilizados para todos que frequentavam o local.
Na parede, próximo às bebidas, ficava um cartaz com as instruções para pagamento e os valores de cada bebida. As pessoas deviam depositar o dinheiro em uma caixa próxima às bebidas.
Junto a esse cartaz, os pesquisadores afixaram outro, com imagens.
As imagens eram trocadas regularmente. Durante uma semana, eram flores; durante uma semana, era um par de olhos. Esta alternância foi mantida durante $10$ semanas.
A disposição da copa era tal que, se alguém decidisse não pagar, ninguém perceberia.
Os pesquisadores controlaram a arrecadação por litro de leite consumido por semana.
Em média, esta arrecadação foi quase $3$ vezes maior nas semanas em que o cartaz continha o par de olhos, em comparação com as semanas em que o cartaz continha as flores:

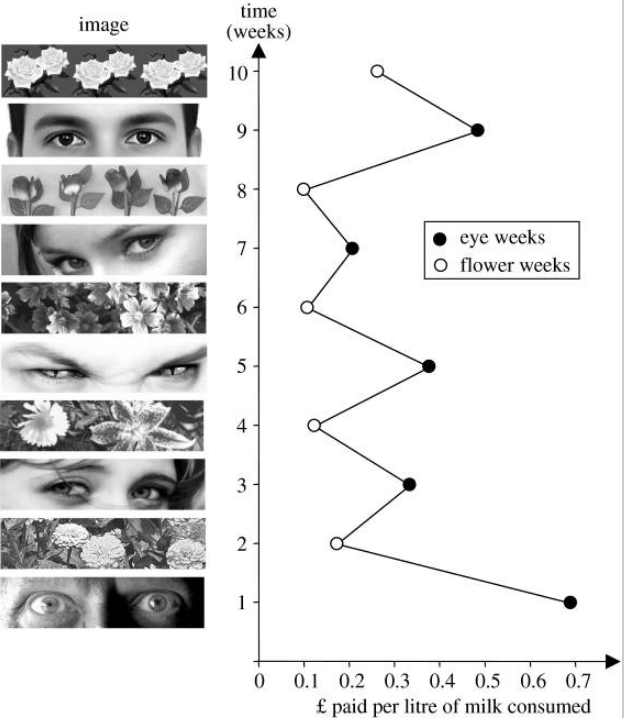
Este exemplo é baseado em https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1686213/, de onde foi retirada a imagem acima.

Amostras

As $5$ semanas com os cartazes dos olhos formam uma amostra.
Nessas semanas, a arrecadação média por litro de leite foi de $0{,}417$ libras, com desvio-padrão de $0{,}1811$.
As $5$ semanas com os cartazes das flores formam a outra amostra.
Nessas semanas, a arrecadação média por litro de leite foi de $0{,}151$ libras, com desvio-padrão de $0{,}067$.

Em R:

amostra_1 <- c(0.6843, 0.3038, 0.3780, 0.2202, 0.4987)
amostra_2 <- c(0.1737, 0.117, 0.1075, 0.0981, 0.2587)

Condições

Independência: vamos supor que as contribuições de uma pessoa são independentes das das outras.
Amostras aleatórias e representativas: vamos supor que essas contribuições representam a população de interesse (contribuições de frequentadores e funcionários da universidade? de todos os cidadãos ingleses? de toda a humanidade?)
Tamanho das amostras:
- As amostras são menos do que $10\%$ da população.
- As amostras são pequenas ($n_1 = n_2 = 5$). Precisamos ser cautelosos quanto às conclusões.
Independência dos grupos: o comportamento das pessoas nas semanas dos olhos é independente do comportamento das mesmas pessoas nas semanas das flores? Vamos supor que sim, embora esta seja uma suposição arriscada.
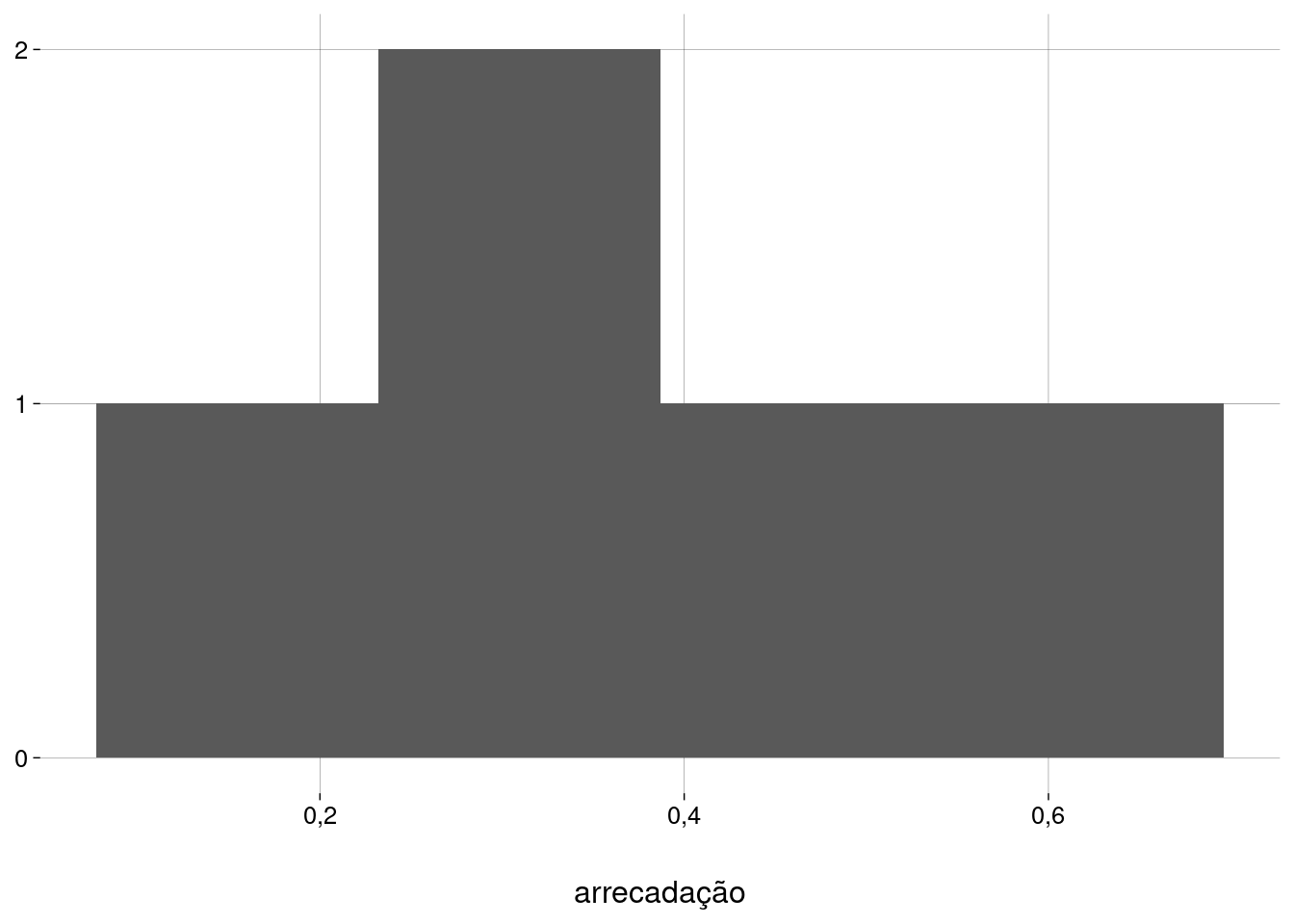
Dados aproximadamente normais: com amostras tão pequenas, é difícil avaliar.
- Para as semanas dos olhos:
- Para as semanas das flores:
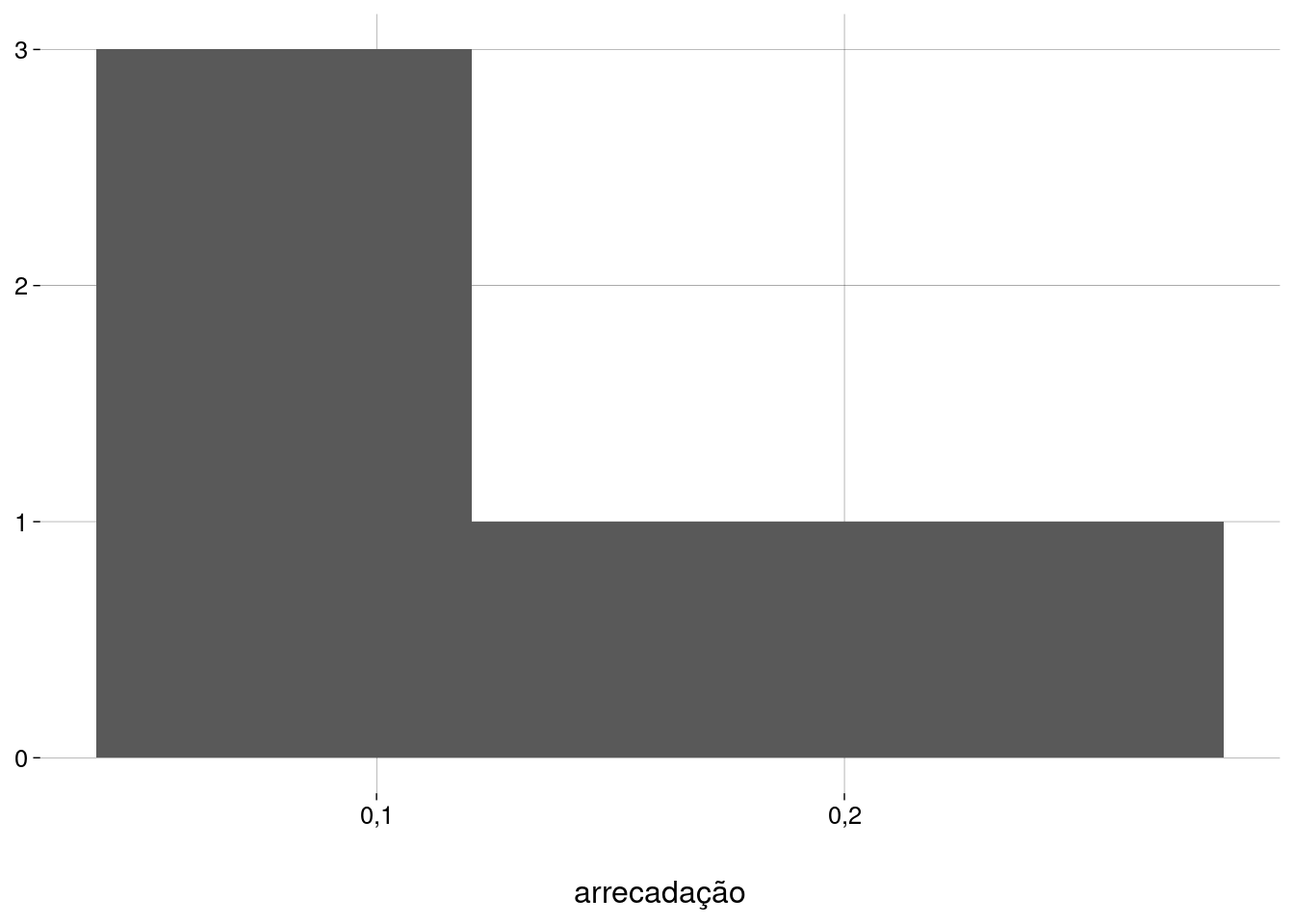
- Agregando as duas amostras:
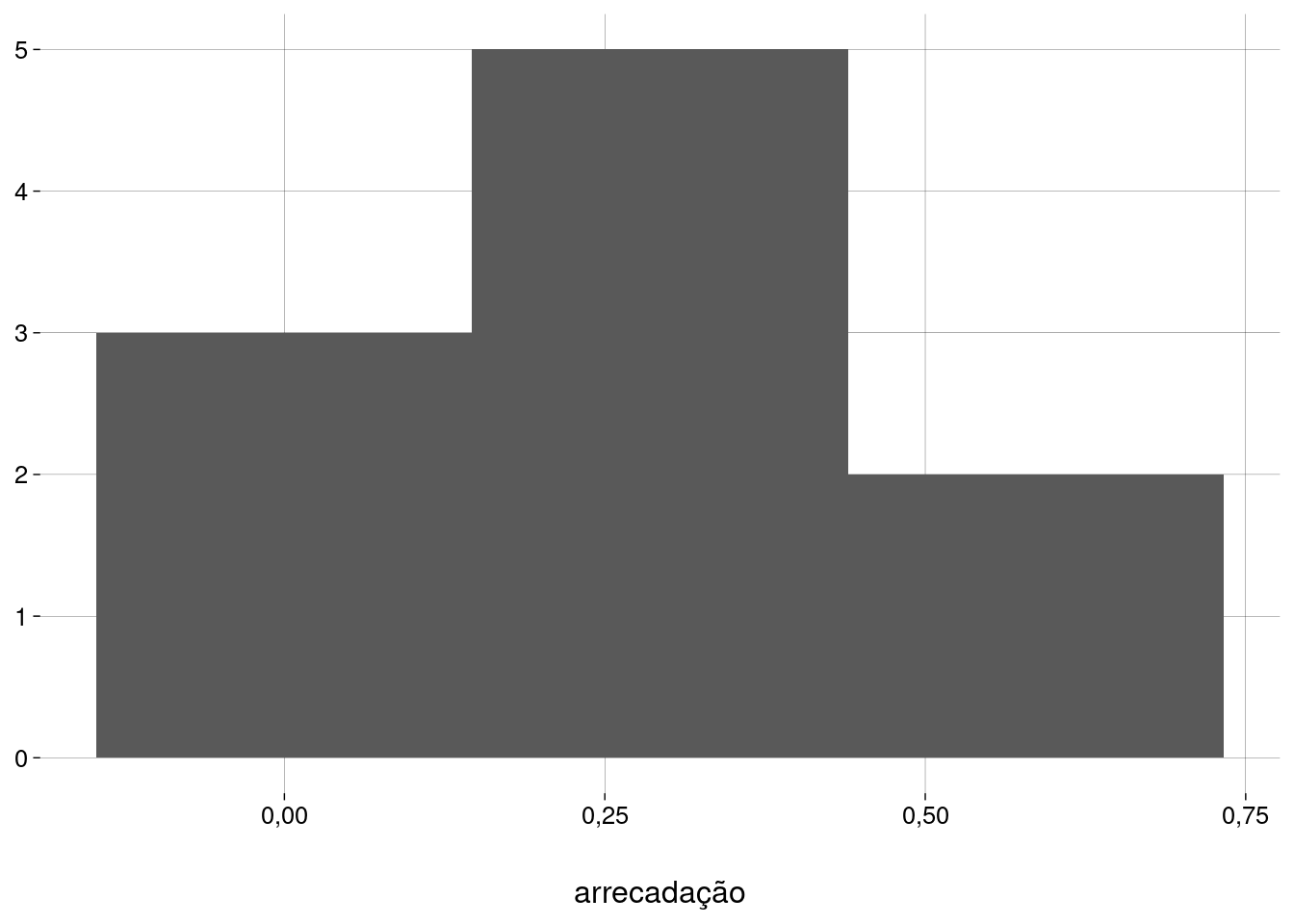
- Pelo menos o terceiro histograma (com a união das duas amostras) é unimodal e simétrico. Vamos prosseguir com cautela.

Hipóteses

O teste, agora, é sobre a diferença entre as médias:

\[ H_0 : \mu_1 - \mu_2 = 0 \\ H_A : \mu_1 - \mu_2 \neq 0 \]

onde $\mu_1$ é a média da arrecadação nas semanas dos olhos, e $\mu_2$ é a média da arrecadação nas semanas das flores.

Erro padrão (variâncias diferentes)

Mesmo quando supomos $H_0$ — i.e., que as médias populacionais $\mu_1$ e $\mu_2$ são iguais — não podemos afirmar nada sobre os desvios-padrão das duas subpopulações: as semanas dos olhos e as semanas das flores.
Podemos estimar as variações das duas amostras criando um boxplot:

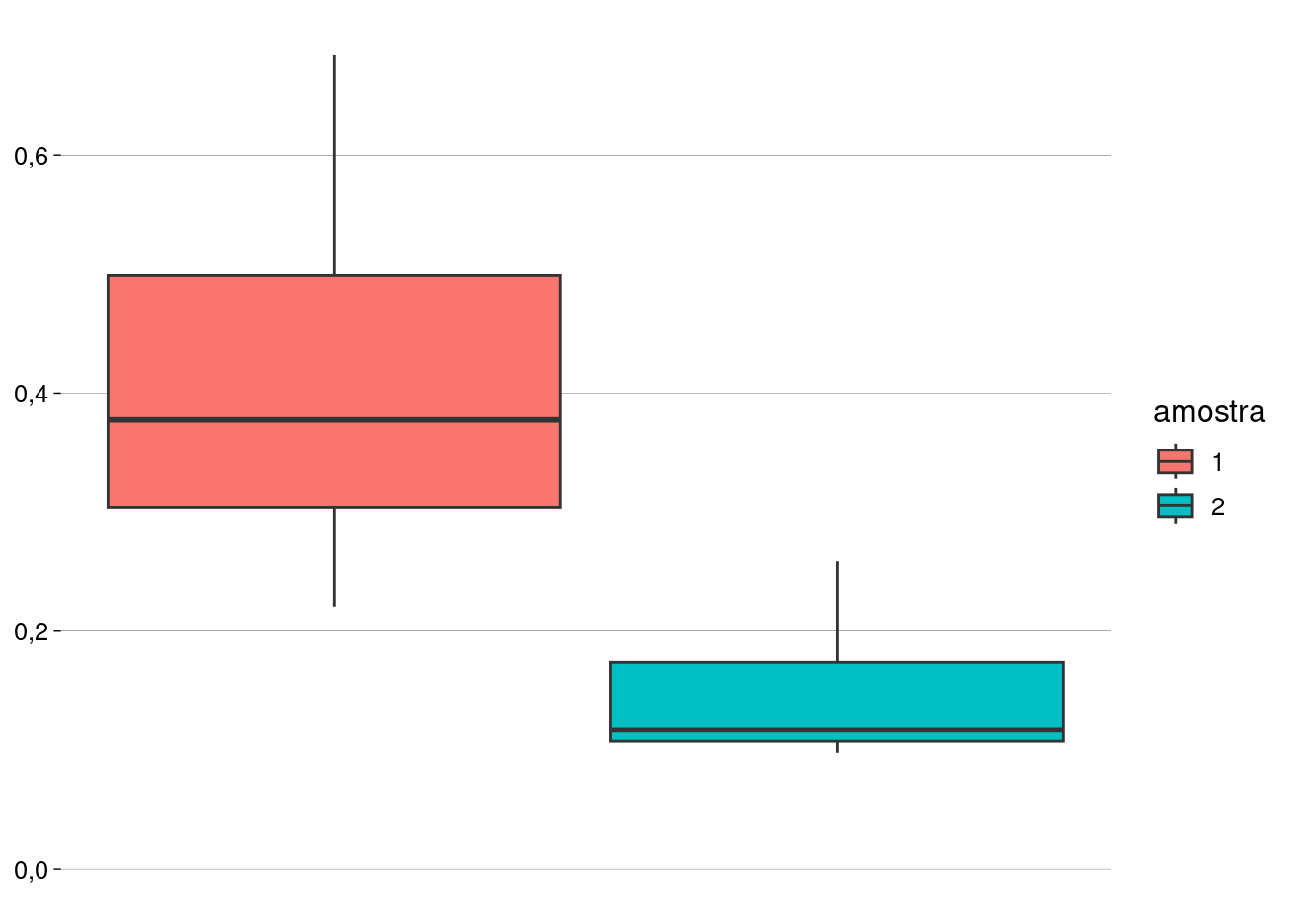
A amostra $1$ parece ter uma variação maior do que a amostra $2$.
De fato, o desvio-padrão da amostra $1$ é quase o triplo do da amostra $2$.
```
sd(amostra_1)
```
```
## [1] 0,1811006
```
```
sd(amostra_2)
```
```
## [1] 0,06700978
```
Então, estimamos a variância das semanas dos olhos por

\[ \hat \sigma^2_1 = \frac{s^2_1}{n_1} \]

e estimamos a variância das semanas das flores por

\[ \hat \sigma^2_2 = \frac{s^2_2}{n_2} \]
Daí, supondo $H_0$, a estimativa da variância populacional é

\[ \hat \sigma^2 = \frac{s^2_1}{n_1} + \frac{s^2_2}{n_2} \]
E o erro-padrão será

\[ EP = \sqrt{\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}} \]

Valores

Tamanhos das amostras: $n_1 = n_2 = 5$.
Médias amostrais: $\bar x_1 = 0{,}417$ e $\bar x_2 = 0{,}151$.
desvios-padrão amostrais: $s_1 = 0{,}1811$ e $s_2 = 0{,}067$.
Hipótese de nulidade: $H_0 : \mu_1 - \mu_2 = 0$.
Hipótese alternativa: $H_A : \mu_1 - \mu_2 \neq 0$.
Nível de significância: $\alpha = 0{,}05$.

Cálculos

n_1 <- length(amostra_1)
xbarra_1 <- mean(amostra_1)
s_1 <- sd(amostra_1)

n_2 <- length(amostra_2)
xbarra_2 <- mean(amostra_2)
s_2 <- sd(amostra_2)

d0 <- 0
dx <- xbarra_1 - xbarra_2
d_cauda_esquerda <- d0 - dx
  
ep <- sqrt(s_1^2 / n_1 + s_2^2 / n_2)
ep

## [1] 0,08635708

A distribuição amostral de $\bar x_1 - \bar x_2$, supondo $H_0$

Como não sabemos o desvio-padrão populacional, precisamos usar a distribuição $t$.

A média da distribuição $t$ é $0$. Precisamos padronizar os valores:

dx

## [1] 0,266

tx <- (dx - d0)/ep
tx

## [1] 3,080234

t_cauda_esquerda <- (d_cauda_esquerda - d0)/ep

Quantos graus de liberdade?

O número de graus de liberdade é dado por

\[ \nu = \frac{ \left( \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} \right)^2 }{ \frac{(s_1^2 / n_1)^2}{n_1 - 1} + \frac{(s_2^2 / n_2)^2}{n_2 - 1} } \]
```
gl <- (s_1^2 / n_1 + s_2^2 / n_2)^2 / (
  (s_1^2 / n_1)^2 / (n_1 - 1) +
  (s_2^2 / n_2)^2 / (n_2 - 1)
)

gl
```
```
## [1] 5,075131
```
Graficamente:

Valor $p$ e conclusão

valor_p <- 
  pt(t_cauda_esquerda, gl) +
  pt(tx, gl, lower.tail = FALSE)

valor_p

## [1] 0,02692873

Este valor é menor do que $\alpha = 0{,}05$. Logo, nossa amostra é evidência para rejeitar a hipótese de nulidade neste nível de significância.

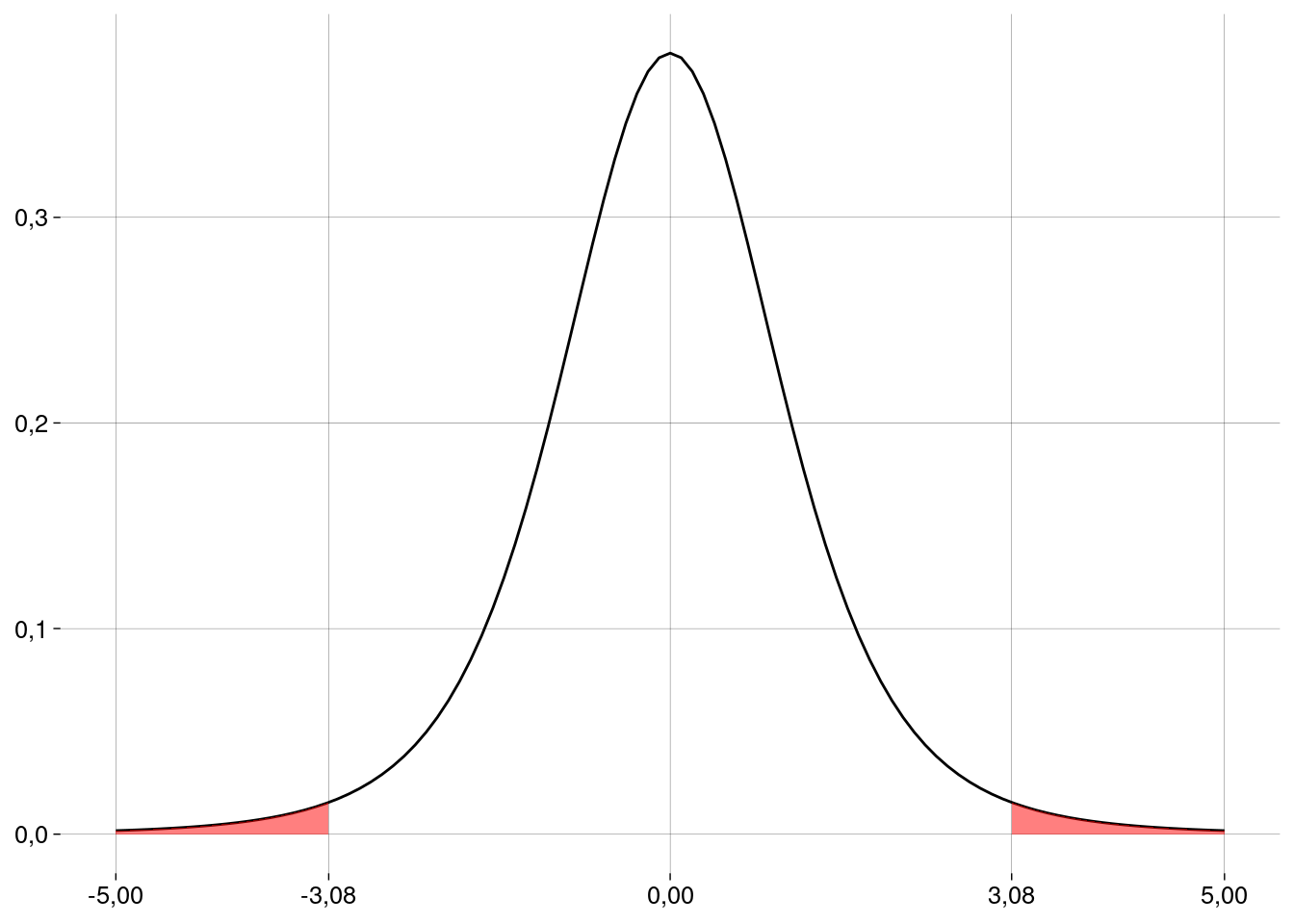
Em R

t.test(amostra_1, amostra_2)

## 
##  Welch Two Sample t-test
## 
## data:  amostra_1 and amostra_2
## t = 3,0802, df = 5,0751, p-value = 0,02693
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  0,04499686 0,48700314
## sample estimates:
## mean of x mean of y 
##     0,417     0,151

E se as arrecadações médias tiverem o mesmo $\sigma$?

O cálculo do erro-padrão muda.
A variância agregada é

\[ s^2 = \frac{(n_1 - 1)s_1^2}{(n_1 + n_2 - 2)} + \frac{(n_2 - 1)s_2^2}{(n_1 + n_2 - 2)} \]

O erro-padrão fica

\[ EP = \sqrt{\frac{s^2}{n_1} + \frac{s^2}{n_2}} \]

onde $s^2$ é a variância agregada, calculada acima.

var_agregada <- (
  (n_1 - 1) * var(amostra_1) + (n_2 - 1) * var(amostra_2)
) / (n_1 + n_2 - 2)

ep <- sqrt(var_agregada / n_1 + var_agregada / n_2)
ep

## [1] 0,08635708

O número de graus de liberdade fica mais simples:
```
gl <- n_1 + n_2 - 2
gl
```
```
## [1] 8
```

Refazendo os cálculos:

tx <- (dx - d0)/ep
tx

## [1] 3,080234

t_cauda_esquerda <- (d_cauda_esquerda - d0)/ep

valor_p <- 
  pt(t_cauda_esquerda, gl) +
  pt(tx, gl, lower.tail = FALSE)

valor_p

## [1] 0,01511156

Supondo o mesmo desvio-padrão para as duas subpopulações, o valor $p$ fica ainda menor. Como o valor é menor do que $\alpha = 0{,}05$, nossa amostra é evidência para rejeitar a hipótese de nulidade neste nível de significância.

Em R:

t.test(amostra_1, amostra_2, var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  amostra_1 and amostra_2
## t = 3,0802, df = 8, p-value = 0,01511
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  0,06686022 0,46513978
## sample estimates:
## mean of x mean of y 
##     0,417     0,151

13.6.3 Diferença entre médias (amostras pareadas)

Exemplo: quilometragem

Durante um ano, um órgão público mediu a quilometragem total de seus $11$ motoristas em um regime de trabalho de $5$ dias por semana.
No ano seguinte, os mesmos $11$ motoristas trabalharam $4$ dias por semana, e as quilometragens totais foram medidas novamente.
Os resultados foram:
A diferença nas quilometragens foi significativa?
Exemplo baseado em https://www.thefreelibrary.com/Four-day+work+week+improves+environment.-a019280161

As amostras agora são pareadas.
O que nos interessa é a diferença na quilometragem de cada motorista.
Vamos fazer um teste $t$ sobre as diferenças (os valores da última coluna).

Condições

Independência entre os pares: o comportamento de cada motorista independe do comportamento dos outros.
Amostras aleatórias e representativas: vamos supor que sim.
Tamanho das amostras: as amostras são menos do que $10\%$ da população.
Dados aproximadamente normais: vejamos um histograma das diferenças:

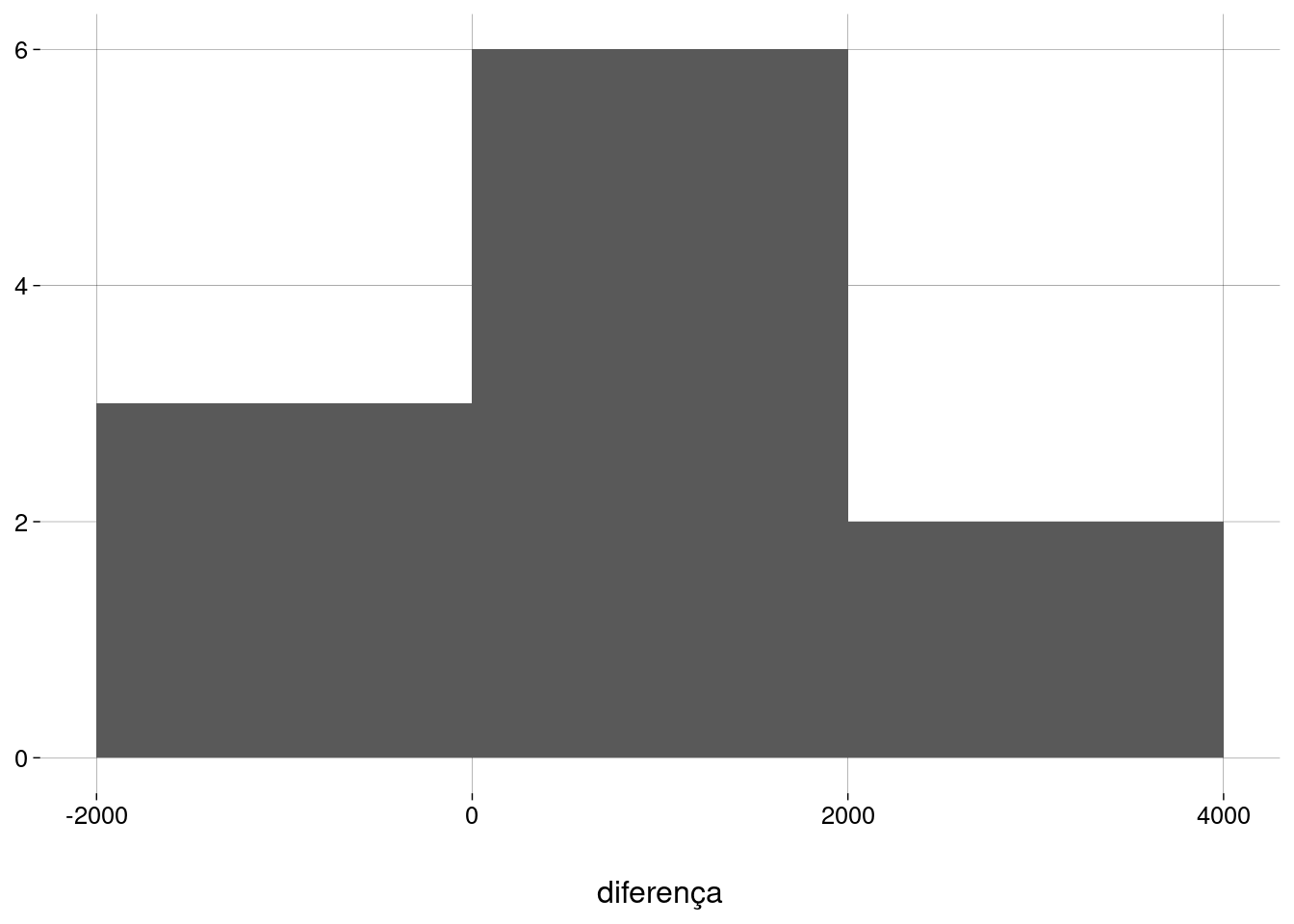
Hipóteses

O teste, agora, é sobre a média das diferenças:

\[ H_0 : \mu_d = 0 \\ H_A : \mu_d \neq 0 \]

Erro padrão

Como o erro-padrão de $\mu$, mas, aqui, $n$ é o número de pares.

\[ EP = \frac{s_d}{\sqrt n} \]

onde $s_d$ é o desvio-padrão das diferenças.

Valores

Tamanho da amostra: $n = 11$.
Média amostral: $\bar d = 982$.
desvio-padrão amostral: $s_d = 1.139{,}57$.
Hipótese de nulidade: $H_0 : \mu_d = 0$.
Hipótese alternativa: $H_A : \mu_d \neq 0$.
Nível de significância: $\alpha = 0{,}05$.

Cálculos

n <- length(df$diferença)
d_barra <- mean(df$diferença)
s_d <- sd(df$diferença)

d0 <- 0
  
ep <- s_d / sqrt(n)
ep

## [1] 343,5928

A distribuição amostral de $\bar d$

Como não sabemos o desvio-padrão populacional, precisamos usar a distribuição $t$.

A média da distribuição $t$ é $0$. Precisamos padronizar os valores:

d_barra

## [1] 982

t_barra <- (d_barra - d0)/ep
t_barra

## [1] 2,858034

O número de graus de liberdade é $n - 1 = 10$.
```
gl <- n - 1
```
Graficamente:

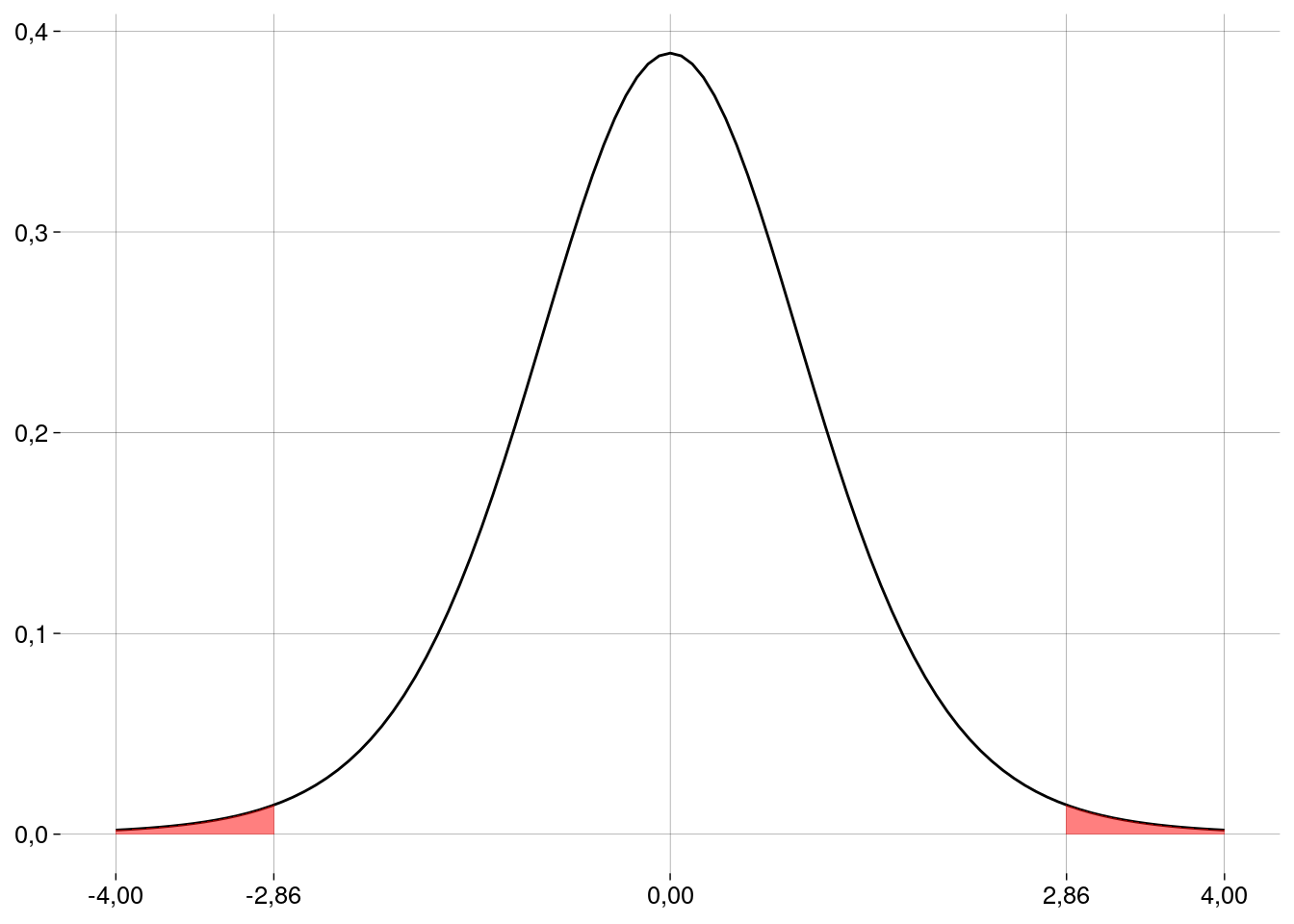
Valor $p$ e conclusão

valor_p <- 2 * pt(t_barra, gl, lower.tail = FALSE)
valor_p

## [1] 0,01701413

Este valor é menor do que $\alpha = 0{,}05$, nossa amostra é evidência para rejeitar a hipótese de nulidade neste nível de significância. A quilometragem média variou de um ano para o outro.

Em R

t.test(
  df$dias_5, 
  df$dias_4,
  paired = TRUE
)

## 
##  Paired t-test
## 
## data:  df$dias_5 and df$dias_4
## t = 2,858, df = 10, p-value = 0,01701
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##   216,4276 1747,5724
## sample estimates:
## mean difference 
##             982

13.7 Outros testes em R

Diversas outras funções em R apresentam os resultados de testes em termos de intervalos de confiança e/ou valores $p$.

13.7.1 Teste de normalidade de Shapiro-Wilk

A hipótese de nulidade é $H_0: {}$ a amostra vem de uma distribuição normal.

Então, um valor $p$ alto é evidência a favor da normalidade dos dados:

x <- rnorm(100, 5, 3)
shapiro.test(x)

## 
##  Shapiro-Wilk normality test
## 
## data:  x
## W = 0,99388, p-value = 0,9349

x <- runif(100, 0, 1)
shapiro.test(x)

## 
##  Shapiro-Wilk normality test
## 
## data:  x
## W = 0,9454, p-value = 0,0004182

13.7.2 Teste para comparar variâncias

A hipótese de nulidade é $H_0 : \sigma^2_x / \sigma^2_y = r$, onde o valor default de $r$ é $1$.

Testando as amostras do experimento olhos $\times$ flores:

var.test(amostra_1, amostra_2)

## 
##  F test to compare two variances
## 
## data:  amostra_1 and amostra_2
## F = 7,304, num df = 4, denom df = 4, p-value = 0,08003
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##   0,7604789 70,1518943
## sample estimates:
## ratio of variances 
##           7,304042

13.7.3 Teste de correlação

A hipótese de nulidade é $H_0 : {}$ as variáveis (pareadas) $x$ e $y$ não são correlacionadas.

Testando as amostras do exemplo dos motoristas:

cor.test(df$dias_4, df$dias_5)

## 
##  Pearson's product-moment correlation
## 
## data:  df$dias_4 and df$dias_5
## t = 13,671, df = 9, p-value = 0,0000002518
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0,9101992 0,9941362
## sample estimates:
##       cor 
## 0,9767585

12 Intervalos de confiança

14 Covariância e correlação

Capítulo 13 Testes de hipóteses

13.1 Vídeo 1

13.2 Testes de hipóteses sobre a proporção

13.2.1 Exemplo: proporção de bebês do sexo masculino

Hipóteses

Condições

Valores

Estratégia

A distribuição amostral de \(\hat p\), supondo \(H_0\)

O valor \(p\) e a conclusão

Em R

13.2.2 Exemplo: percepção extra-sensorial

Hipóteses

Condições

Valores

Estratégia

A distribuição amostral de \(\hat p\), supondo \(H_0\)

O valor \(p\) e a conclusão

Em R

13.2.3 Erros, poder e tamanho do efeito

Rejeitar \(\times\) não rejeitar

Erro tipo 1: rejeitar quando não devíamos

Erro tipo 2: não rejeitar quando devíamos

Poder de um teste

O tamanho do efeito

Explorando tudo interativamente

13.2.4 Exercícios

Usando binom.test

Outro suposto vidente

13.3 Vídeo 2

13.4 Testes de hipóteses sobre a média

13.4.1 Exemplo: duração da gestação

Hipóteses

Condições

Valores

O valor \(p\) e a conclusão

Em R

13.4.2 Exemplo: salmões novamente

Hipóteses

Condições

Valores

O valor \(p\) e a conclusão

Em R

13.4.3 Relação entre testes e IC

13.4.4 Explorando tudo interativamente (com outro app)

13.4.5 Exercícios

Gestação

Salmões

Testes e IC

App

13.5 Vídeo 3

13.6 Testes de hipóteses com duas amostras

13.6.1 Diferença entre proporções

Exemplo: jovens online

Condições

Hipóteses

Erro padrão

Valores

Cálculos

A distribuição amostral de \(\hat p_h - \hat p_m\), supondo \(H_0\)

Valor \(p\) e conclusão

Em R

13.6.2 Diferença entre médias (amostras independentes)

Exemplo: olhos \(\times\) flores

Amostras

Condições

Hipóteses

Erro padrão (variâncias diferentes)

Valores

Cálculos

A distribuição amostral de \(\bar x_1 - \bar x_2\), supondo \(H_0\)

Valor \(p\) e conclusão

Em R

E se as arrecadações médias tiverem o mesmo \(\sigma\)?

13.6.3 Diferença entre médias (amostras pareadas)

Exemplo: quilometragem

Condições

Hipóteses

Erro padrão

Valores

Usando `binom.test`