Capítulo 7 Probabilidades

7.1 Vídeo 1

7.2 Espaço amostral

• Para falar em probabilidades, precisamos falar de experimentos, resultados, espaços amostrais, e eventos.

• Um experimento probabilístico é um experimento cujo resultado exato é desconhecido a priori; mais ainda: executar o experimento diversas vezes, nas mesmas condições, pode produzir resultados diferentes.

• O espaço amostral é o conjunto de todos os resultados possíveis de um experimento probabilístico, representados de alguma forma.

• Exemplos:

  1. Experimento: lançar uma moeda;
     Espaço amostral: $\{ K, C \}$ (onde $K$ é cara, $C$ é coroa).

  2. Experimento: lançar $2$ moedas;
     Espaço amostral: $\{ (K,K), (K,C), (C,K), (C,C) \}$.

  3. Experimento: lançar um dado;
     Espaço amostral: $\{ 1, 2, 3, 4, 5, 6 \}$.

  4. Experimento: lançar $2$ dados:
     Espaço amostral: $\{ (1, 1), (1, 2), \ldots, (6, 5), (6, 6) \}$.

7.3 Evento

• Um evento é um subconjunto do espaço amostral; ou seja, um evento é um conjunto de resultados.

• Exemplos:

  1. Lançar uma moeda e obter cara:
     $\{ K \}$.

  2. Lançar 2 moedas e obter resultados iguais:
     $\{ (K,K), (C,C) \}$.

  3. Lançar um dado e obter um número maior que 4:
     $\{ 5, 6 \}$.

  4. Lançar 2 dados e obter 2 números iguais:
     $\{ (1,1), (2,2), (3,3), (4,4), (5,5), (6,6) \}$.

• Dizemos que o evento $A$ ocorreu se o experimento foi realizado e o resultado obtido está no conjunto que corresponde ao evento $A$.

7.4 Análise Combinatória

• Para calcularmos probabilidades, vamos precisar contar a quantidade de certos objetos complexos (formados por partes menores).

• Existem técnicas de contagem, que são assunto de Análise Combinatória.

• Exemplos:

  1. Quantas senhas de $6$ caracteres (dentre letras e dígitos apenas) existem, sem distinguir entre minúsculas e maiúsculas?

     • O conjunto de letras e dígitos tem $36$ elementos.

     • A resposta é $36^{6} = 2.176.782.336$.

  2. E se não puder haver repetição de caracteres?

     • Agora, a resposta é $$36 \cdot 35 \cdot 34 \cdot 33 \cdot 32 \cdot 31 = 1.402.410.240$$

• Se você nunca tiver estudado técnicas de contagem, ou se quiser revisar ou aprender mais, consulte o excelente livro Morgado et al. (2004).

7.5 Probabilidade clássica

• Nesta abordagem simples — que pode não ser a correta para o problema que estamos tentando resolver —, cada resultado do espaço amostral tem a mesma chance de ocorrer.

• Ou seja, para um evento $A$, a probabilidade $P(A)$ é

  $$P(A) = \frac{\text{Qtde de resultados em } A}{\text{Qtde de resultados no espaço amostral}}$$

• Exemplo: de um baralho normal, de $52$ cartas, qual a probabilidade de escolher uma carta ao acaso e obter

  1. Uma carta de ouros?

     $$\frac{13}{52} = \frac{1}{4}$$

  2. Uma carta vermelha?

     $$\frac{26}{52} = \frac{1}{2}$$

  3. Uma carta de figura (J, Q ou K)?

     $$\frac{12}{52} = \frac{3}{13}$$

  4. Uma carta de ouros, copas, paus ou espadas?

     $$\frac{52}{52} = 1$$

  5. Um carta de um naipe verde?

     $$\frac{0}{52} = 0$$

  Só podemos usar este raciocínio se todos os resultados do experimento tiverem a mesma probabilidade de ocorrer.

  Como a carta é escolhida ao acaso, esta condição é satisfeita neste exemplo.

7.6 Probabilidade empírica

• Baseada em repetições de um experimento probabilístico.

• Nesta abordagem, a probabilidade de um evento é sua frequência relativa:

  $$P(A) = \frac{\text{Qtde de ocorrências de } A}{\text{Qtde total de repetições do experimento}}$$

• Esta abordagem é fácil de usar quando é possível repetir o experimento muitas vezes, nas mesmas condições (lançar uma moeda, escolher uma carta de um baralho).

• Em outros casos (calcular a probabilidade de um candidato vencer uma eleição), não é possível repetir o experimento nas mesmas condições.

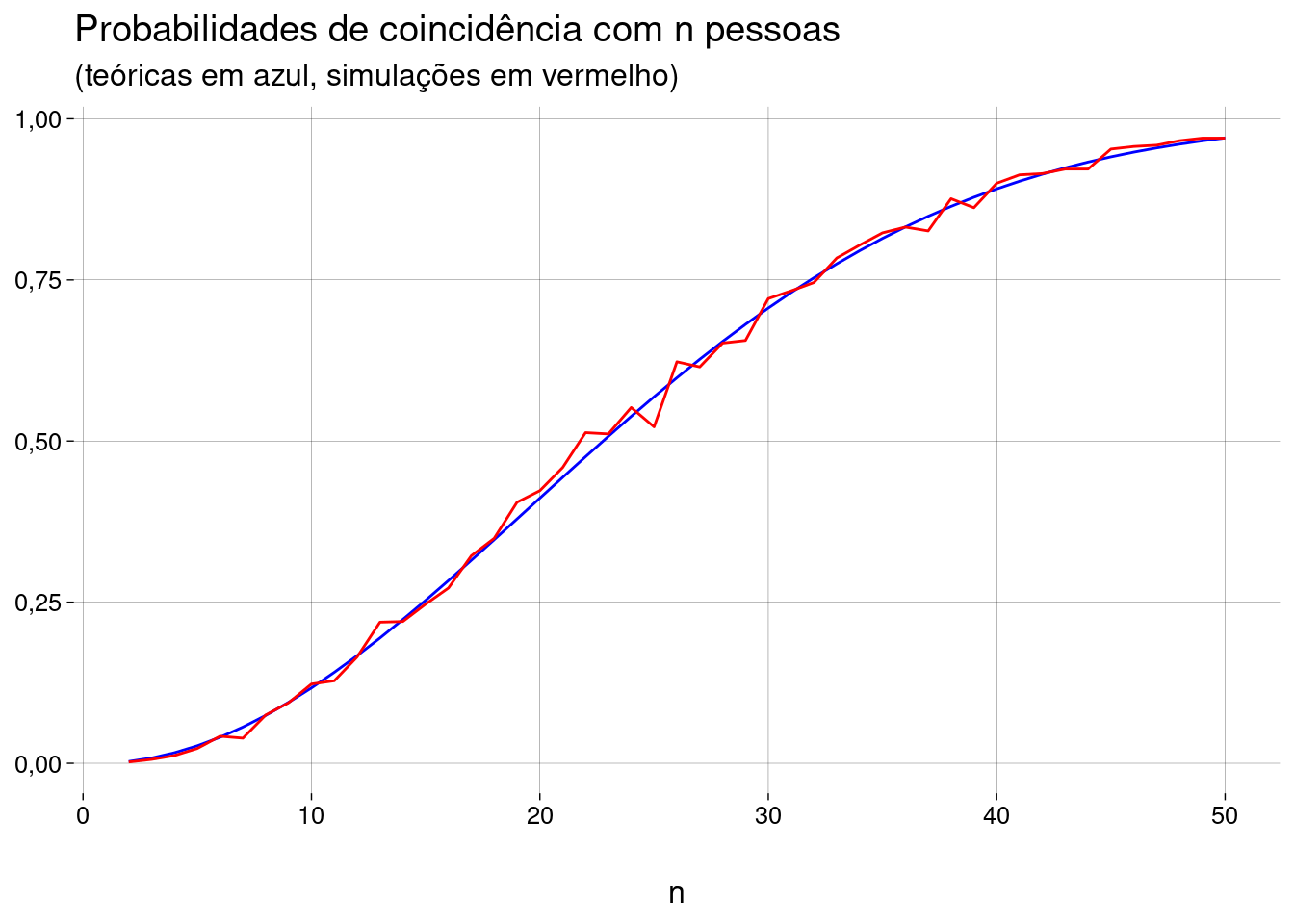
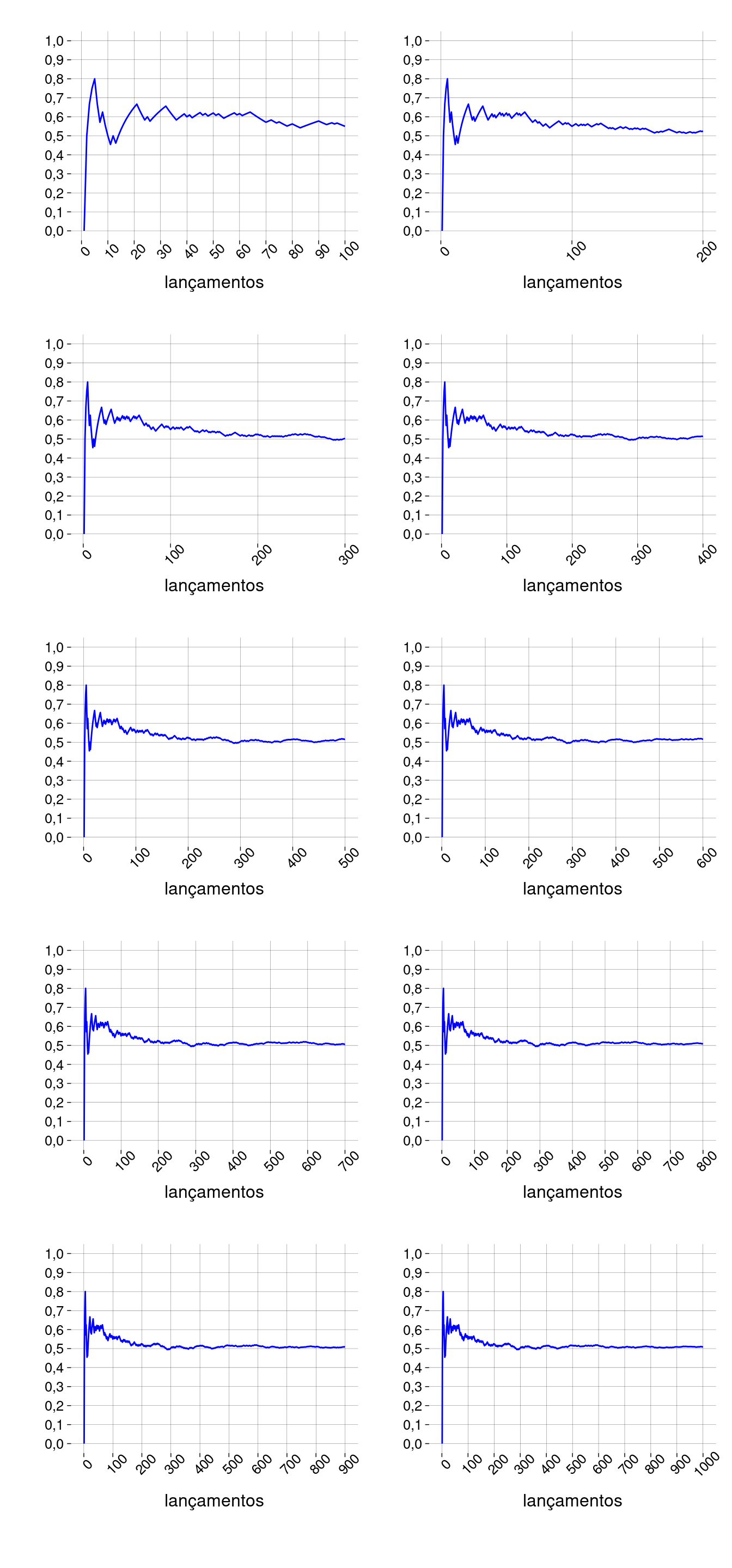
• Exemplo: se lançarmos uma moeda não-viciada muitas vezes, a proporção de caras vai ser aproximadamente $0{,}5$. Os gráficos abaixo mostram como, à medida que o número de lançamentos aumenta (no eixo horizontal), a proporção de caras (no eixo vertical) vai se aproximando de $0{,}5$:

  

• A lei dos grandes números é um resultado matemático que diz, essencialmente, que, quando o número $n$ de repetições de um experimento tende a infinito, a frequência relativa de um evento tende à sua probabilidade real.

  A falácia do jogador

  Um erro comum é achar que, se houve poucas caras nos lançamentos mais recentes, então a probabilidade de o resultado ser cara no próximo lançamento é maior, para que a proporção de caras fique mais perto de $0{,}5$.

  A lei dos grandes números fala sobre os resultados do experimento quando $n$ tende ao infinito, não no futuro próximo.

  Em lançamentos independentes de uma moeda não-viciada, a probabilidade de cara sempre é $0{,}5$.

7.7 Probabilidade subjetiva

• Outra interpretação de probabilidades se baseia na crença — a estimativa de um agente sobre a ocorrência de um evento.

• Uma maneira de quantificar a crença é através de apostas justas.

• Por exemplo, você aposta com um amigo que

  • Se o seu time de basquete⁸ vencer o próximo jogo contra o dele, ele pagará $\$3$ para você.

  • Se o time dele vencer o próximo jogo contra o seu, você pagará $\$1$ para ele.

• Se você considera justa esta aposta, então você crê que a probabilidade de o time dele vencer é $3$ vezes maior do que a probabilidade de o seu time vencer.

• Como a soma das probabilidades de um evento e do evento complementar deve ser $1$, isto equivale a dizer que

  $$P(\text{seu time vencer}) = 1/4 \qquad\text{e}\qquad P(\text{time dele vencer}) = 3/4$$

• Em mais detalhes:

  • Você pode receber menos com uma probabilidade maior,

  • Seu amigo pode receber mais com uma probabilidade menor,

  • A razão entre as quantias ($3$) é contrabalançada exatamente pela razão entre as probabilidades ($1/3$).

7.8 Formalização de probabilidades

• Para trabalhar matematicamente com probabilidades, é preciso definir as “regras do jogo”.

• Tudo que se pode concluir sobre probabilidades é consequência dos seguintes axiomas, formulados por Kolmogorov em 1933:

  1. $0 \leq P(A) \leq 1$, para qualquer evento $A$.

  2. $P(\Omega) = 1$, onde $\Omega$ é o espaço amostral (o conjunto de todos os resultados possíveis do experimento em questão);

  3. $P(\bar A) = 1 - P(A)$, onde $\bar A$ é o evento complementar de $A$ (i.e., o evento que corresponde a $A$ não ocorrer)

  4. $P(A_1 \cup \cdots \cup A_n) = P(A_1) + \cdots + P(A_n)$, onde $A_1, \ldots, A_n$ são eventos disjuntos dois a dois (i.e., $A_i$ e $A_j$ não podem ocorrer ao mesmo tempo, para todo par $(i, j)$ com $i \neq j$).

• Mostre, a partir dos axiomas acima, que

  $$P(\varnothing) = 0$$

  $$\varnothing = \bar \Omega$$

  $$\begin{aligned} P(\varnothing) &= P(\bar \Omega) \\ &= 1 - P(\Omega) & \text{(pelo axioma 3)}\\ &= 1 - 1 & \text{(pelo axioma 2)} \\ &= 0 \end{aligned}$$

7.9 Eventos independentes (explicação informal)

• Se a ocorrência de $A$ não influencia a ocorrência de $B$, nem vice-versa, dizemos que os eventos $A$ e $B$ são independentes.

• Exemplo:

  • O experimento é lançar um dado duas vezes.

  • $A$ é o evento o primeiro lançamento deu um número par.

  • $B$ é o evento o segundo lançamento deu 6.

  • Saber se $A$ aconteceu não nos ajuda em nada a estimar se $B$ aconteceu.

  • Aqui, $A$ e $B$ são independentes.

• Outro exemplo:

  • O experimento é lançar um dado duas vezes.

  • $A$ é o evento o primeiro lançamento deu um número menor que $3$.

  • $B$ é o evento a soma dos dois lançamentos é maior que $8$.

  • Agora, saber se $A$ aconteceu ajuda a estimar se $B$ aconteceu.

  • Na verdade, se $A$ aconteceu, $B$ é impossível (a probabilidade de $B$, dado $A$, é $0$).

  • Se $A$ não aconteceu, a probabilidade de $B$ é $5/12$.

  • Aqui, $A$ e $B$ não são independentes.

• A probabilidade de os eventos $A$ e $B$ acontecerem ao mesmo tempo é escrita como

  $$P(A, B) \qquad \text{ou como} \qquad P(A \cap B)$$

• Quando $A$ e $B$ são independentes,

  $$P(A, B) = P(A) \cdot P(B)$$

• Ou seja, quando $A$ e $B$ são independentes, a probabilidade de $A$ e $B$ acontecerem ao mesmo tempo é igual ao produto das probabilidades de $A$ e de $B$.

• Mais adiante, vamos ver uma definição formal de independência, e vamos provar esta última igualdade.

7.10 $P(A \cup B)$ com $A$ e $B$ não-disjuntos

• Um dos axiomas de probabilidade fala sobre a probabilidade da união de vários eventos disjuntos (sem elementos em comum):

  $$P(A_1 \cup \cdots \cup A_n) = P(A_1) + \cdots + P(A_n)$$

• E se os eventos não forem disjuntos?

• Veja a figura abaixo:

  

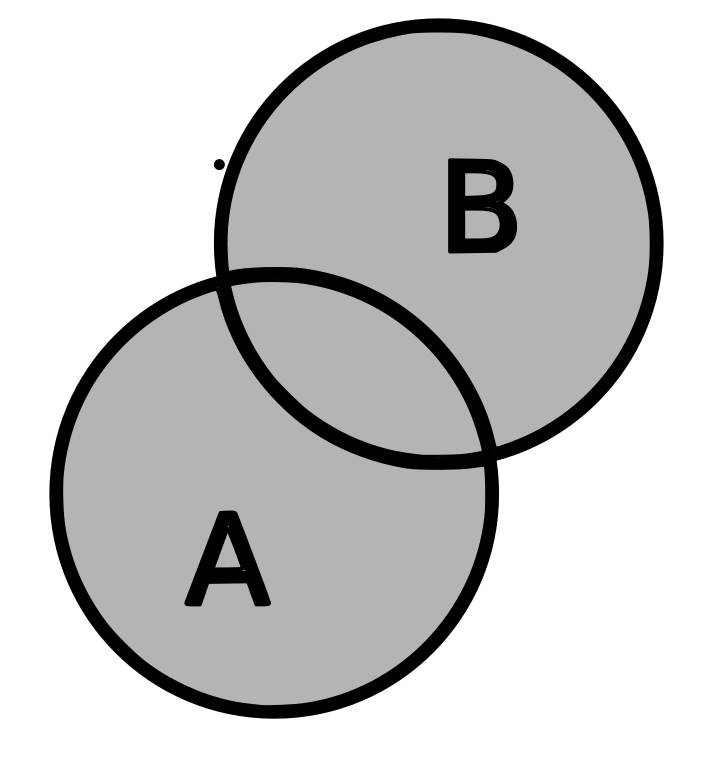
• Imagine que a probabilidade de um evento é proporcional à sua área nesta figura.

• Se você somar a área de $A$ com a área de $B$, você vai estar contando duas vezes a área comum aos dois (a área que corresponde a $A \cap B$).

• Por isso, o certo é “descontar” esta área.

• O resultado é

  $$P(A \cup B) = P(A) + P(B) - P(A \cap B)$$

• Exemplo: suponha que 25% das pessoas têm cachorro, 29% das pessoas têm gato, e 12% das pessoas têm cachorro e gato.

• Qual a probabilidade de que uma pessoa tenha gato ou cachorro ou ambos?

  $$\begin{aligned} P(\text{cachorro } \cup \text{ gato}) &= P(\text{cachorro}) + P(\text{gato}) - P(\text{cachorro } \cap \text{ gato}) \\ &= 0{,}25 + 0{,}29 - 0{,}12 \\ &= 0{,}42 \end{aligned}$$

• No geral, para $n$ eventos $A_1, \ldots, A_n$:

  $$\begin{aligned} P(A_1 \cup \cdots \cup A_n) &= P(A_1) + \cdots + P(A_n) \\ & - P(A_1 \cap A_2) - \cdots - P(A_{n-1} \cap A_n) \\ & + P(A_1 \cap A_2 \cap A_3) + \cdots + P(A_{n-2} \cap A_{n-1} \cap A_n) \\ & \cdots \\ & \pm P(A_1 \cap \cdots \cap A_n ) \end{aligned}$$

• Na última linha

  • o sinal vai ser $+$ se $n$ for ímpar;

  • o sinal vai ser $-$ se $n$ for par;

  • poderíamos escrever, então, $(-1)^{n+1} \cdot P(A_1 \cap \cdots \cap A_n )$.

• Escreva, seguindo o padrão acima, a expressão para

  $$P(A \cup B \cup C)$$

  $$\begin{aligned} P(A \cup B \cup C) &= P(A) + P(B) + P(C) \\ & - P(A \cap B) - P(A \cap C) - P(B \cap C) \\ & + P(A \cap B \cap C) \end{aligned}$$

7.11 Problema do aniversário

7.11.1 Solução teórica

• Em uma sala estão $25$ pessoas escolhidas ao acaso.

• Qual a probabilidade de que pelo menos $2$ delas façam aniversário no mesmo dia do ano?

• Premissas:

  • Os dias dos aniversários das pessoas são independentes.

  • Cada dia do ano tem a mesma probabilidade de ser o aniversário de alguém.

  • Vamos ignorar anos bissextos. Cada ano tem 365 dias.

• Queremos achar $P(I)$, onde $I$ é o evento de que pelo menos duas pessoas têm aniversários iguais.

• Vamos calcular a probabilidade $P(N)$ de que não haja aniversários iguais.

• Este evento $N$ é o complementar do evento $I$, i.e., $N = \bar I$.

• Então, $P(I) = 1 - P(N)$.

• $P(N)$ é a probabilidade de que todos os aniversários caiam em dias diferentes:

  • A pessoa $1$ pode ter nascido em qualquer dia do ano.

  • A pessoa $2$ precisa ter nascido em algum dos outros $364$ dias. A probabilidade é $\frac{364}{365}$.

  • A pessoa $3$ precisa ter nascido em algum dos outros $363$ dias. A probabilidade é $\frac{363}{365}$.

  • $\ldots$

  • A pessoa $25$ precisa ter nascido em algum dos outros $341$ dias. A probabilidade é $\frac{341}{365}$.

• Como os nascimentos são independentes, a probabilidade de todos os eventos acontecerem juntos é o produto das probabilidades:

  $$P(N) = \frac{364}{365} \cdot \frac{363}{365} \cdot \cdots \cdot \frac{341}{365} = \frac{364 \cdot 363 \cdot \cdots \cdot 341}{365^{24}}$$

• O que dá

  pn <- prod((364:341)/365)
  pn

  ## [1] 0,4313003

• Então, $P(I)$ é

  1 - pn

  ## [1] 0,5686997

• Surpreso? Com $25$ pessoas na sala, é mais provável haver do que não haver coincidência de aniversários!

7.11.2 Simulação

• Vamos simular milhares de salas com $25$ pessoas satisfazendo as premissas e ver em quantas delas há coincidência de aniversários. Examine o código abaixo:

  nsalas <- 1e4
  npessoas <- 25
  
  coincidencia <- function(sala) {
  
    # Se a quantidade de valores únicos for diferente 
    # da quantidade total de valores, então há repetição  
    !(length(unique(sala)) == length(sala))
  
  }
  
  gerar_e_testar <- function(npessoas) {
  
    # Escolhemos, ao acaso, npessoas números entre 1 e 365,
    # com reposição
    sala <- sample(1:365, npessoas, replace = TRUE)
  
    # Testamos se há alguma coincidência de aniversários
    coincidencia(sala)
  
  }
  
  simular <- function(npessoas, nsalas) {
  
    resultados <- replicate(nsalas, gerar_e_testar(npessoas))
  
    # Como resultados é um vetor booleano, tirar a média
    # vai dar a proporção de resultados verdadeiros,
    # que é a probabilidade.
    mean(resultados)
  
  }
  
  simular(npessoas, nsalas)

  ## [1] 0,5712

7.11.3 Para diferentes valores de $n \in \{2, 3, \ldots, 50\}$

Soluções teóricas

• Vamos calcular as probabilidades de coincidência para diferentes quantidades $n$ de pessoas na sala e fazer um gráfico:

  npessoas <- 2:50
  
  p <- function(n) {
  
    # Fórmula geral, para n pessoas
    1 - prod((364:(366 - n))/365)
  
  }
  
  probs <- sapply(npessoas, p)
  
  grafico <- probs %>% 
    as_tibble() %>% 
    ggplot(aes(x = npessoas, y = value)) +
      geom_line(color = 'blue') +
      labs(
        title = 'Probabilidades de coincidência com n pessoas',
        y = NULL,
        x = 'n'
      )
  
  grafico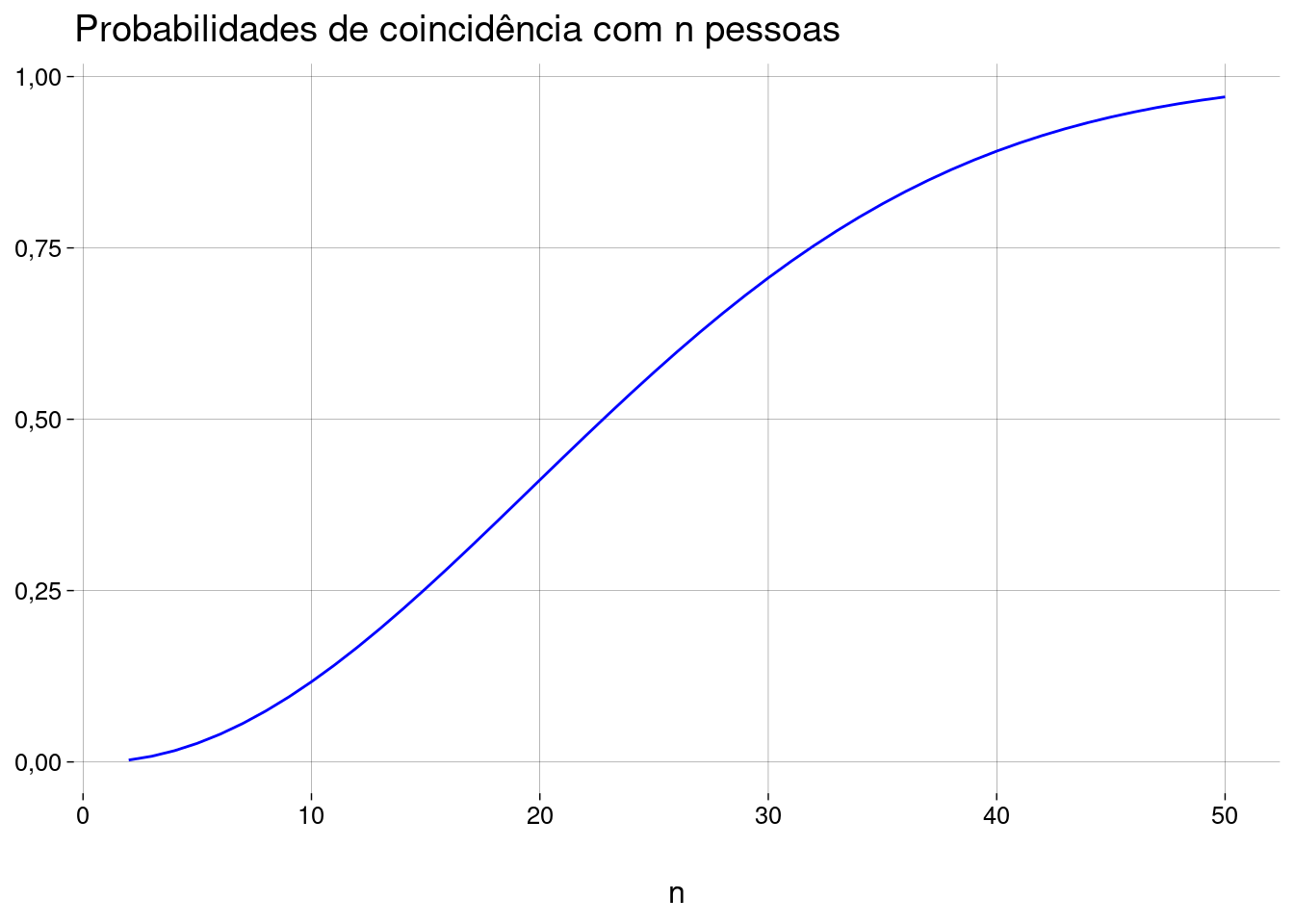

  

• Este problema é tão usado em cursos de probabilidade que o R oferece as funções pbirthday e qbirthday.

• Leia a ajuda de pbirthday e recrie o gráfico acima usando esta função.

• Leia a ajuda de qbirthday e responda:

  • Quantas pessoas são necessárias para que a probabilidade de uma ou mais coincidências seja de pelo menos $50\%$?

    Os valores default dos argumentos resolvem este problema:

    qbirthday()

    ## [1] 23

  • Quantas pessoas são necessárias para que a probabilidade de uma ou mais coincidências seja de pelo menos $90\%$?

    qbirthday(.9)

    ## [1] 41

  • Quantas pessoas são necessárias para que haja uma probabilidade de pelo menos $50\%$ de que $5$ ou mais pessoas façam aniversário no mesmo dia?

    qbirthday(coincident = 5)

    ## [1] 313

Simulação

nsalas <- 1e3
npessoas <- 2:50

probs_sim <- sapply(npessoas, simular, nsalas)

grafico +
  geom_line(
    data = as_tibble(probs_sim),
    mapping = aes(y = value),
    color = 'red'
  ) +
  labs(
    subtitle = '(teóricas em azul, simulações em vermelho)'
  )

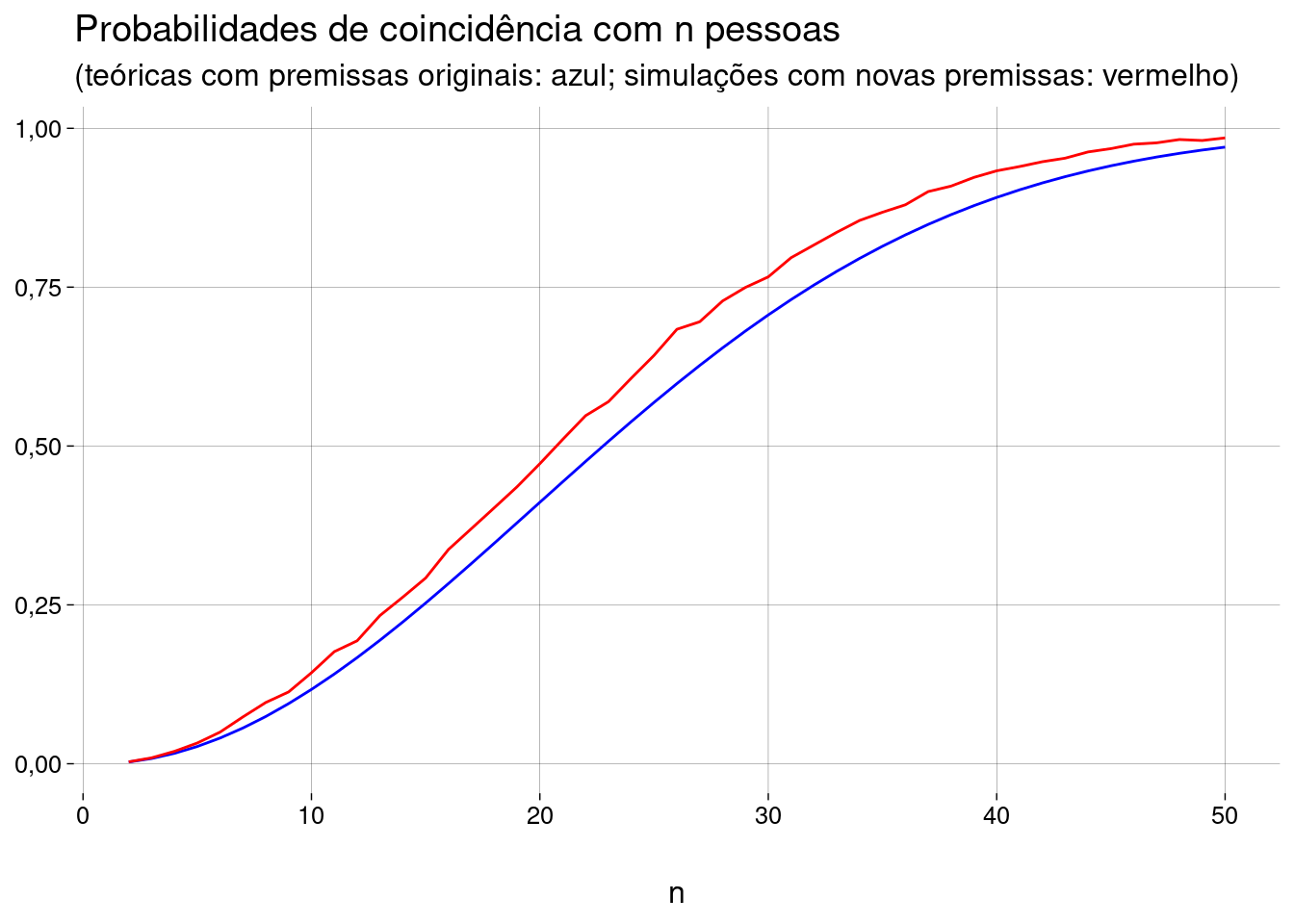
7.11.4 Premissas mais realistas

• Vamos considerar anos bissextos. O total de dias muda para $366$, mas um dos dias ($29$ de fevereiro) tem $1/4$ da probabilidade de um dia normal de ser o aniversário de alguém.

• Além disso, vamos supor que haja $165$ dias em que a probabilidade de alguém nascer é $25\%$ maior do que nos $200$ dias normais.

• A solução teórica é bem mais complexa do que no caso uniforme!

• Vamos fazer apenas a simulação.

• Preste atenção no vetor pesos, que representam as probabilidades de dias diferentes:

  • $200$ dias normais têm peso $4$;

  • $165$ dias mais prováveis têm peso $5$;

  • $1$ dia ($29$ de fevereiro) tem peso $1$.

• Estes pesos não são probabilidades, porque a soma deles não é $1$.

• A função sample normaliza automaticamente estes pesos.

• Normalizar significa dividir todos os valores pela mesma constante, de forma que a soma seja $1$.

  nsalas <- 1e3
  npessoas <- 2:50
  
  pesos <- c(
    rep(4, 200),    # dias normais
    rep(5, 165),    # dias mais prováveis
    1               # 29 de fevereiro
  )
  
  gerar_e_testar <- function(npessoas, pesos) {
  
    sala <- sample(1:366, npessoas, replace = TRUE, prob = pesos)
    coincidencia(sala)
  
  }
  
  simular <- function(npessoas, nsalas, pesos) {
  
    resultados <- replicate(nsalas, gerar_e_testar(npessoas, pesos))
    mean(resultados)
  
  }
  
  novas_probs <- sapply(npessoas, simular, nsalas, pesos)
  
  grafico +
    geom_line(
      data = as_tibble(novas_probs),
      mapping = aes(y = value),
      color = 'red'
    ) +
    labs(
      subtitle = paste(
        '(teóricas, premissas originais: azul;', 
        'simulações, novas premissas: vermelho)'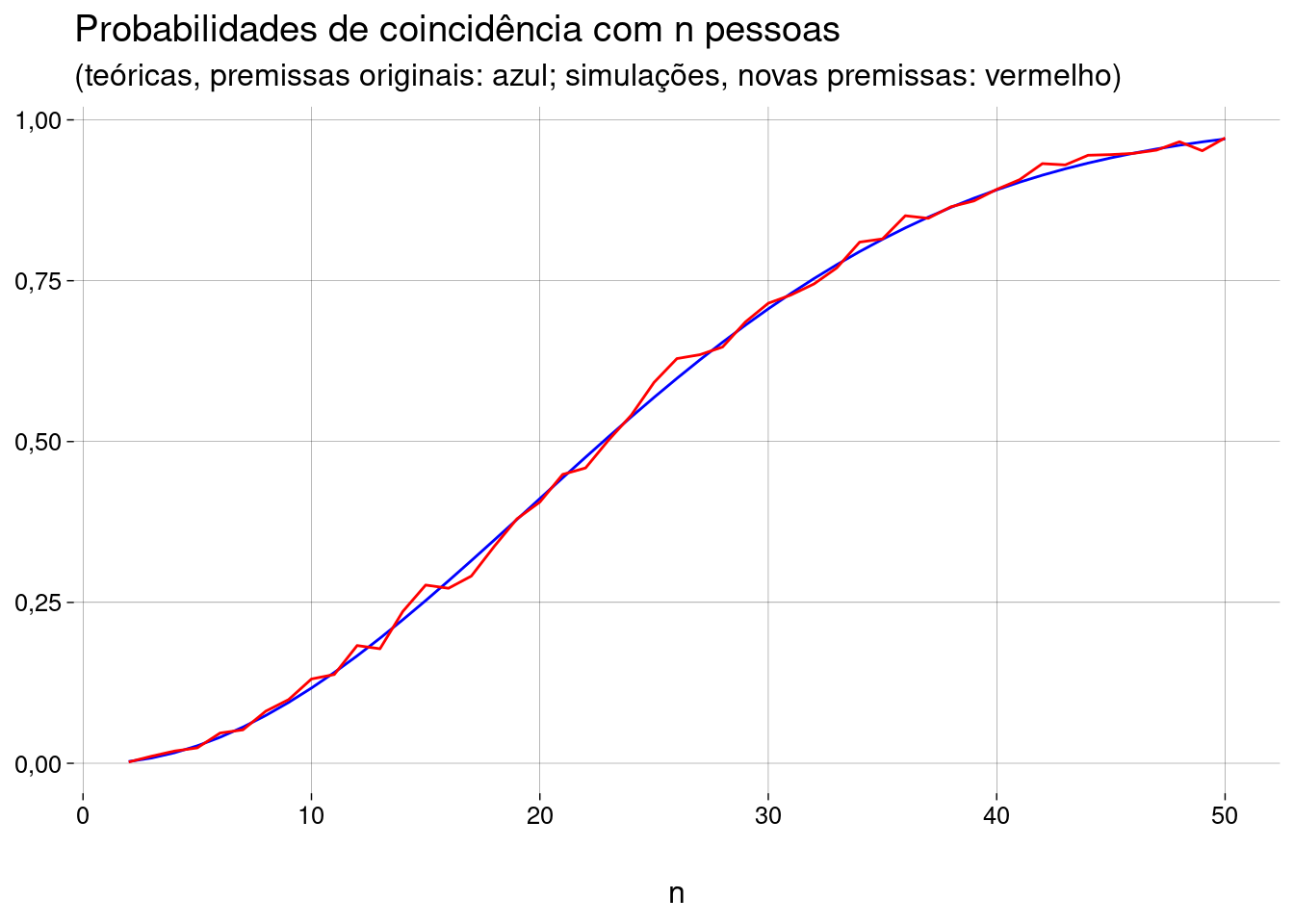
      )
    )

  

• As novas premissas não mudaram muita coisa.

• Escreva a versão normalizada do vetor pesos.

  O vetor original é

  $$( \underbrace{4, \ldots, 4}_{200\text{ vezes}},\;\; \underbrace{5, \ldots, 5}_{165\text{ vezes}},\;\; 1 )$$

  A soma de todos os elementos é

  $$200 \cdot 4 + 165 \cdot 165 + 1 = 1.626$$

  O vetor normalizado fica

  $$\left( \underbrace{\frac4{1626}, \ldots, \frac4{1626}}_{200\text{ vezes}},\;\; \underbrace{\frac5{1626}, \ldots, \frac5{1626}}_{165\text{ vezes}},\;\; \frac1{1626} \right)$$

  ou

  $$\left( \underbrace{\frac2{813}, \ldots, \frac2{813}}_{200\text{ vezes}},\;\; \underbrace{\frac5{1626}, \ldots, \frac5{1626}}_{165\text{ vezes}},\;\; \frac1{1626} \right)$$

7.12 Exercícios

7.12.1 Semanas com mais nascimentos

• Imagine que $50\%$ dos nascimentos de um ano aconteçam em um período de $15$ semanas, e o restante dos nascimentos seja distribuído de maneira uniforme no restante do ano. Ignore anos bissextos.

• Faça simulações como na seção anterior ($2 \leq n \leq 50$) e construa o gráfico comparando com as probabilidades teóricas (com as premissas originais).

• Interprete o resultado.

  • $15$ semanas são $105$ dias.

  • O restante do ano tem $260$ dias.

    nsalas <- 1e4
    npessoas <- 2:50
    
    # Probabilidades teóricas, premissas originais
    p <- function(n) {
    
      1 - prod((364:(366 - n))/365)
    
    }
    
    probs <- sapply(npessoas, p)
    
    grafico <- probs %>% 
      as_tibble() %>% 
      ggplot(aes(x = npessoas, y = value)) +
        geom_line(color = 'blue') +
        labs(
          title = 'Probabilidades de coincidência com n pessoas',
          y = NULL,
          x = 'n'
        )
    
    # Probabilidades com 15 semanas com 50% dos nascimentos
    pesos <- c(
      rep(50/105, 105),    # dias das semanas com mais nascimentos
      rep(50/260, 260)     # dias das semanas normais
    )
    
    coincidencia <- function(sala) {
    
      !(length(unique(sala)) == length(sala))
    
    }
    
    gerar_e_testar <- function(npessoas, pesos) {
    
      sala <- sample(1:365, npessoas, replace = TRUE, prob = pesos)
      coincidencia(sala)
    
    }
    
    simular <- function(npessoas, nsalas, pesos) {
    
      resultados <- replicate(nsalas, gerar_e_testar(npessoas, pesos))
      mean(resultados)
    
    }
    
    novas_probs <- sapply(npessoas, simular, nsalas, pesos)
    
    grafico +
      geom_line(
        data = as_tibble(novas_probs),
        mapping = aes(y = value),
        color = 'red'
      ) +
      labs(
        subtitle = paste(
          '(teóricas com premissas originais: azul;', 
          'simulações com novas premissas: vermelho)'
        )
      )

    

  • Com as novas premissas, a probabilidade de coincidência é maior para quase todos os valores de $n$: a linha vermelha está acima da linha azul.

  • Como metade dos nascimentos está concentrada nas $15$ semanas, a probabilidade de haver coincidência para $n$ pessoas é maior do que com as premissas originais.

7.12.2 Pôquer

• Uma mão de pôquer consiste de $5$ cartas retiradas ao acaso de um baralho de $32$ cartas ($4$ naipes, cada um com cartas 7, 8, 9, 10, J, Q, K, A).

• Calcule as seguintes probabilidades teoricamente e através de simulações.

  1. Qual a probabilidade de obter uma mão sem ases?

     • A ordem das cartas não importa.

     • Basta calcular o número de mãos possíveis usando as $28$ cartas que não são ases:

       $${28 \choose 5} = 98.280$$

     • E dividir pelo total de mão possíveis:

       $${32 \choose 5} = 201.376$$

     • O resultado é aproximadamente $0{,}49$.

     • Criando as cartas:

       baralho <- expand_grid(
         numero = c(7:10, 'J', 'Q', 'K', 'A'),
         naipe = c('♥', '♦', '♣', '♠')
       ) %>% 
         mutate(carta = paste(numero, naipe)) %>% 
         pull(carta)

     • Função para gerar uma mão:

       mao <- function(){
         sample(baralho, size = 5)
       }

     • Testar se a mão tem (pelo menos) um ás:

       tem_as <- function(mao) {
       
         any(str_starts(mao, 'A'))
       
       }

     • Simulação:

       nsim <- 1e6
       maos <- rerun(nsim, mao())

       ## Warning: `rerun()` was deprecated in purrr 1.0.0.
       ## ℹ Please use `map()` instead.
       ##   # Previously
       ##   rerun(1000000, mao())
       ## 
       ##   # Now
       ##   map(1:1000000, ~ mao())
       ## This warning is displayed once every 8 hours.
       ## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.

       mean(!map_lgl(maos, tem_as))

       ## [1] 0,488336

  2. Qual a probabilidade de obter $4$ ases?

     • A ordem das cartas não importa.

     • Existe uma mão com $4$ ases para cada uma das outras $28$ cartas. Ou seja, existem $28$ mãos com $4$ ases.

     • Logo, a resposta é

       $$\frac{28}{\binom{32}{5}} = \frac{28}{201.376} \approx 0{,}000139$$

     • Uma probabilidade de pouco mais de um décimo de milésimo.

     • Testar se a mão tem $4$ ases:

       tem_4_ases <- function(mao) {
       
         sum(str_starts(mao, 'A')) == 4
       
       }

     • Simular (usando as mesmas mãos geradas na resposta anterior):

       mean(map_lgl(maos, tem_4_ases))

       ## [1] 0,000145

  3. Qual a probabilidade de obter uma sequência (7 a J, 8 a Q, 9 a K, ou 10 a A) de naipes quaisquer?

     • São $4$ possibilidades para o primeiro número da sequência (7, 8, 9, 10).

     • Cada uma das $5$ cartas pode ter um de $4$ naipes, dando $4^5$ possibilidades.

     • Então, existem $4 \cdot 4^5 = 4^6 = 4.096$ sequências.

     • A resposta é

       $$\frac{4.096}{\binom{32}{5}} = \frac{4.096}{201.376} \approx 0{,}020340$$

     • Testar se a mão tem sequência:

       tem_seq <- function(mao) {
       
         all(c(7, 8, 9, 1, 'J') %in% str_sub(mao, 1, 1)) ||
         all(c(8, 9, 1, 'J', 'Q') %in% str_sub(mao, 1, 1)) ||
         all(c(9, 1, 'J', 'Q', 'K') %in% str_sub(mao, 1, 1)) ||
         all(c(1, 'J', 'Q', 'K', 'A') %in% str_sub(mao, 1, 1))
       
       }

     • Simular (usando as mesmas mãos geradas na primeira resposta):

       mean(map_lgl(maos, tem_seq))

       ## [1] 0,020388

  4. Qual a probabilidade de obter uma sequência (7 a J, 8 a Q, 9 a K, ou 10 a A) do mesmo naipe?

     • Cada naipe tem $4$ sequências possíveis.

     • O total de sequências do mesmo naipe, então, é $4 \cdot 4 = 16$.

     • A resposta é

       $$\frac{16}{\binom{32}{5}} = \frac{16}{201.376} \approx 0{,}000079$$

     • É mais improvável obter uma sequência do mesmo naipe do que obter $4$ ases.

     • Testar se a mão tem sequência do mesmo naipe:

       tem_seq_naipe <- function(mao) {
       
         tem_seq(mao) && (
           all(str_ends(mao, '♥')) ||
           all(str_ends(mao, '♦')) ||
           all(str_ends(mao, '♠')) ||
           all(str_ends(mao, '♣'))
         )
       
       }

     • Simular:

       mean(map_lgl(maos, tem_seq_naipe))

       ## [1] 0,000061

7.12.3 Dados

• Calcule as seguintes probabilidades teoricamente e através de simulações.

  1. Você lança um dado não-viciado $6$ vezes. Qual a probabilidade de que saiam os $6$ números?

  2. Idem, se você lançar o dado $10$ vezes.

7.13 Vídeo 2

7.14 Probabilidade condicional

• Em um mesmo experimento, saber que um evento $B$ aconteceu pode dar informação sobre um outro evento $A$.

• Por exemplo, ao lançar um dado, a probabilidade de $A$ — conseguir um $6$ — é de $1/6$.

• Se formos informados que o evento $B$ — o lançamento deu um número maior que $3$ — ocorreu, então a probabilidade de ter conseguido um $6$ passa para $1/3$.

• Escrevemos

  $$P(A) = 1/6$$

  e

  $$P(A \mid B) = 1/3$$

• $P(A \mid B)$ é a probabilidade de $A$ ocorrer, dado que $B$ ocorreu.

• É uma probabilidade condicional. Estamos condicionando sobre $B$.

7.14.1 Exemplo: Titanic

• A seguinte tabela mostra as quantidades de pessoas no Titanic, categorizadas como sobreviventes ou não, e divididas pela classe:

  ##           Classe
  ## Sobreviveu    1    2    3 Tripulação Total
  ##      Não    122  167  528        673  1490
  ##      Sim    203  118  178        212   711
  ##      Total  325  285  706        885  2201

Probabilidade de ser tripulante

• Escolha uma das $2.201$ pessoas ao acaso.

• Qual é a probabilidade de a pessoa escolhida ser um tripulante?

• Esta é uma probabilidade não-condicional: basta dividir o total de tripulantes pelo total de pessoas:

  $$P(\text{tripulante}) = \frac {885} {2.201}$$

• A tabela está na variável tit_tab. Em R, podemos indexar uma tabela pelos nomes. O primeiro índice corresponde à linha, o segundo à coluna:

  ptrip <- 
    tit_tab['Total', 'Tripulação'] / tit_tab['Total', 'Total']
  
  ptrip

  ## [1] 0,40209

Probabilidade de não ser tripulante

• Escolha uma das $2.201$ pessoas ao acaso.

• Qual é a probabilidade de a pessoa escolhida não ser um tripulante?

• Esta é uma probabilidade não-condicional: basta dividir o total de não-tripulantes pelo total de pessoas:

  $$P(\text{não-tripulante}) = \frac {325 + 285 + 706} {2.201}$$

• Em R, podemos selecionar várias células de uma tabela; basta usar um vetor como índice:

  ntrip <- sum(tit_tab['Total', c('1', '2', '3')])
  
  ntrip / tit_tab['Total', 'Total']

  ## [1] 0,59791

• Mas nem era preciso fazer este cálculo. Basta perceber que “ser tripulante” e “ser não-tripulante” são eventos complementares. Daí,

  $$P(\text{não-tripulante}) = 1 - P(\text{tripulante})$$

  1 - ptrip

  ## [1] 0,59791

Probabilidade de sobreviver

• Escolha uma das $2.201$ pessoas ao acaso.

• Qual é a probabilidade de a pessoa escolhida ter sobrevivido?

• Esta é uma probabilidade não-condicional: basta dividir o total de sobreviventes pelo total de pessoas:

  $$P(\text{sobrevivente}) = \frac {711} {2.201}$$

  tit_tab['Sim', 'Total'] / tit_tab['Total', 'Total']

  ## [1] 0,323035

Probabilidade de ser de primeira classe

• Escolha uma das $2.201$ pessoas ao acaso.

• Qual é a probabilidade de a pessoa escolhida ser da primeira classe?

• Esta é uma probabilidade não-condicional: basta dividir o total de passageiros da primeira classe pelo total de pessoas:

  $$P(\text{1ª classe}) = \frac {325} {2.201}$$

  tit_tab['Total', '1'] / tit_tab['Total', 'Total']

  ## [1] 0,1476602

Probabilidade de sobreviver E ser de primeira classe

• Escolha uma das $2.201$ pessoas ao acaso.

• Qual é a probabilidade de a pessoa escolhida ter sobrevivido e ser da primeira classe?

• Isto é uma probabilidade conjunta — a probabilidade de dois eventos terem ocorrido ao mesmo tempo. Ainda não é uma probabilidade condicional.

• Queremos saber a proporção de pessoas, do total de pessoas a bordo, que eram de primeira classe e sobreviveram.

  $$P(\text{sobrevivente da 1ª classe}) = \frac {203} {2.201}$$

  tit_tab['Sim', '1'] / tit_tab['Total', 'Total']

  ## [1] 0,0922308

Probabilidade de uma pessoa da primeira classe sobreviver

• Escolha uma das $2.201$ pessoas ao acaso.

• Qual é a probabilidade de a pessoa escolhida ter sobrevivido, dado que a pessoa estava na primeira classe?

• Isto é uma probabilidade condicional, escrita como

  $$P(\text{sobrevivente } \mid \text{ 1ª classe})$$

• Cuidado, agora.

• Já sabemos que a pessoa é da primeira classe. Logo, restringimos o universo a estas 325 pessoas. O denominador vai ser o total de passageiros da primeira classe:

  $$P(\text{sobrevivente } \mid \text{ 1ª classe}) = \frac {203} {325}$$

  tit_tab['Sim', '1'] / tit_tab['Total', '1'] 

  ## [1] 0,6246154

• Perceba que

  $$P(\text{sobreviveu} \mid \text{1ª classe} )$$

  é o mesmo que

  $$\frac{P(\text{sobreviveu } \cap \text{ 1ª classe})}{P(\text{1ª classe})}$$

Probabilidade de um sobrevivente ser da primeira classe

• Escolha uma das $2.201$ pessoas ao acaso.

• Qual é a probabilidade de a pessoa escolhida ser da primeira classe, dado que ela sobreviveu?

• Isto é outra probabilidade condicional, escrita como

  $$P(\text{1ª classe } \mid \text{ sobreviveu})$$

• Não é a mesma probabilidade que $P(\text{sobreviveu} \mid \text{1ª classe})$.

• Em português:

  • $P(\text{sobreviveu} \mid \text{1ª classe})$ é a probabilidade de

    • A pessoa sobreviver, dado que era da primeira classe;

    • Equivalentemente: alguém da primeira classe sobreviver.

  • $P(\text{1ª classe } \mid \text{ sobreviveu})$ é a probabilidade de

    • A pessoa ter sido da primeira classe, dado que sobreviveu;

    • Equivalentemente: alguém que sobreviveu ter sido da primeira classe.

  • Releia até entender.

• Agora, restringimos o universo às pessoas que sobreviveram. Dentre estas, quantas são da primeira classe?

  $$P(\text{1ª classe } \mid \text{ sobreviveu}) = \frac {203} {711}$$

  tit_tab['Sim', '1'] / tit_tab['Sim', 'Total']

  ## [1] 0,2855134

  Este é um exemplo de que $P(A \mid B)$ pode ser diferente de $P(B \mid A)$.

7.14.2 Definição de probabilidade condicional

• Como vimos nos exemplos, para calcular $P(A \mid B)$, restringimos o universo aos elementos onde $B$ acontece, e, deste universo, verificamos quantos elementos também correspondem a $A$ acontecer — isto é, elementos onde $A \cap B$ acontece.

• Em termos de frequência relativa:

  $$\frac{\text{ocorrências de } A \cap B}{\text{ocorrências de }B}$$

• Em termos de probabilidade, a definição é

  $$P(A \mid B) \quad=\quad \frac{P(A \cap B)}{P(B)}$$

7.14.3 Exercícios

No Titanic,

1. Qual a probabilidade de um tripulante sobreviver?

2. Qual a probabilidade de um sobrevivente ser tripulante?

3. Qual a probabilidade de um não-tripulante sobreviver?

4. Qual a probabilidade de um sobrevivente não ser tripulante?

5. Compare as probabilidades condicionais de uma pessoa sobreviver dado que

   1. Ela estava na 1ª classe. (Já calculada no exemplo acima: $0{,}62$.)

   2. Ela estava na 2ª classe.

   3. Ela estava na 3ª classe.

   4. Ela era da tripulação.

   Que conclusões você tira?

7.15 Probabilidade conjunta

• Imagine que queremos calcular a probabilidade de dois eventos $A$ e $B$ acontecerem ao mesmo tempo.

• Ou seja, queremos descobrir a probabilidade conjunta $P(A \cap B)$.

• Muitas vezes, é difícil calcular esta probabilidade diretamente.

• A fórmula para calcular $P(A \mid B)$ nos dá uma maneira de calcular $P(A \cap B)$:

  $$P(A \mid B) \;=\; \frac{P(A \cap B)}{P(B)} \quad\iff\quad P(A \cap B) \;=\; P(A \mid B) \cdot P(B)$$

• Ou, invertendo $A$ e $B$,

  $$P(B \mid A) \;=\; \frac{P(A \cap B)}{P(A)} \quad\iff\quad P(A \cap B) \;=\; P(B \mid A) \cdot P(A)$$

• Em palavras:

  • A probabilidade de $A$ e $B$ acontecerem juntos é a probabilidade de $A$ dado que $B$ aconteceu, multiplicada pela probabilidade de $B$.

  • Ou, invertendo $A$ e $B$, a probabilidade de $A$ e $B$ acontecerem juntos é a probabilidade de $B$ dado que $A$ aconteceu, multiplicada pela probabilidade de $A$.

7.16 Independência

• Mais acima, vimos que, para dois eventos independentes $A$ e $B$, a probabilidade conjunta $P(A \cap B)$ é igual a $P(A) \cdot P(B)$.

• Olhando para as fórmulas acima para a probabilidade conjunta, se $A$ e $B$ forem independentes, então

  $$\begin{aligned} P(A \cap B) &= P(A \mid B) \cdot P(B) \\ &= P(A) \cdot P(B) \end{aligned}$$

  o que nos diz que

  $$P(A \mid B) = P(A)$$

• Da mesma forma,

  $$P(B \mid A) = P(B)$$

• Em palavras: saber que um dos eventos ocorreu não altera a probabilidade do outro evento.

• Qualquer uma das $3$ igualdades pode ser tomada como a definição formal de eventos independentes.

7.16.1 Exemplos

Estar na primeira classe e sobreviver são independentes?

• A probabilidade de sobreviver, dado que a pessoa estava na 1ª classe, é

  $$P(\text{sobreviver} \mid \text{1ª classe}) = \frac{203}{325}$$

  tit_tab['Sim', '1'] / tit_tab['Total', '1']

  ## [1] 0,6246154

• Mas a probabilidade (incondicional) de sobreviver é

  $$P(\text{sobreviver}) = \frac{711}{2.201}$$

  tit_tab['Sim', 'Total'] / tit_tab['Total', 'Total']

  ## [1] 0,323035

• Como as probabilidades são diferentes, os eventos não são independentes.

• Verifique se $P(\text{sobreviver} \cap \text{1ª classe}) = P(\text{sobreviver}) \cdot P(\text{1ª classe})$.

Faltas e turno de trabalho

• Numa empresa:

  • $75$ funcionários trabalham no turno diurno, com um número de faltas de $3$ por semana.

  • $25$ funcionários trabalham no turno noturno, com um número de faltas de $1$ por semana.

  • Faltar é independente do turno de trabalho?

• Vamos construir uma tabela:

  faltas <- array(
    c(3, 1, 72, 24),
    dim = c(2, 2)
  ) %>% 
    addmargins()
  
  dimnames(faltas) = list(
      'Turno' = c('Diurno', 'Noturno', 'Total'),
      'Presença' = c('Faltou', 'Presente', 'Total')
    )
  
  faltas

  ##          Presença
  ## Turno     Faltou Presente Total
  ##   Diurno       3       72    75
  ##   Noturno      1       24    25
  ##   Total        4       96   100

• A probabilidade (incondicional) de faltar é

  $$P(\text{Faltou}) = \frac{4} {100}$$

  faltas['Total', 'Faltou'] / faltas['Total', 'Total']

  ## [1] 0,04

• A probabilidade de faltar no turno diurno é

  $$P(\text{Faltou} \mid \text{Diurno}) = \frac{3} {75}$$

  faltas['Diurno', 'Faltou'] / faltas['Diurno', 'Total']

  ## [1] 0,04

• Como as probabilidades são iguais, os eventos são independentes.

• Verifique que $P(\text{Faltou}) = P(\text{Faltou} \mid \text{Noturno})$.

7.17 Probabilidade total

7.17.1 Exemplo

• Dentre $80$ homens, $30$ têm olhos azuis.

• Dentre $50$ mulheres, $20$ têm olhos azuis.

• Neste grupo de pessoas, qual a probabilidade de ter olhos azuis?

• Homens e mulheres formam uma partição deste grupo — i.e., cada pessoa só pode ser homem ou mulher (não ambos) e cada pessoa precisa ser homem ou mulher.

• O evento “ter olhos azuis” se subdivide em dois casos mutuamente exclusivos:

  1. Ter olhos azuis e ser homem;

  2. Ter olhos azuis e ser mulher.

• Vamos chamar os eventos de

  • $A$ = ter olhos azuis

  • $H$ = ser homem

  • $M$ = ser mulher

• Calculamos a probabilidade $P(A)$ somando as probabilidades dos dois casos:

  $$\begin{aligned} P(A) &= P(A \cap H) + P(A \cap M) \end{aligned}$$

• Então,

  $$\begin{aligned} P(A) = \frac{30}{130} + \frac{20}{130} = \frac{50}{130} \approx 0{,}39 \end{aligned}$$

• Ou, antes de somar, podemos transformar as probabilidades conjuntas em produtos de uma probabilidade condicional por uma probabilidade não-condicional:

  $$\begin{aligned} P(A) &= P(A \cap H) + P(A \cap M) \\ &= P(A \mid H) P(H) + P(A \mid M) P(M) \end{aligned}$$

• O que nos dá o mesmo resultado:

  $$\begin{aligned} P(A) &= \frac{30}{80} \cdot \frac{80}{130} + \frac{20}{50} \cdot \frac{50}{130} \\ &= \frac{50}{130} \\ &\approx 0{,}39 \end{aligned}$$

7.18 Teorema de Bayes

7.18.1 Exemplo

• De todos os emails, $60\%$ são spam:

  $$P(\text{spam}) = 0{,}6$$

• De todos os emails que são spam, $90\%$ contêm a palavra “compre”:

  $$P(\text{compre} \mid \text{spam}) = 0{,}9$$

• De todos os emails (spam ou não), $70\%$ contêm a palavra “compre”:

  $$P(\text{compre}) = 0{,}7$$

• Você acaba de receber um email. Antes de você abri-lo, qual a probabilidade de o email ser spam?

• Bem, na ausência de informação adicional, $P(\text{spam}) = 0{,}6$.

• Você abre o email. Ele contém a palavra “compre”.

• Agora, qual a probabilidade de ser spam?

  $$P(\text{spam} \mid \text{compre}) = {}?$$

• Lembre-se de que

  $$P(\text{compre} \cap \text{spam}) = P(\text{spam} \mid \text{compre}) \cdot P(\text{compre})$$

• Mas também

  $$P(\text{compre} \cap \text{spam}) = P(\text{compre} \mid \text{spam}) \cdot P(\text{spam})$$

• As duas expressões são iguais:

  $$P(\text{spam} \mid \text{compre}) \cdot P(\text{compre}) = P(\text{compre} \mid \text{spam}) \cdot P(\text{spam})$$

• Isolando o termo que queremos descobrir:

  $$P(\text{spam} \mid \text{compre}) = \frac{P(\text{compre} \mid \text{spam}) \cdot P(\text{spam})}{P(\text{compre})}$$

• Substituindo os valores:

  $$P(\text{spam} \mid \text{compre}) = \frac{0{,}9 \cdot 0{,}6}{0{,}7} \approx 0{,}77$$

• Isto é inferência bayesiana:

  1. Começamos com uma probabilidade não-condicional: a priori, $P(\text{spam}) = 0{,}6$;

  2. Obtivemos nova informação: o email contém “compre”;

  3. Usamos esta informação para calcular uma probabilidade condicional, a posteriori:

  $$P(\text{spam} \mid \text{compre}) = \frac{P(\text{compre} \mid \text{spam}) \cdot P(\text{spam})}{P(\text{compre})}$$

• Perceba que, para isso, precisamos da probabilidade não-condicional $P(\text{compre})$ (no denominador).

7.18.2 No geral

$$P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)}$$

• E se você não souber $P(B)$?

• Use o teorema da probabilidade total:

  $$P(B) = P(B \cap A_1) + P(B \cap A_2) + \cdots + P(B \cap A_n)$$ onde os $A_i$ formam uma partição da população.

• Isto equivale a

  $$P(B) = P(B \mid A_1)P(A_1) + P(B \mid A_2)P(A_2) + \cdots + P(B \mid A_n)P(A_n)$$

7.18.3 Outro exemplo

• Uma doença rara afeta $5$ pessoas em $100.000$.

• O exame que detecta a doença tem precisão de $99{,}9\%$; i.e., quando uma pessoa está doente, o exame dá positivo $99{,}9\%$ das vezes.

• Quando uma pessoa não está doente, o exame dá positivo $1\%$ das vezes. Este caso é um falso positivo.

• Você faz o exame, e o resultado é positivo.

• Dado este resultado, qual a probabilidade de você ter a doença?

• Vamos nomear os eventos:

  • $D = {}$ você está doente;

  • $ND = {}$ você não está doente;

  • $+ = {}$ o exame deu positivo;

  • $- = {}$ o exame deu negativo.

• Vamos usar Bayes:

  $$P(D \mid +) = \frac{P(+ \mid D)P(D)}{P(+)}$$

• $P(+ \mid D) = 0{,}999$, pelo enunciado.

• $P(D) = 0{,}00005$, pelo enunciado.

• Daí, $P(ND) = 1 - P(D) = 0{,}99995$.

• Não temos $P(+)$, mas podemos achar usando o teorema da probabilidade total, lembrando que o enunciado diz que $P(+ \mid ND) = 0{,}01$:

  $$\begin{aligned} P(+) &= P(+ \cap D) \;+\; P(+ \cap ND) \\ &= P(+ \mid D)P(D) \;+\; P(+ \mid ND)P(ND) \\ &= 0{,}999 \cdot 0{,}00005 \;+\; 0{,}01 \cdot 0{,}99995 \\ &= 0{,}01004945 \end{aligned}$$

• Inserindo os valores no teorema de Bayes:

  $$\begin{aligned} P(D \mid +) &= \frac{P(+ \mid D)P(D)}{P(+)} \\ &= \frac{0{,}999 \cdot 0{,}00005}{0{,}01004945} \\ &= 0{,}00497 \end{aligned}$$

• A probabilidade de estar doente é menos do que $0{,}5\%$!

• Você provavelmente esperava uma probabilidade maior.

• Qual das $3$ probabilidades usadas no cálculo fez o resultado ser tão pequeno?

  • $P(+ \mid D)$?

  • $P(D)$?

  • $P(+)$?