Capítulo 5 Visualização com ggplot2 (continuação)

Busque mais informações sobre os pacotes tidyverse e ggplot2 nas referências recomendadas.

5.1 Vídeo 1

5.2 Boxplots

5.2.1 Conjunto de dados

Vamos continuar a trabalhar com os dados sobre as horas de sono de alguns mamíferos:
```
sono <- msleep %>% 
  select(name, vore, order, sleep_total)

sono
```

5.2.2 Mediana e quartis

Para entender boxplots, precisamos, antes, entender algumas medidas.

Se tomarmos as quantidades de horas de sono de todos os animais do conjunto de dados e classificarmos estas quantidades em ordem crescente, vamos ter:

horas <- sono %>% 
  pull(sleep_total) %>% 
  sort()

horas

##  [1]  1,9  2,7  2,9  3,0  3,1  3,3  3,5  3,8  3,9  4,0  4,4  5,2  5,3  5,3  5,4  5,6
## [17]  6,2  6,3  6,3  7,0  7,7  8,0  8,3  8,4  8,4  8,6  8,7  8,7  8,9  9,1  9,1  9,4
## [33]  9,4  9,5  9,6  9,7  9,8  9,8 10,0 10,1 10,1 10,1 10,3 10,3 10,4 10,6 10,9 11,0
## [49] 11,0 11,1 11,3 11,5 12,1 12,5 12,5 12,5 12,5 12,8 12,8 13,0 13,5 13,7 13,8 14,2
## [65] 14,3 14,4 14,4 14,5 14,6 14,9 14,9 15,6 15,8 15,8 15,9 16,6 17,0 17,4 18,0 18,1
## [81] 19,4 19,7 19,9

Quantos valores são?
```
length(horas)
```
```
## [1] 83
```
O valor que está bem no meio desta fila — i.e., na posição \(42\) — é a mediana:
```
horas[ceiling(length(horas) / 2)]
```
```
## [1] 10,1
```
Em R:
```
median(horas)
```
```
## [1] 10,1
```
Mediana e média são coisas muito diferentes.

Por acaso, neste exemplo, a média das horas é próxima da mediana:
```
mean(horas)
```
```
## [1] 10,43373
```
Isto costuma acontecer quando a distribuição dos dados é aproximadamente simétrica.

Os quartis são os valores que estão nas posições \(\frac14\), \(\frac12\) e \(\frac34\) da fila. São o primeiro, segundo e terceiro quartis, respectivamente.

horas[
  c(
    ceiling(length(horas) / 4),
    ceiling(length(horas) / 2),
    ceiling(3 * length(horas) / 4)
  )
]

## [1]  7,7 10,1 13,8

Sim, a mediana é o segundo quartil.
Em R, a função quantile generaliza esta idéia: dado um número \(q\) entre \(0\) e \(1\), o quantil (com “N”) \(q\) é o elemento que está na posição que corresponde à fração \(q\) da fila ordenada.
```
horas %>% quantile(c(.25, .5, .75))
```
```
##   25%   50%   75% 
##  7,85 10,10 13,75
```
Na verdade, R tem \(9\) algoritmos diferentes para calcular os quantis de uma amostra! Leia a ajuda da função quantile para conhecê-los.
As diferenças entre nossos cálculos “à mão” e os resultados retornados por quantile são porque, em algumas situações, quantile calcula uma média ponderada entre elementos vizinhos. Por isso, quantile pode retornar valores que nem estão no vetor.

Em R, a função summary mostra o mínimo, os quartis (com “R”), a média, e o máximo de um vetor:

summary(horas)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1,90    7,85   10,10   10,43   13,75   19,90

5.2.3 Média \(\times\) mediana

Vamos ver um exemplo simples para entender a diferença entre a média e a mediana.
Imagine o seguinte vetor com as receitas mensais de algumas pessoas (em milhares de reais:)
```
receitas <- c(1, 2, 2, 3.5, 1, 4, 1)
```

Eis a mediana e a média deste vetor:

summary(receitas)[c('Median', 'Mean')]

##   Median     Mean 
## 2,000000 2,071429

A mediana e a média são bem próximas.
Imagine, agora, que adicionamos ao vetor um sujeito com receita mensal de \(100\) mil reais:
```
receitas <- c(1, 2, 2, 3.5, 1, 4, 1, 100)
```

Eis a nova mediana e a nova média:

summary(receitas)[c('Median', 'Mean')]

##  Median    Mean 
##  2,0000 14,3125

O sujeito com a receita de \(2\) mil reais continua no meio da fila, mas a média (que é a soma de todas as receitas, dividida pelo número de indivíduos) ficou muito diferente.
A receita do novo sujeito é um valor discrepante, ou, em inglês, um outlier.

Conclusão:

A mediana é robusta, pouco afetada por outliers.

A média é pouco robusta, muito sensível a outliers.

5.2.4 Intervalo interquartil (IQR) e outliers

Qual fração dos elementos está entre o primeiro e o terceiro quartis?

length(
  horas[between(horas, quantile(horas, .25), quantile(horas, .75))]
) /
length(
  horas
)

## [1] 0,4939759

Metade do total de elementos está entre o primeiro e o terceiro quartis.
Este é o chamado intervalo interquartil (interquartile range, em inglês).

No nosso vetor horas, os limites do IQR são

quantile(horas, c(.25, .75))

##   25%   75% 
##  7,85 13,75

O comprimento deste intervalo é calculado pela função IQR:
```
IQR(horas)
```
```
## [1] 5,9
```
Valores muito abaixo do primeiro quartil podem ser considerados discrepantes (outliers), mas quão abaixo?
A resposta (puramente convencional) é \(1{,}5 \times \text{IQR}\) abaixo do primeiro quartil.

No nosso vetor horas, isto significa valores abaixo de

limite_inferior <- quantile(horas, .25) - 1.5 * IQR(horas)

unname(limite_inferior)

## [1] -1

Neste caso, não há outliers:

horas[horas < limite_inferior]

## numeric(0)

Da mesma forma, valores muito acima do terceiro quartil podem ser considerados discrepantes (outliers), mas quão acima?
De novo, a resposta (puramente convencional) é \(1{,}5 \times \text{IQR}\) acima do terceiro quartil.

No nosso vetor horas, isto significa valores acima de

limite_superior <- quantile(horas, .75) + 1.5 * IQR(horas)

unname(limite_superior)

## [1] 22,6

Neste caso, também não há outliers:

horas[horas > limite_superior]

## numeric(0)

Outro exemplo: vamos tomar apenas os mamíferos onívoros:
```
onivoros <- sono %>% 
  filter(vore == 'omni')

onivoros
```

Vamos extrair o vetor de horas de sono:

horas <- onivoros %>% 
  pull(sleep_total)

horas

##  [1] 17,0 14,9 10,0 10,3  8,3  9,1 18,0 10,1 10,9  9,8  8,0 10,1  9,7  9,4 11,0  8,7
## [17]  9,6  9,1 15,6  8,9

Vamos calcular o primeiro e terceiro quartis:

quartis <- horas %>% 
  quantile(c(.25, .75))

quartis

##    25%    75% 
##  9,100 10,925

Vamos achar o IQR:
```
IQR(horas)
```
```
## [1] 1,825
```

E os limites a partir dos quais os valores são outliers:

limites <- quartis + c(-1, 1) * 1.5 * IQR(horas)

unname(limites)

## [1]  6,3625 13,6625

Existem outliers inferiores?
```
onivoros %>% 
  filter(sleep_total < limites[1])
```
Não.
Existem outliers superiores?
```
onivoros %>% 
  filter(sleep_total > limites[2])
```
Sim! Estes animais dormem demais em comparação com os outros onívoros.

5.2.5 Gerando boxplots

Um boxplot é uma representação visual dos valores que calculamos acima.

No ggplot2, a geometria geom_boxplot constrói boxplots:

sono %>% 
  ggplot(aes(y = sleep_total)) +
    geom_boxplot(fill = 'gray') +
    scale_x_continuous(breaks = NULL) +
    scale_y_continuous(breaks = seq(0, 20, 2))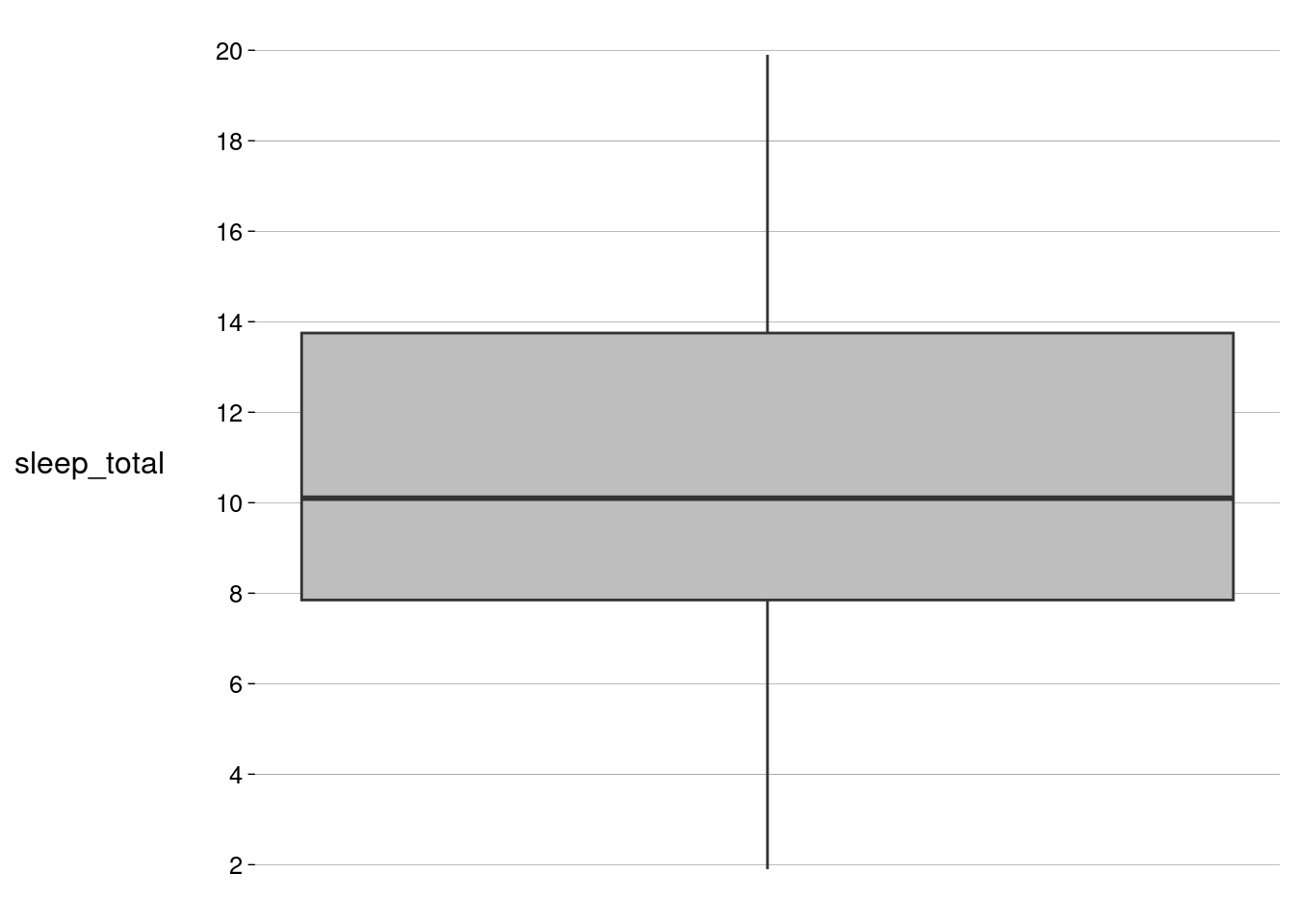

A caixa vai do valor do primeiro quartil (embaixo) até o terceiro quartil (em cima).
A linha horizontal dentro da caixa representa o valor da mediana.
As linhas verticais acima e abaixo da caixa (pitorescamente chamadas de “bigodes”) vão até o limite inferior (primeiro quartil \({}- 1{,}5 \times \text{IQR}\)) e até o limite superior (terceiro quartil \({}+ 1{,}5 \times \text{IQR}\)).
Neste boxplot, não há outliers.

Podemos usar a posição \(x\) para desenhar vários boxplots, um para cada dieta:

sono %>% 
  ggplot(aes(x = vore, y = sleep_total)) +
    geom_boxplot(fill = 'gray') +
    scale_y_continuous(breaks = seq(0, 20, 2))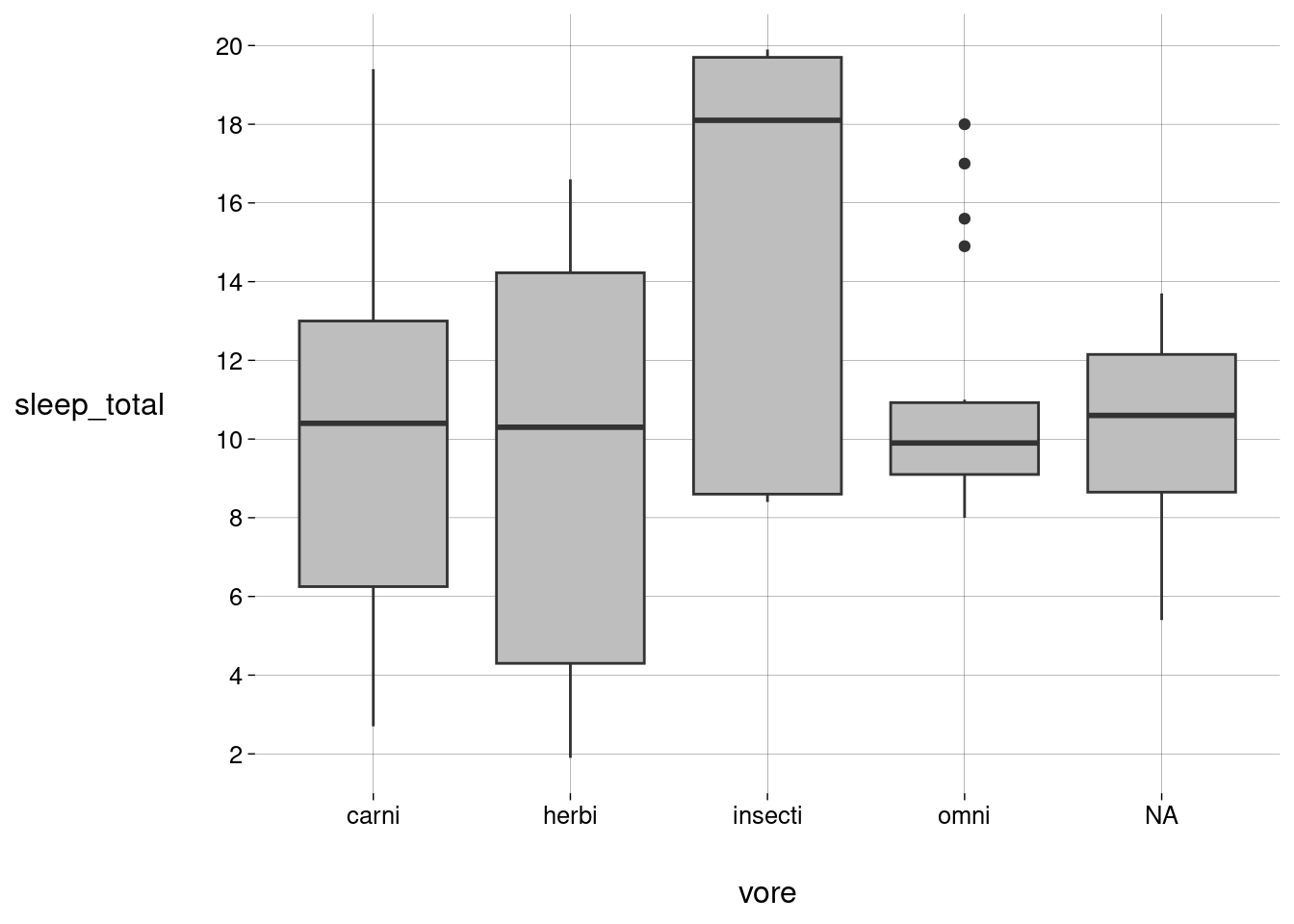

No boxplot de onívoros, os outliers aparecem como pontos isolados, acima da caixa, além dos alcances do bigode superior (aliás, onde está bigode superior?).
Boxplots lado a lado são úteis para compararmos grupos diferentes de dados.
Veja como, com exceção dos insetívoros, as medianas dos grupos são parecidas.
Veja como carnívoros, insetívoros e herbívoros apresentam maior variação, enquanto onívoros e animais sem dieta registrada apresentam menor variação.

Vamos combinar, em um só gráfico

Os pontos representando os animais,
Os boxplots,
As médias (que podem estar próximas ou distantes das medianas).

sono %>% 
  ggplot(aes(x = vore, y = sleep_total)) +
    geom_boxplot(fill = 'gray') +
    scale_y_continuous(breaks = seq(0, 20, 2)) +
    geom_point(
      color = 'blue', 
      alpha = .3
    ) +
    stat_summary(
      fun = mean, 
      geom = 'point', 
      color = 'red', 
      shape = 'cross', 
      size = 5,
      stroke = 1
    ) +
    labs(
      title = 'Sono total de diversos mamíferos, por dieta',
      subtitle = '(o X vermelho representa a média)',
      x = 'dieta',
      y = 'sono total\n(em horas)'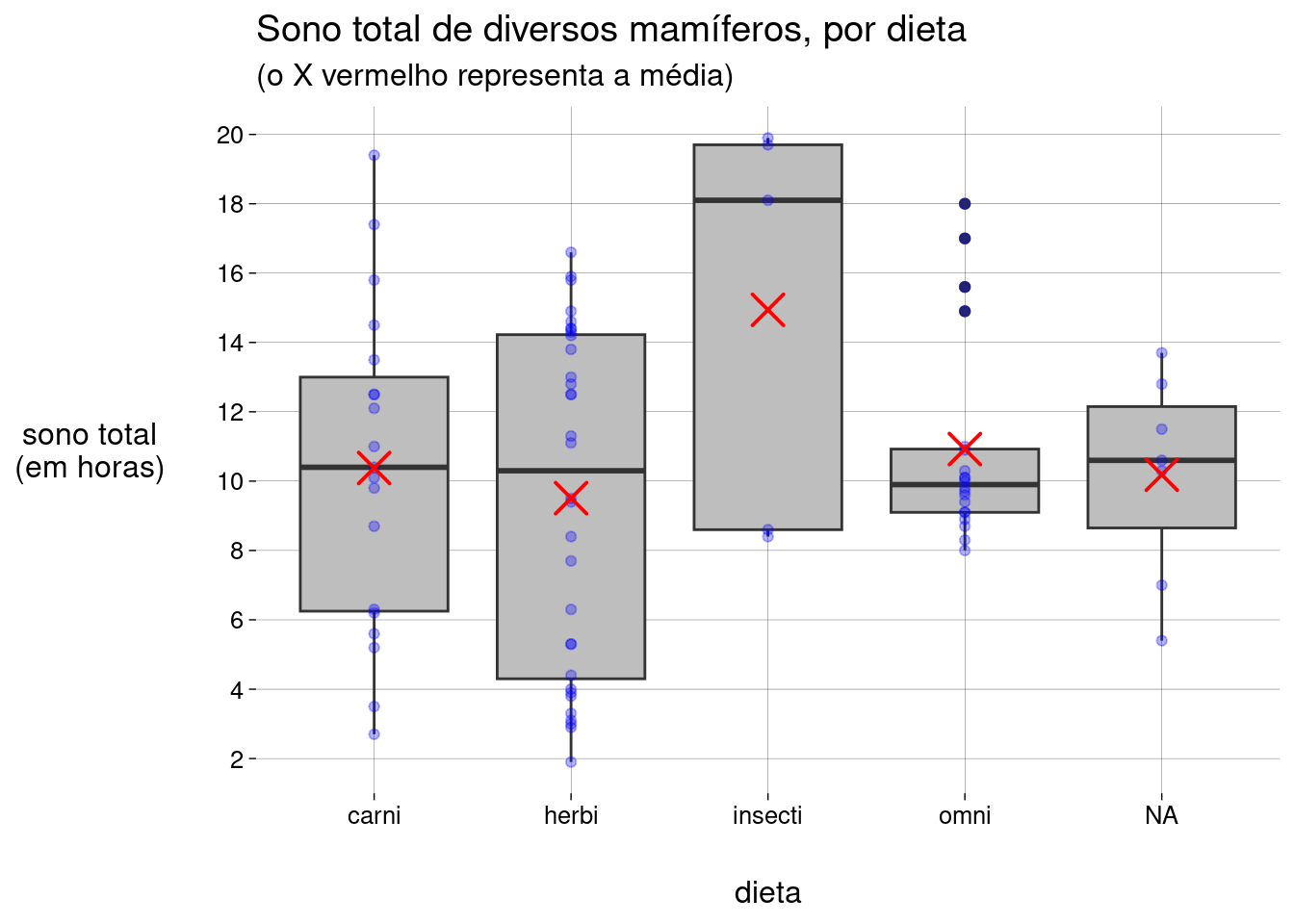
    )

Quando a caixa é longa, o IQR é grande, e os valores estão muito espalhados; é o caso dos herbívoros e insetívoros.
Quando a caixa é curta, o IQR é pequeno, e os valores estão pouco espalhados; é o caso dos onívoros. Como o IQR é pequeno, os \(4\) mamíferos com mais de \(14\) horas de sono são outliers.
Observe, ainda, como os outliers “puxam” a média dos onívoros para cima.

5.3 Vídeo 2

5.4 Gráficos de barras e de colunas

5.4.1 Conjunto de dados

O R tem um array de \(3\) dimensões com dados sobre as cores dos cabelos e dos olhos de \(592\) alunos e alunas de uma universidade americana em \(1974\).

Se pedirmos para o R exibir os dados, veremos duas matrizes, uma para cada sexo:

HairEyeColor

## , , Sex = Male
## 
##        Eye
## Hair    Brown Blue Hazel Green
##   Black    32   11    10     3
##   Brown    53   50    25    15
##   Red      10   10     7     7
##   Blond     3   30     5     8
## 
## , , Sex = Female
## 
##        Eye
## Hair    Brown Blue Hazel Green
##   Black    36    9     5     2
##   Brown    66   34    29    14
##   Red      16    7     7     7
##   Blond     4   64     5     8

Vamos transformar este array em um data frame.
O array contém apenas os totais de cada classe. Vamos usar a função uncount para gerar uma linha para cada aluno:
```
df_orig <- as.data.frame(HairEyeColor) %>% 
  uncount(Freq) %>% 
  as_tibble()

df_orig
```
O ggplot2 e os outros pacotes do tidyverse foram projetados para trabalhar com data frames neste formato, com uma observação (um indivíduo, um elemento) por linha. É o chamado formato tidy.

Usando vetores com elementos nomeados, podemos traduzir o conteúdo do data frame para português:

cabelo <- c(
  'Brown' = 'castanhos',
  'Blond' = 'louros',
  'Black' = 'pretos',
  'Red' = 'ruivos'
)

olhos <- c(
  'Brown' = 'castanhos',
  'Blue' = 'azuis',
  'Hazel' = 'avelã',
  'Green' = 'verdes'
)

sexo <- c(
  'Male' = 'homem',
  'Female' = 'mulher'
)

df <- df_orig %>% 
  transmute(
    cabelos = cabelo[Hair],
    olhos = olhos[Eye],
    sexo = sexo[Sex]
  )

Um sumário:

df %>% dfSummary() %>% print()

Variável	Estatísticas / Valores	Freqs (% de Válidos)
cabelos [character]	1. castanhos 2. louros 3. pretos 4. ruivos	108 (18,2%) 286 (48,3%) 71 (12,0%) 127 (21,5%)
olhos [character]	1. avelã 2. azuis 3. castanhos 4. verdes	93 (15,7%) 215 (36,3%) 220 (37,2%) 64 (10,8%)
sexo [character]	1. homem 2. mulher	279 (47,1%) 313 (52,9%)

5.4.2 Gerando gráficos de barras

Um gráfico de barras contém uma barra para cada valor de uma variável categórica.
Usamos geom_bar para gerar um gráfico de barras de cores de cabelo: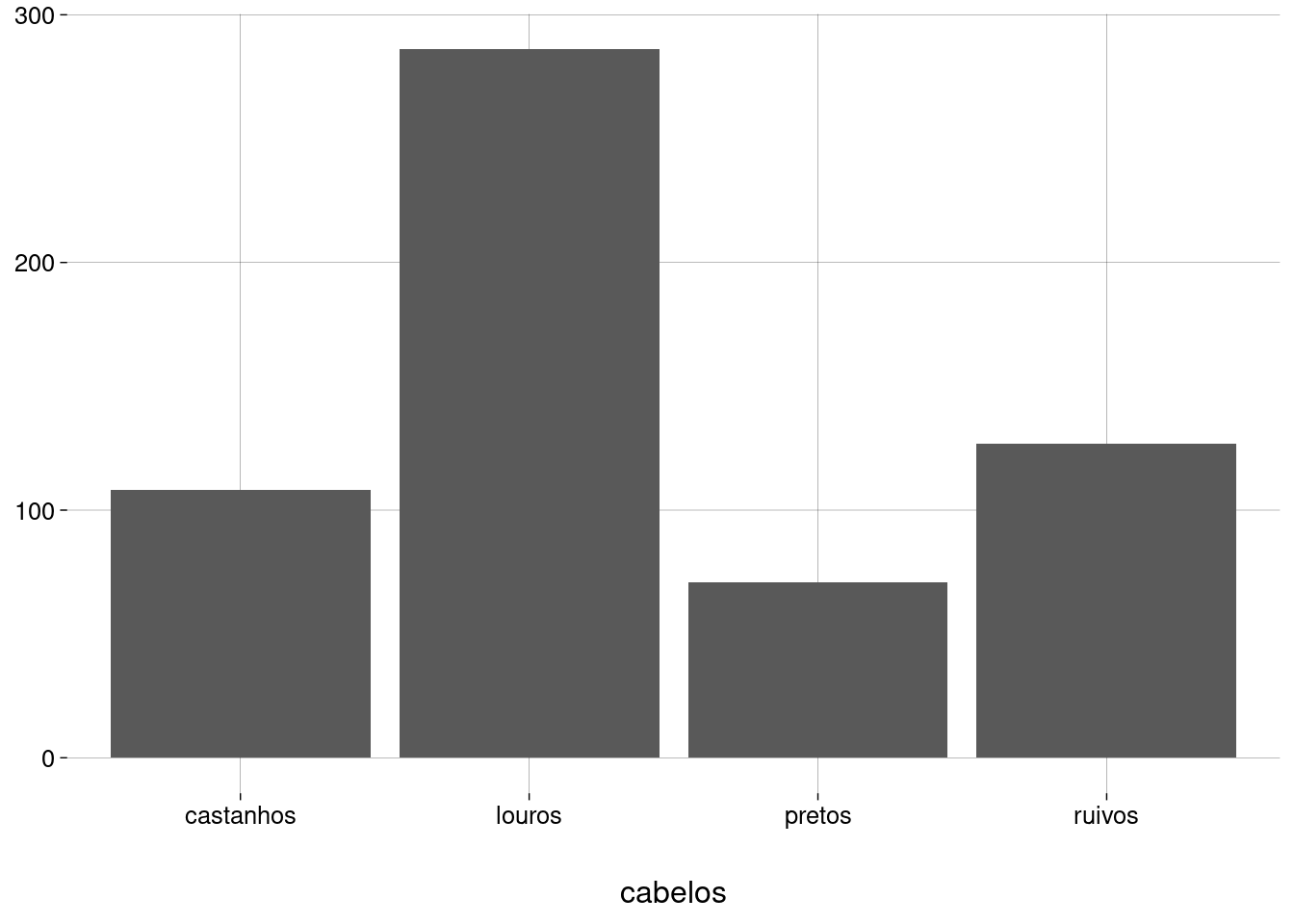
```
df %>% 
  ggplot(aes(x = cabelos)) +
    geom_bar() +
    labs(y = NULL)
```
Gráfico de barras \(\times\) histograma:
- Os dois tipos de gráficos mostram a frequência (quantidade de elementos) no eixo vertical.
- No gráfico de barras:
  - A variável é categórica (nominal).
  - Cada barra corresponde a um valor da variável.
  - As barras não se tocam, enfatizando o fato de que a variável é categórica.
- No histograma (veja o exemplo):
  - A variável é quantitativa (intervalar ou racional).
  - Cada barra corresponde a uma classe de valores da variável.
  - As barras se tocam, para enfatizar que as classes são contíguas.
Um gráfico de barras é mais legível quando as barras são mostradas em ordem crescente ou decrescente.
Embora os valores da variável cabelos sejam strings, podemos aplicar a eles funções que manipulam fatores.
A função fct_infreq, do pacote forcats, ordena os valores em ordem decrescente de frequência.

A função fct_rev, também do pacote forcats, inverte a ordenação.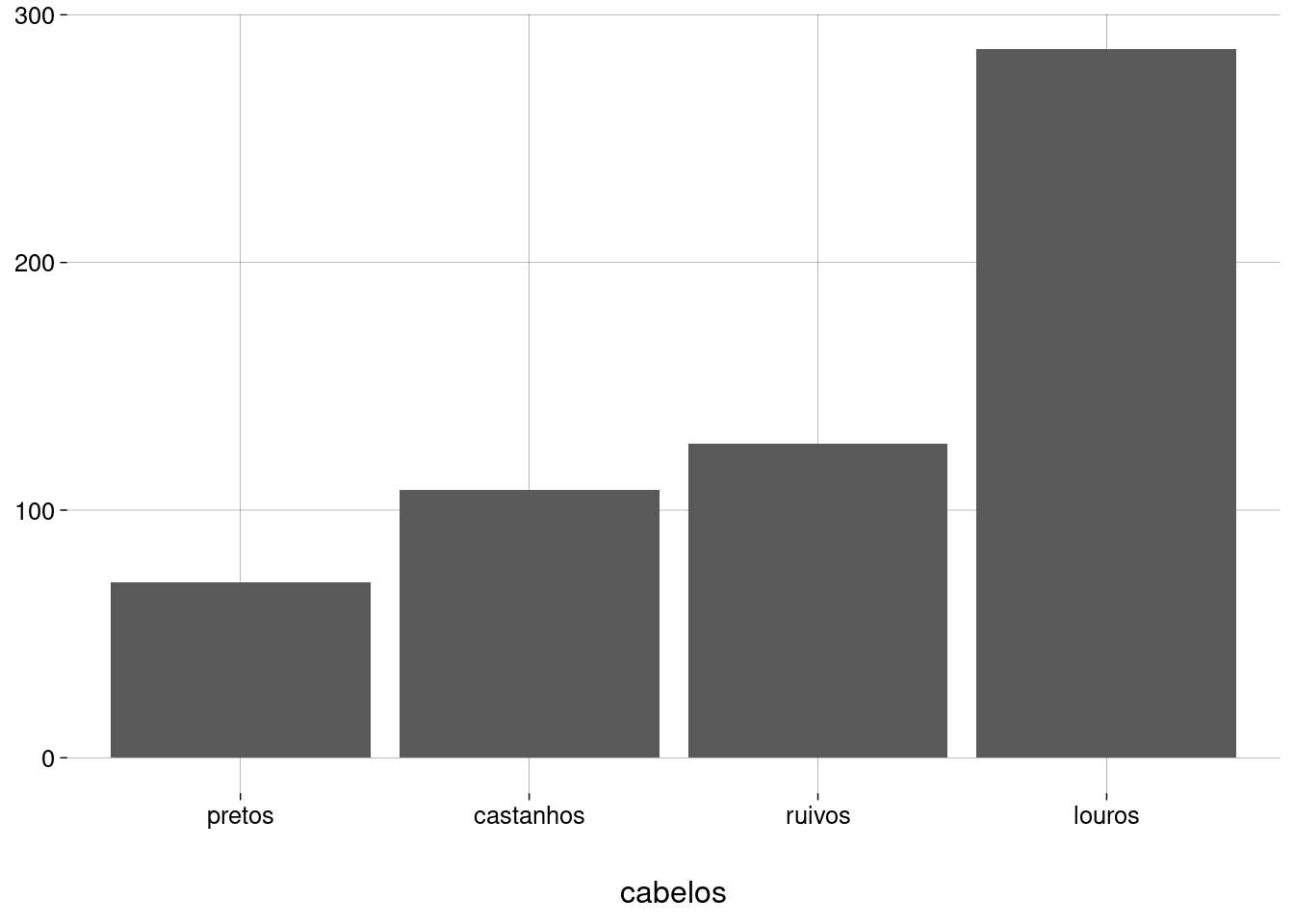

df %>% 
  ggplot(aes(x = fct_rev(fct_infreq(cabelos)))) +
    geom_bar() +
    labs(
      x = 'cabelos',
      y = NULL
    )

A posição \(x\) e a altura de cada barra são estéticas: a posição \(x\) representa a cor dos cabelos, e a altura representa a frequência daquela cor.

Vamos acrescentar mais uma estética: a cor de preenchimento vai representar o sexo.

df %>% 
  ggplot(aes(x = fct_rev(fct_infreq(cabelos)), fill = sexo)) +
    geom_bar() +
    labs(
      x = 'cabelos',
      y = NULL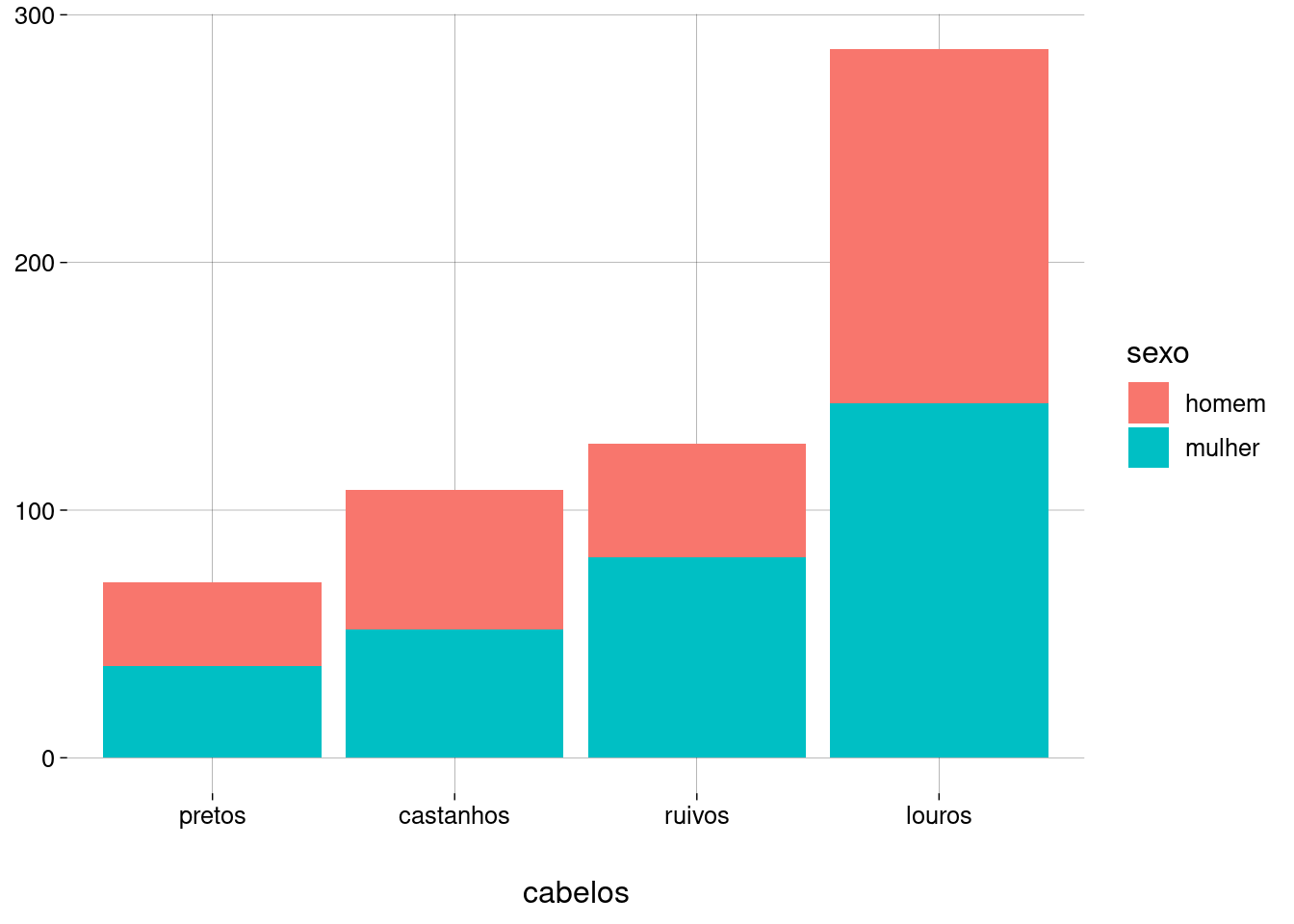
    )

Se a cor dos homens incomoda você, altere a escala que especifica o preenchimento (scale_fill_discrete):

df %>% 
  ggplot(aes(x = fct_rev(fct_infreq(cabelos)), fill = sexo)) +
    geom_bar() +
    scale_fill_discrete(type = c('blue', 'red')) +
    labs(
      x = 'cabelos',
      y = NULL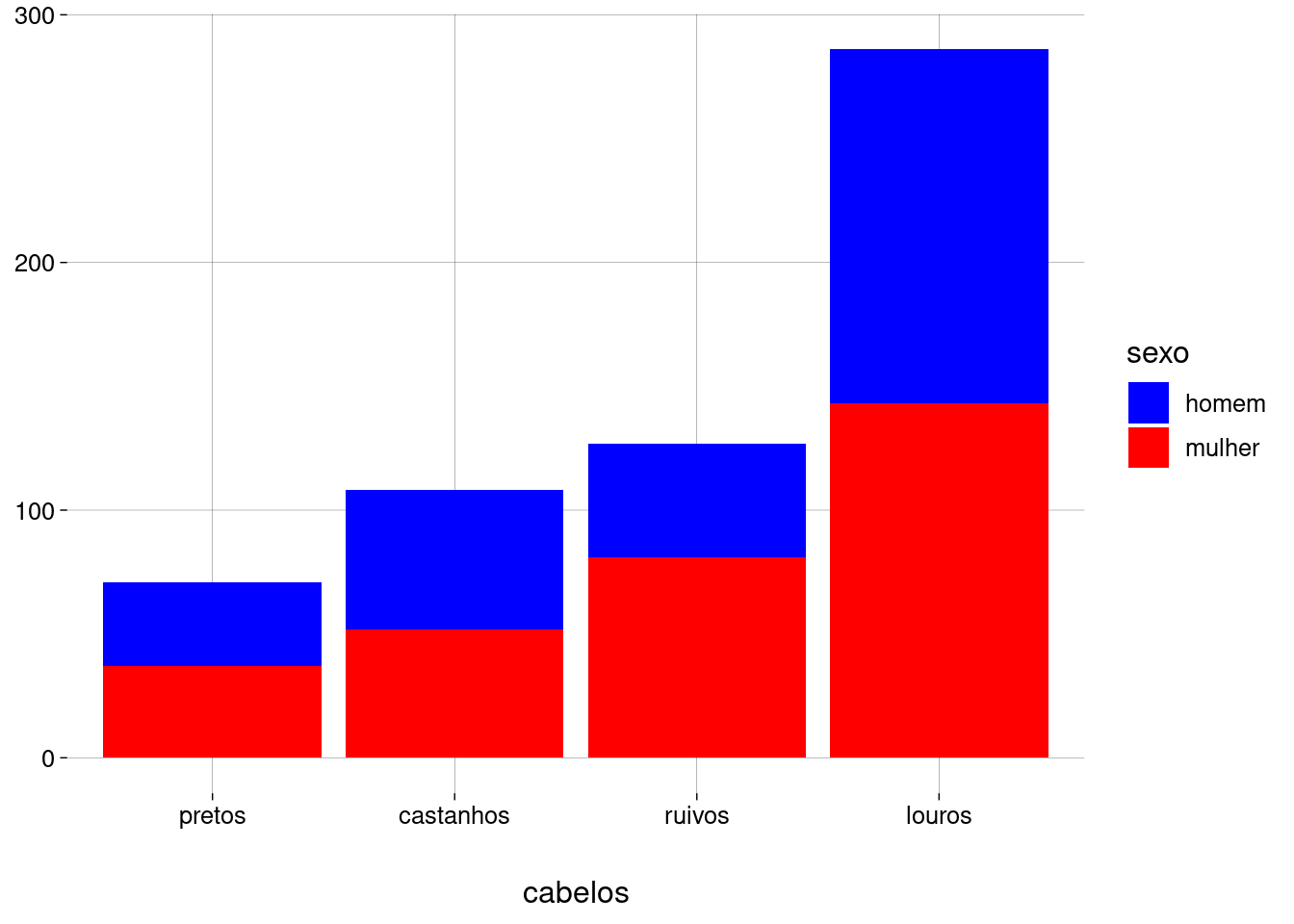
    )

Podemos fazer um gráfico de barras horizontais com coord_flip. Isto geralmente é útil quando os rótulos das barras são longos:

df %>% 
  ggplot(aes(x = fct_rev(fct_infreq(cabelos)), fill = sexo)) +
    geom_bar() +
    scale_fill_discrete(type = c('blue', 'red')) +
    labs(
      x = 'cabelos',
      y = NULL
    ) +
    coord_flip()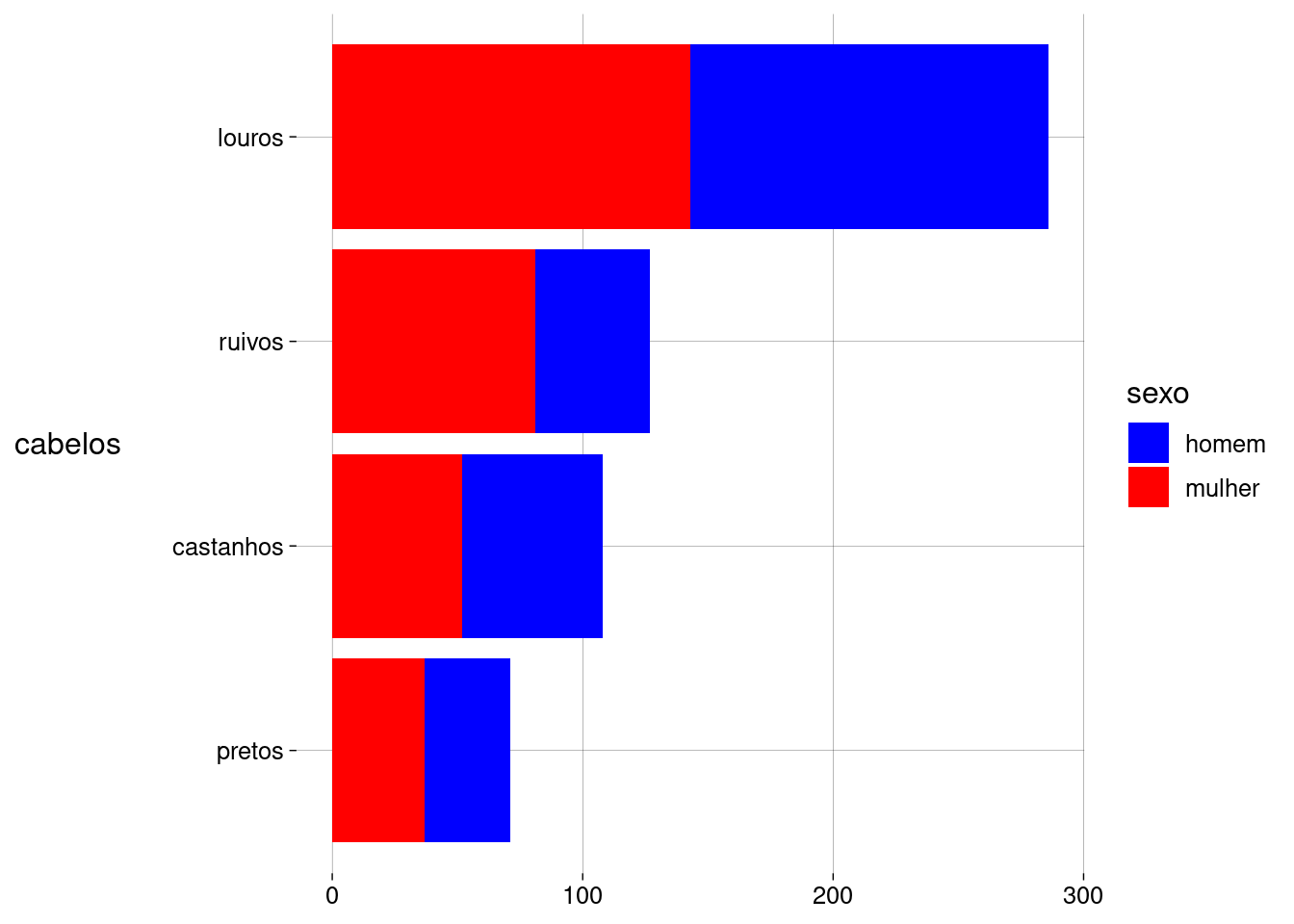

Você consegue dizer se há mais homens ou mulheres com cabelos pretos? E castanhos? E ruivos?
Se posicionarmos as barras lado a lado, fica mais fácil responder.

Usamos o argumento position = 'dodge' de geom_bar. “Dodge” significa “esquivar-se”, em inglês.

df %>% 
  ggplot(aes(x = fct_rev(fct_infreq(cabelos)), fill = sexo)) +
    geom_bar(position = 'dodge') +
    labs(
      x = 'cabelos',
      y = NULL
    ) +
    scale_fill_discrete(type = c('blue', 'red'))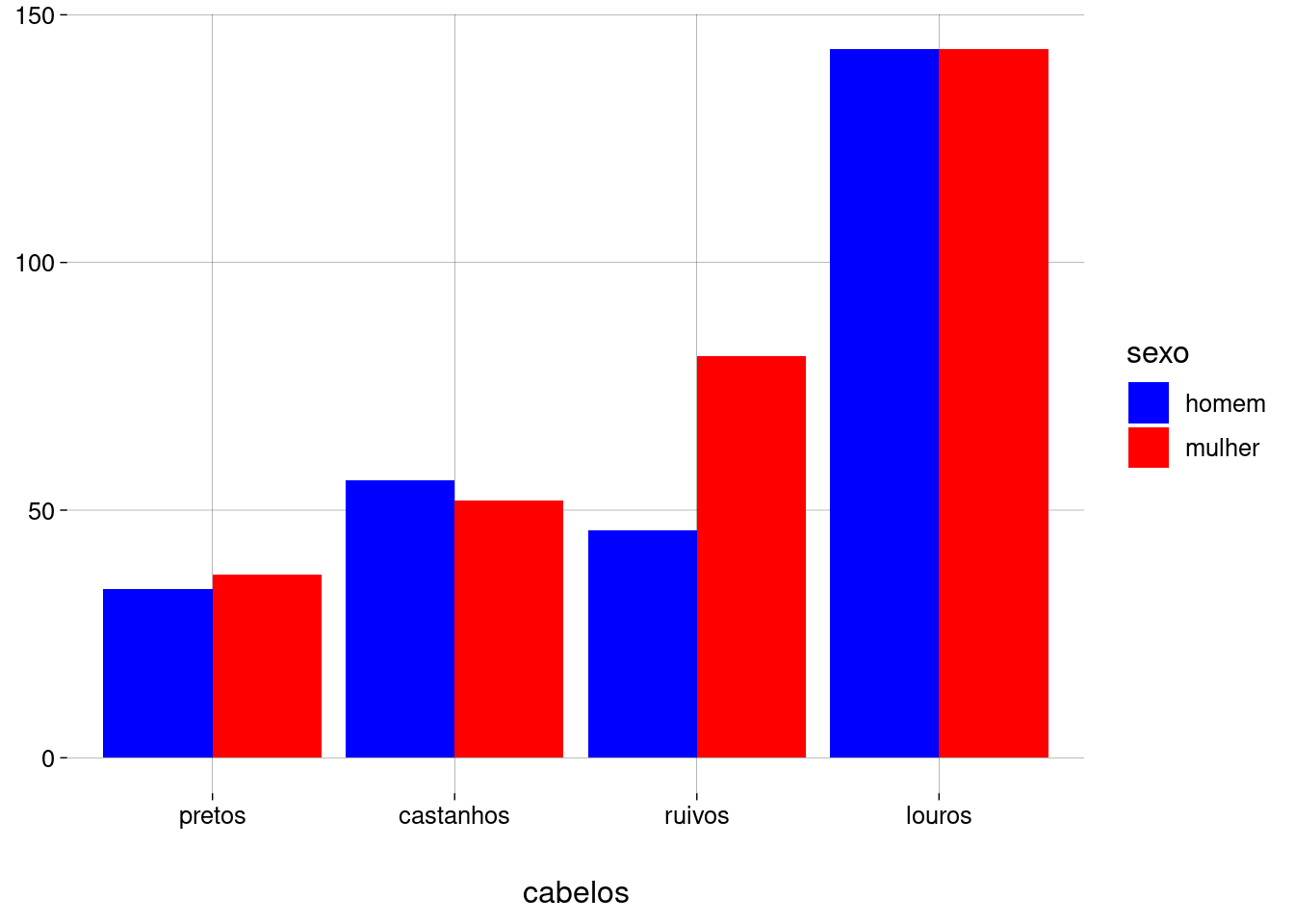

Agora vamos examinar a relação entre as cores dos olhos e as cores dos cabelos:

df %>% 
  ggplot(aes(x = fct_rev(fct_infreq(cabelos)), fill = olhos)) +
    geom_bar() +
    scale_fill_discrete(
      type = c('#908050', 'blue', 'brown', 'green')
    ) +
    labs(
      x = 'cabelos',
      y = NULL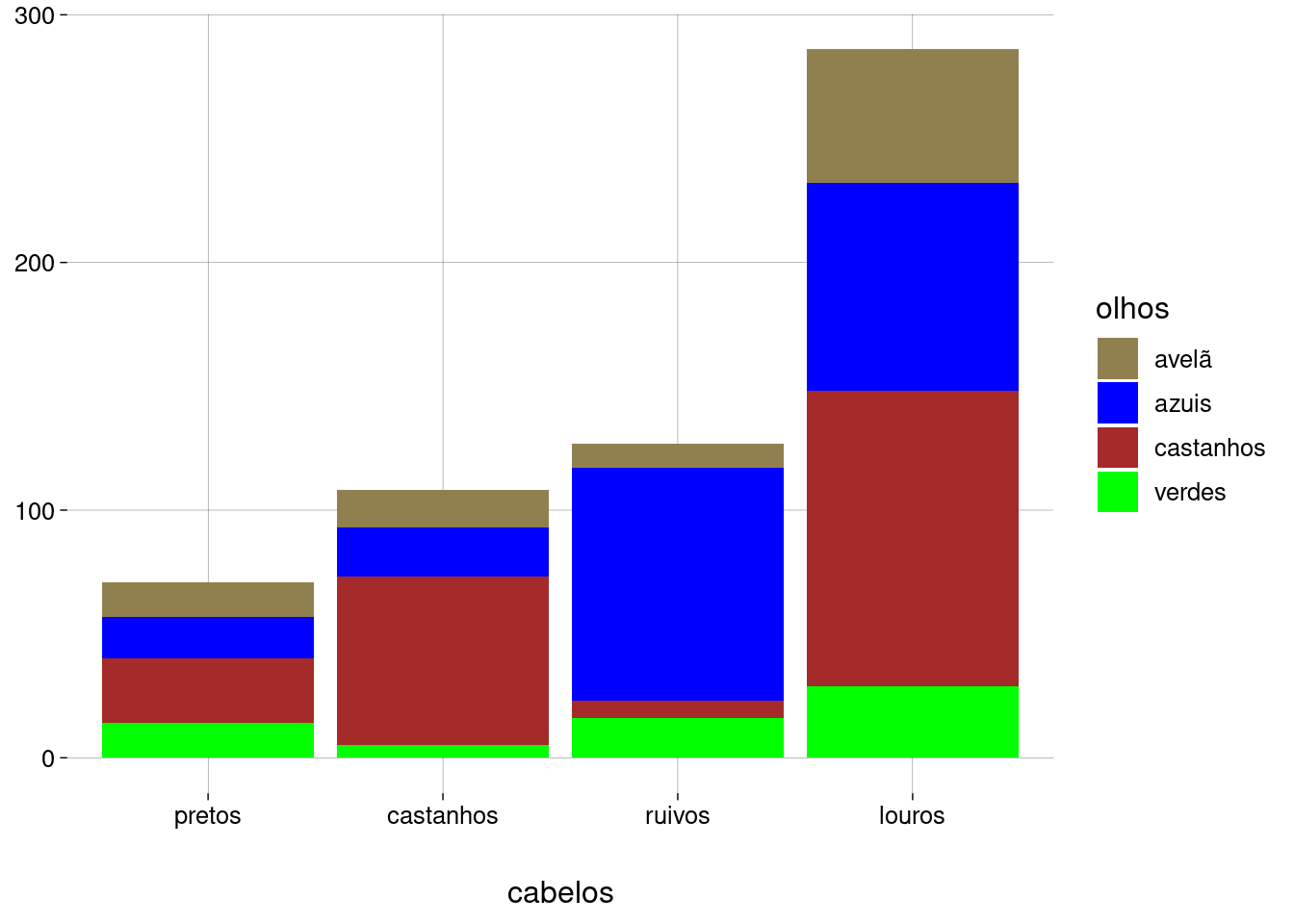
    )

Ou, com barras lado a lado:

df %>% 
  ggplot(aes(x = fct_rev(fct_infreq(cabelos)), fill = olhos)) +
    geom_bar(position = 'dodge') +
    scale_fill_discrete(
      type = c('#908050', 'blue', 'brown', 'green')
    ) +
    labs(
      x = 'cabelos',
      y = NULL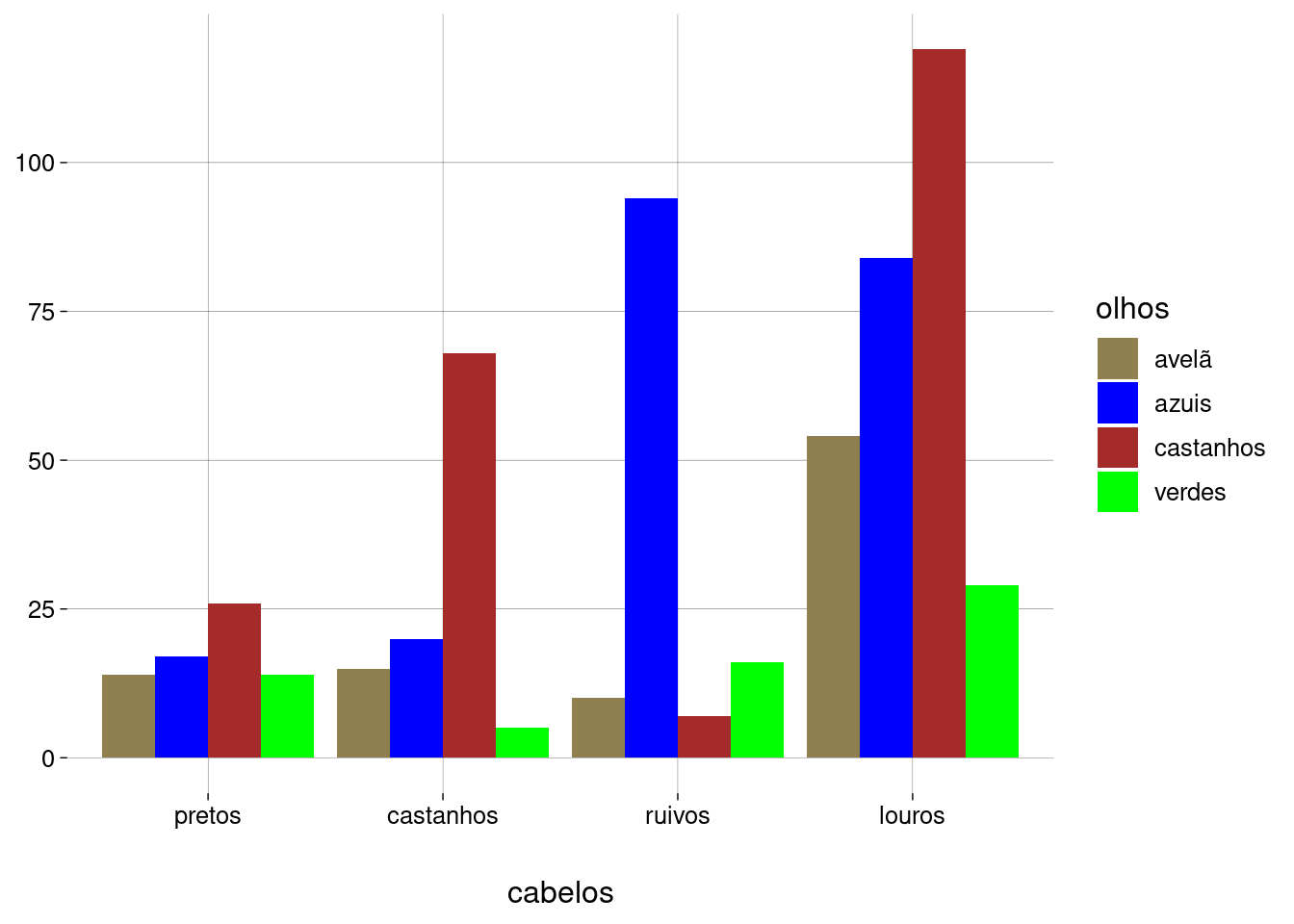
    )

Observações e perguntas:
1. Há mais pessoas louras de olhos castanhos do que louras de olhos azuis. O esperado não seria mais pessoas louras de olhos azuis? Pessoas louras de olhos castanhos pintaram os cabelos?
2. Há muito mais ruivos de olhos azuis do que ruivos de olhos verdes. Não deveria ser o contrário? Também são pessoas que pintaram os cabelos de ruivo? Ou houve erro no registro das cores dos olhos?

Para incluir o sexo, podemos facetar o gráfico. Usando facet_wrap³, geramos dois subgráficos lado a lado:

df %>% 
  ggplot(aes(x = fct_rev(fct_infreq(cabelos)), fill = olhos)) +
    geom_bar(position = 'dodge') +
    scale_fill_discrete(type = c('#908050', 'blue', 'brown', 'green')) +
    facet_wrap(~sexo) +
    labs(
      title = 'Cores de cabelos e olhos por sexo',
      y = NULL,
      x = 'cabelos'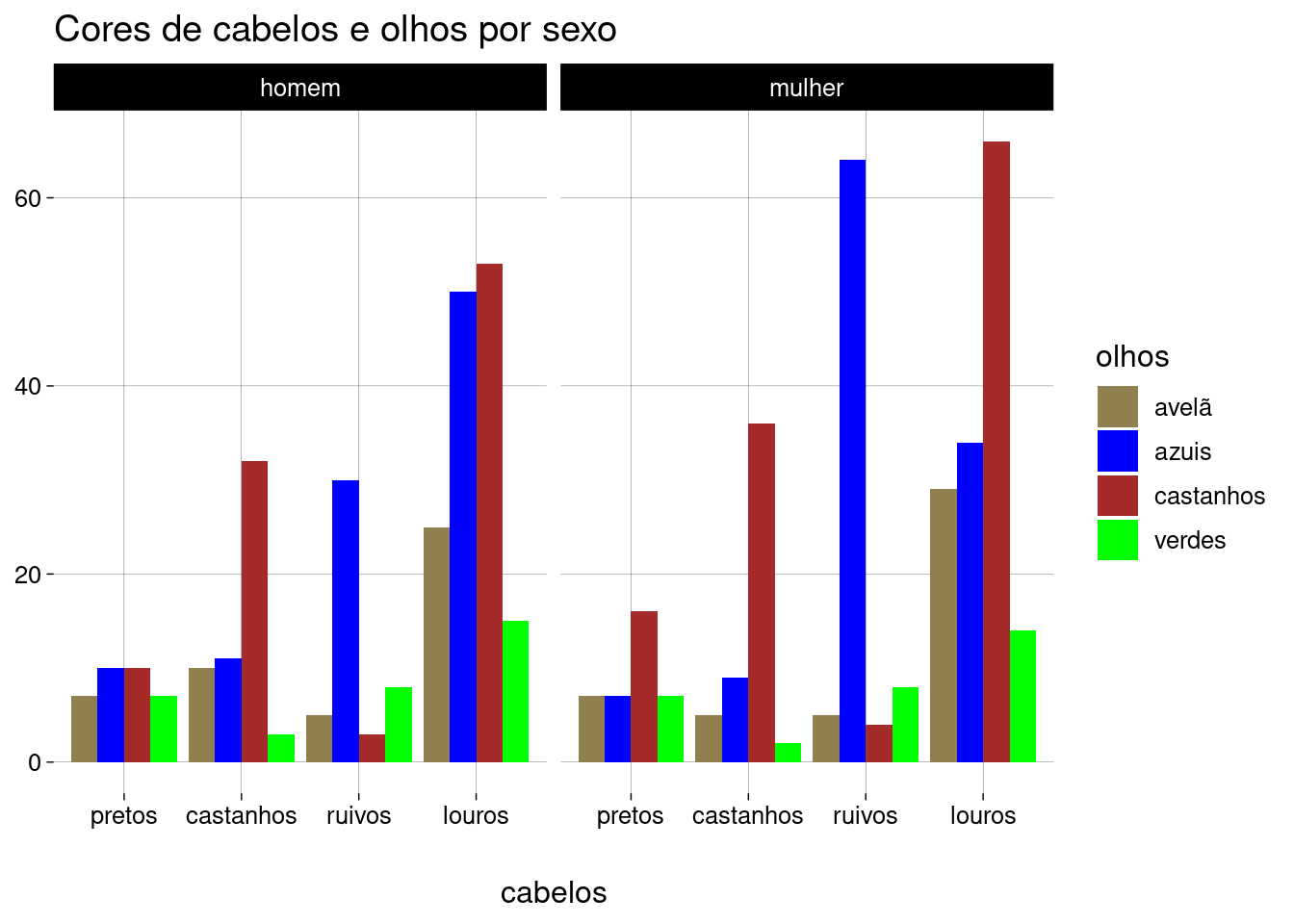
    )

Se a quantidade grande de pessoas louras de olhos castanhos (em comparação com pessoas louras de olhos azuis) for por causa da pintura de cabelos, então o gráfico acima mostra que as mulheres pintam os cabelos de louro com mais frequência do que os homens.

Quando facetamos por cor de cabelos, também podemos observar as mesmas diferenças entre homens e mulheres:

df %>% 
  ggplot(aes(x = sexo, fill = fct_infreq(olhos))) +
    geom_bar(position = 'dodge') +
    facet_wrap(~cabelos, labeller = label_both) +
    scale_fill_discrete(type = c('brown', 'blue', '#908050', 'green')) +
    labs(
      x = NULL,
      y = NULL,
      fill = 'olhos',
      title = 'Cor dos olhos e sexo por cor dos cabelos'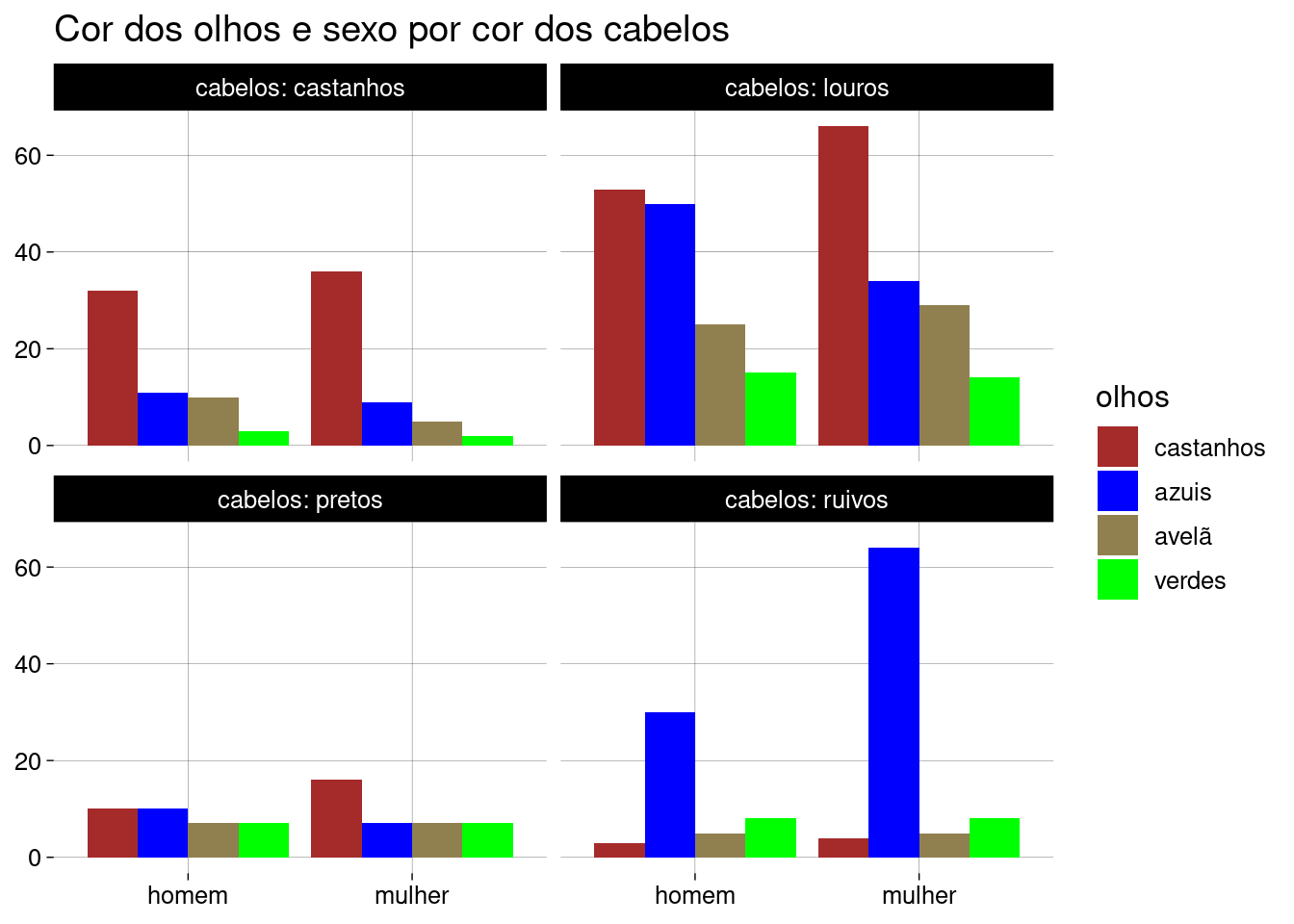
    )

5.4.3 Data frame já contendo os totais

Você percebeu que geom_bar analisa o data frame e calcula as frequências necessárias para construir o gráfico.
Em algumas situações, o data frame já contém as frequências (em vez de conter uma linha por indivíduo).
Vamos usar count para criar um data frame assim:
```
df_tot <- df %>% 
  count(sexo, cabelos, olhos)

df_tot
```
Para \(4\) cores de cabelo, \(4\) cores de olhos, e \(2\) sexos, são \(32\) combinações possíveis.

Com este data frame, podemos gerar todos os gráficos anteriores usando geom_col no lugar de geom_bar. Por exemplo: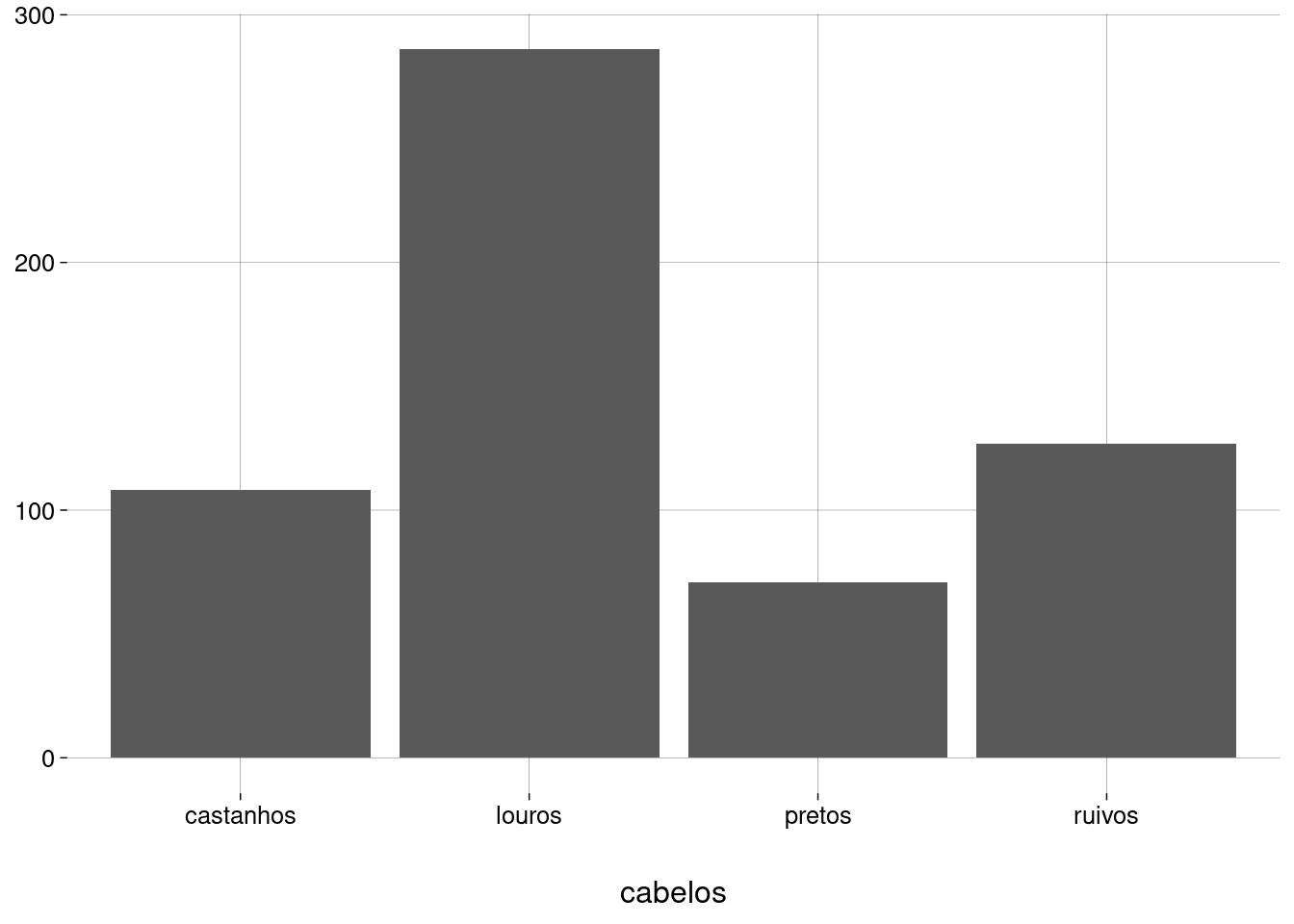

df_tot %>% 
  ggplot(aes(x = cabelos, y = n)) +
    geom_col() +
    labs(
      y = NULL
    )

Com geom_col, precisamos passar a estética \(y\) (no nosso exemplo, a variável n, que contém as frequências).
Para ordenar as barras, usamos a função fct_reorder, que ordena os níveis de um fator (cabelos) de acordo com o resultado de uma função (sum) aplicada sobre os valores de outra variável (n):
```
df_tot %>% 
  ggplot(aes(x = fct_reorder(cabelos, n, sum), y = n)) +
    geom_col() +
    labs(
      x = 'cabelos',
      y = NULL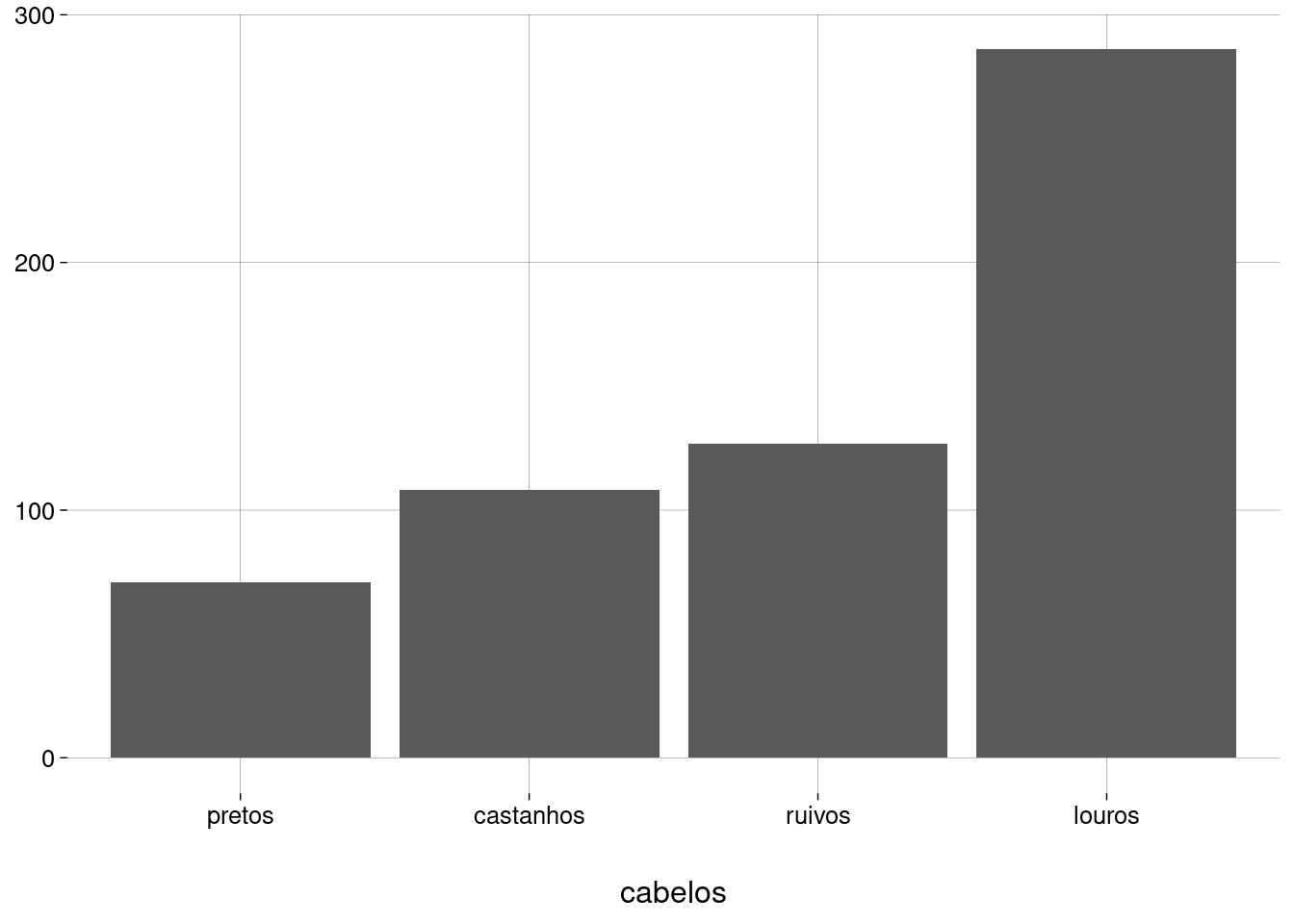
    )
```

5.5 Gráficos de linha e séries temporais

5.5.1 Conjunto de dados

O R tem uma matriz com as quantidades de telefones em várias regiões do mundo ao longo de vários anos:

WorldPhones

##      N.Amer Europe Asia S.Amer Oceania Africa Mid.Amer
## 1951  45939  21574 2876   1815    1646     89      555
## 1956  60423  29990 4708   2568    2366   1411      733
## 1957  64721  32510 5230   2695    2526   1546      773
## 1958  68484  35218 6662   2845    2691   1663      836
## 1959  71799  37598 6856   3000    2868   1769      911
## 1960  76036  40341 8220   3145    3054   1905     1008
## 1961  79831  43173 9053   3338    3224   2005     1076

Os números representam milhares.
Os números dos anos são os nomes das linhas da matriz.
Vamos transformar esta matriz em uma tibble:
```
fones <- WorldPhones %>% 
  as_tibble(rownames = 'Ano') %>% 
  mutate(Ano = as.numeric(Ano))

fones
```
Esta tibble não está no formato tidy. Queremos que cada linha corresponda a uma observação, contendo
- Ano,
- Região,
- Quantidade de telefones.
Usamos a função pivot_longer para mudar o formato da tibble:
```
fones_long <- fones %>% 
  pivot_longer(
    cols = -Ano,
    names_to = 'Região',
    values_to = 'n'
  )

fones_long
```
Confira: antes, tínhamos \(7\) anos, com \(7\) quantidades por ano, uma quantidade por região. Eram \(49\) quantidades. Agora temos uma tibble de \(49\) linhas.

5.5.2 Gerando gráficos de linha

A geometria geom_line gera gráficos de linha. Perceba como geramos uma linha por região:

fones_long %>% 
  ggplot(aes(x = Ano, y = n, color = Região)) +
    geom_line() +
    scale_x_continuous(breaks = 1951:1961)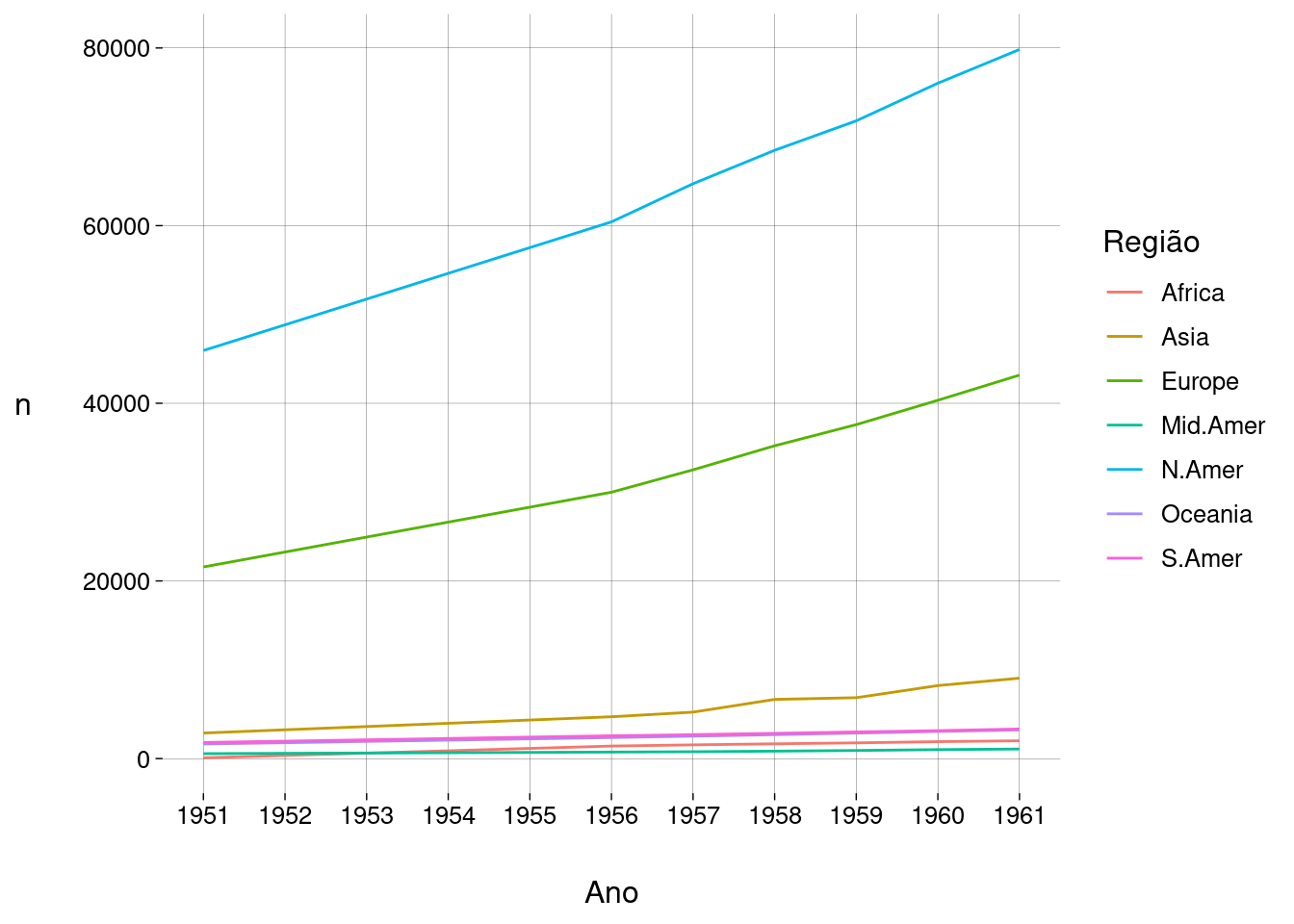

Embora a legenda associe uma cor a cada região, a leitura seria mais fácil se a ordem das regiões na legenda coincidisse com a posição das linhas na borda direita da grade:

fones_long %>% 
  ggplot(
      aes(
        x = Ano, 
        y = n, 
        color = fct_rev(fct_reorder(Região, n, max))
      )
  ) +
    geom_line() +
    scale_x_continuous(breaks = 1951:1961) +
    labs(
      color = 'Região',
      y = '',
      x = NULL,
      title = 'Quantidade de aparelhos de telefone por ano, por região'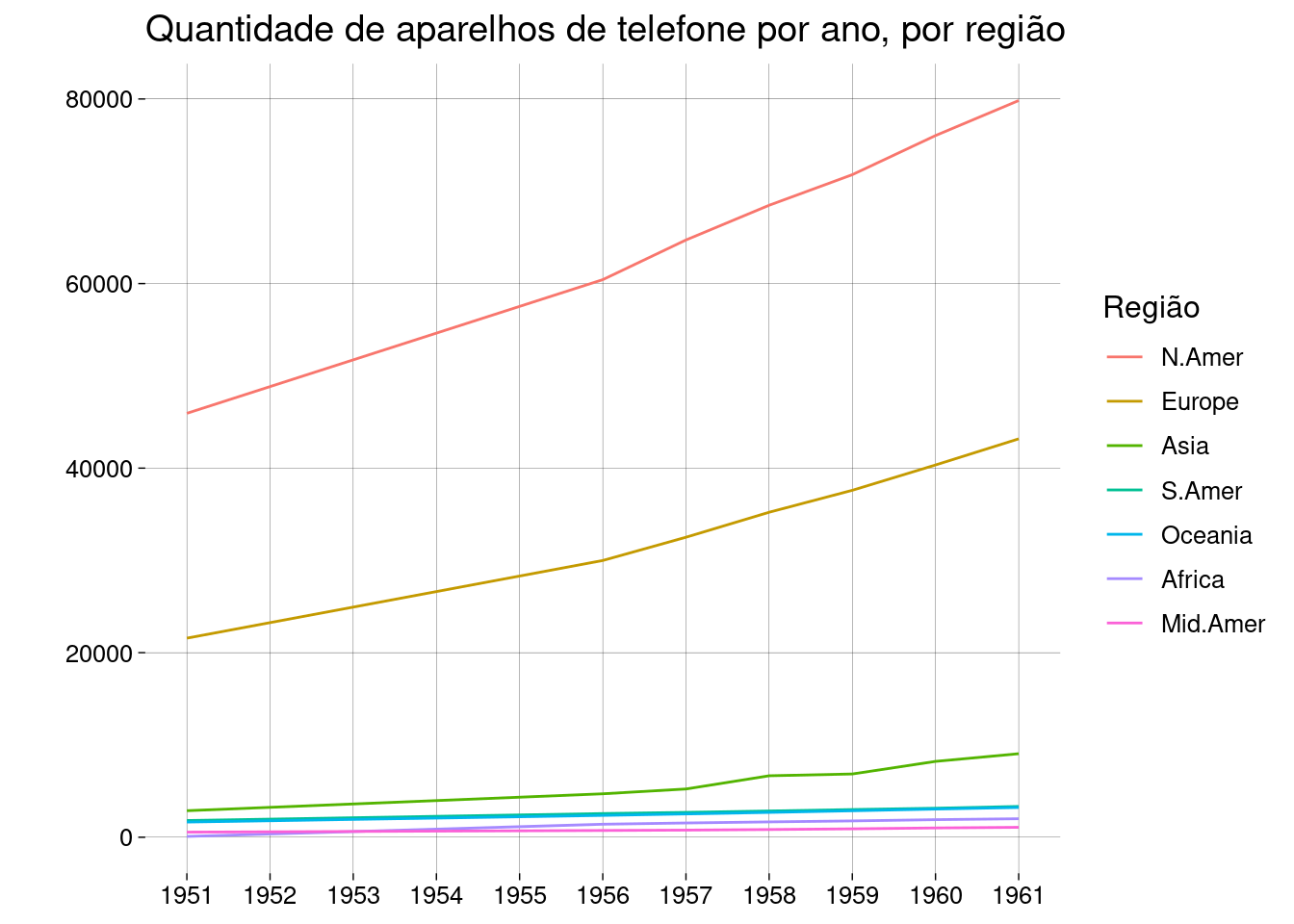
    )

Parece que está faltando uma linha, mas o que acontece é que as quantidades da América do Sul e da Oceania são bem parecidas:

fones_long %>%
  filter(Região %in% c('S.Amer', 'Oceania')) %>% 
  ggplot(
    aes(
      x = Ano, 
      y = n, 
      color = fct_rev(fct_reorder(Região, n, max))
    )
  ) +
    geom_line() +
    scale_x_continuous(breaks = 1951:1961) +
    labs(y = NULL, color = 'Região')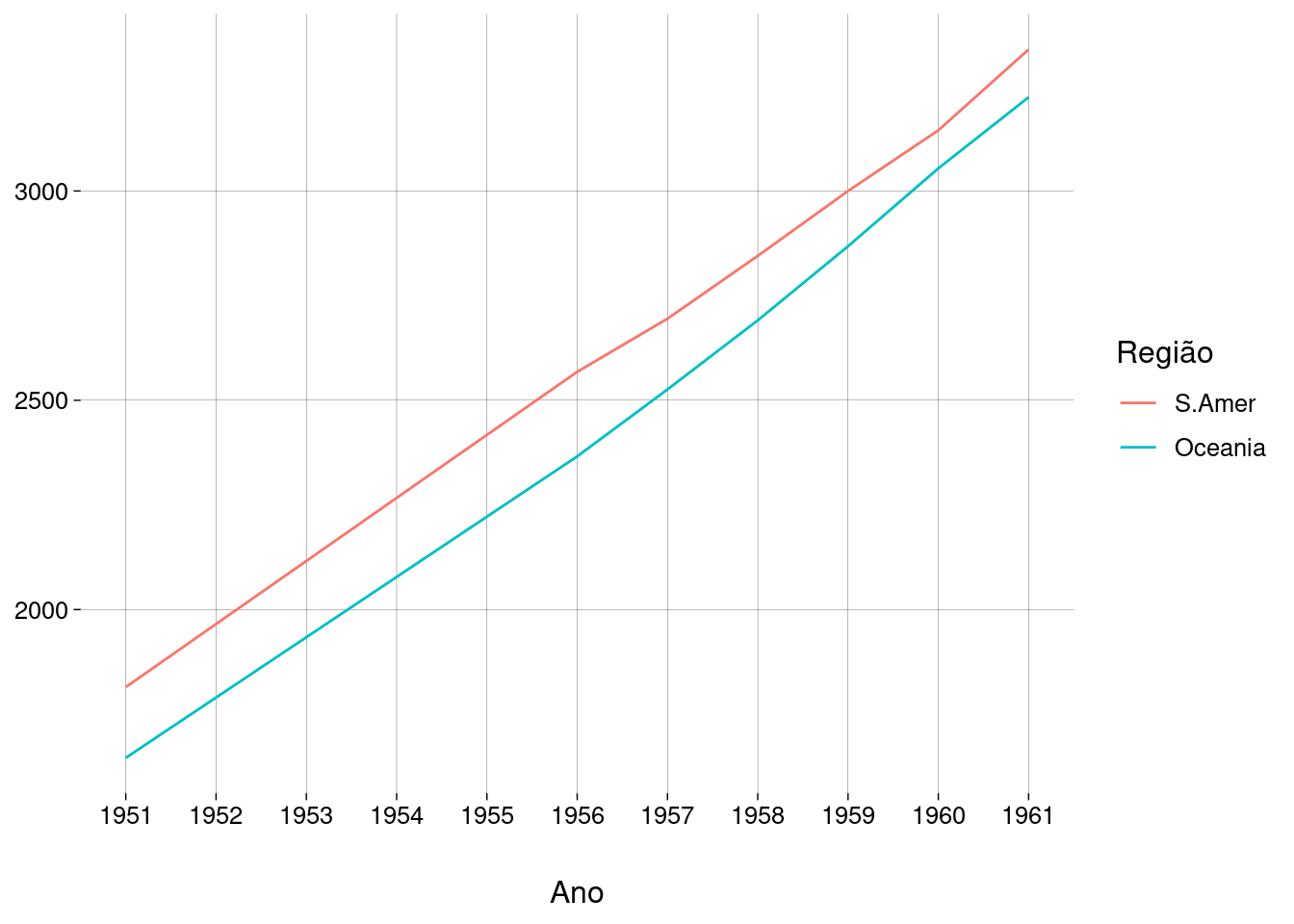

Estamos tratando estes dados como simples números, mas, na verdade, este conjunto de dados é uma série temporal (time series).
R tem todo um conjunto de funções para tratar séries temporais, calcular tendências, achar padrões cíclicos, fazer estimativas, e gerar gráficos específicos, entre outras coisas.
Mas não vamos falar mais sobre séries temporais aqui.
O pacote tsibble oferece maneiras de trabalhar com séries temporais de maneira tidy. Você pode ler a documentação do pacote entrando
```
library(tsibble)
?`tsibble-package`
```

5.6 Exercícios

5.6.1 O bigode dos onívoros

Examine o data frame sono para descobrir o que houve com o bigode superior do boxplot dos onívoros neste gráfico.

5.6.2 Usando `geom_col`

Use geom_col para reproduzir, a partir do data frame df_tot, todos os gráficos que foram gerados com geom_bar na seção Gerando gráficos de barras.

5.7 Referências sobre visualização e R