Capítulo 4 Visualização com ggplot2

Busque mais informações sobre os pacotes tidyverse e ggplot2 nas referências recomendadas.

4.1 Vídeo 1

4.2 Componentes de um gráfico ggplot2

4.2.1 Geometrias e mapeamentos estéticos (mappings)

Observe o gráfico abaixo, obtido de https://www.gapminder.org/downloads/updated-gapminder-world-poster-2015/.

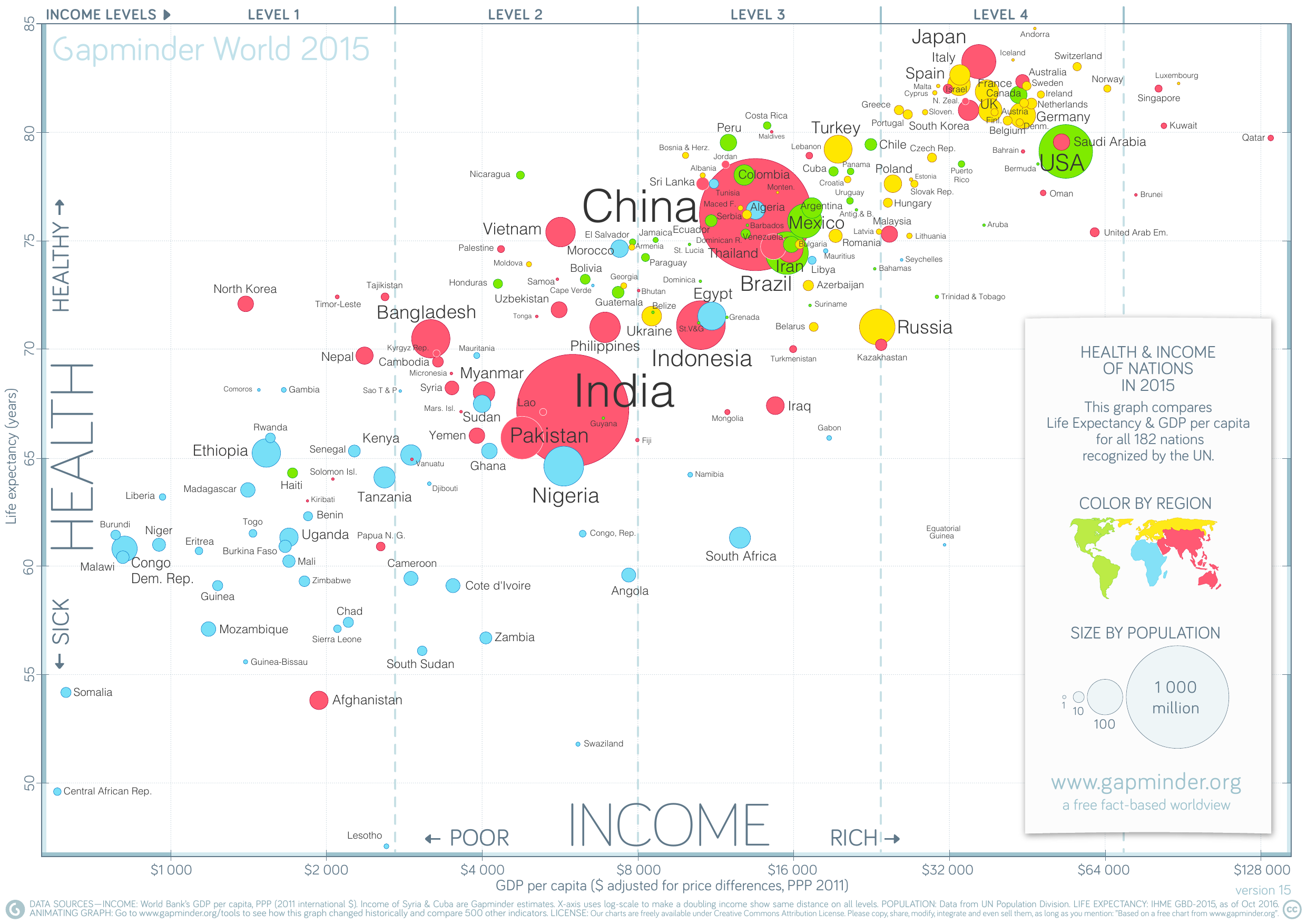
O gráfico mostra como, em cada país, a saúde (mais precisamente, a expectativa de vida) se relaciona com a riqueza (mais precisamente, o PIB per capita).
Além da expectativa de vida e o do PIB per capita, o gráfico traz mais informações sobre cada país.
Cada país é representado por um ponto (a geometria).
Informações sobre cada país são representadas por características do ponto correspondente (as estéticas):

Variável Geometria Estética

PIB per capita ponto posição x

Expectativa de vida ponto posição y

População ponto tamanho

Continente ponto cor
Você pode usar outras estéticas para representar informações:
- Cor de preenchimento.
- Cor do traço.
- Tipo do traço (sólido, pontilhado, tracejado etc.).
- Forma (círculo, quadrado, triângulo etc.).
- Opacidade.
- etc.
Você pode usar outras geometrias:
- Linhas.
- Barras ou colunas.
- Caixas.
- etc.

Variável	Geometria	Estética
PIB per capita	ponto	posição x
Expectativa de vida	ponto	posição y
População	ponto	tamanho
Continente	ponto	cor

4.2.2 Escalas (scales)

As escalas controlam os detalhes da aparência da geometria e do mapeamento (eixos, cores etc.).
Os eixos do gráfico acima são escalas contínuas, com valores reais.
Observe o eixo horizontal. Os valores não aumentam linearmente, mas sim exponencialmente: cada passo à direita equivale a dobrar o valor do PIB. O eixo horizontal segue uma escala logarítmica.
Os tamanhos dos pontos formam uma escala discreta, com $4$ valores possíveis (veja a legenda no canto inferior direito do gráfico).
As cores também formam uma escala discreta.

4.2.3 Rótulos (labels)

O gráfico também representa informação na forma de texto.
Além de rótulos (por exemplo, o texto que identifica cada eixo), o texto também pode, ele mesmo, ser uma geometria, com suas próprias estéticas: observe como o nome de cada país é escrito em um tamanho proporcional à sua população.

4.2.4 Outros componentes

Coordenadas:
- Este gráfico usa coordenadas cartesianas, com eixos $x$ e $y$.
- Existem gráficos que usam um sistema de coordenadas polares.
Temas:
- Incluem todos os elementos “decorativos”: cor de fundo, linhas de grade, etc. Ajudam a facilitar a leitura e a interpretação.
- No gráfico acima, um detalhe interessante do tema é a divisão de cada eixo em segmentos claros e segmentos escuros.
Legendas (guides).
Facetas:
- Às vezes, um gráfico é composto por múltiplos subgráficos.
- Cada subgráfico é uma faceta.
- Facetas evitam que informações demais sejam apresentadas no mesmo lugar.

4.3 Conjunto de dados

Nossos exemplos de gráficos vão usar dados sobre o sono de diversos mamíferos.
O conjunto de dados se chama msleep e está incluído no pacote ggplot2.
Para ver a documentação, digite
```
library(ggplot2)
?msleep
```
Vamos atribuir o conjunto de dados à variável df:
```
df <- msleep
df
```

Vamos examinar a estrutura — usando R base:

str(df)

## tibble [83 × 11] (S3: tbl_df/tbl/data.frame)
##  $ name        : chr [1:83] "Cheetah" "Owl monkey" "Mountain beaver" ...
##  $ genus       : chr [1:83] "Acinonyx" "Aotus" "Aplodontia" ...
##  $ vore        : chr [1:83] "carni" "omni" "herbi" ...
##  $ order       : chr [1:83] "Carnivora" "Primates" "Rodentia" ...
##  $ conservation: chr [1:83] "lc" NA "nt" ...
##  $ sleep_total : num [1:83] 12,1 17 14,4 14,9 4 14,4 8,7 7 ...
##  $ sleep_rem   : num [1:83] NA 1,8 2,4 2,3 0,7 2,2 1,4 NA ...
##  $ sleep_cycle : num [1:83] NA NA NA 0,133 ...
##  $ awake       : num [1:83] 11,9 7 9,6 9,1 20 9,6 15,3 17 ...
##  $ brainwt     : num [1:83] NA 0,0155 NA 0,00029 0,423 NA NA NA ...
##  $ bodywt      : num [1:83] 50 0,48 1,35 0,019 ...

Podemos usar glimpse, uma função do tidyverse:

glimpse(df)

## Rows: 83
## Columns: 11
## $ name         <chr> "Cheetah", "Owl monkey", "Mountain beaver", "Greater short-tai…
## $ genus        <chr> "Acinonyx", "Aotus", "Aplodontia", "Blarina", "Bos", "Bradypus…
## $ vore         <chr> "carni", "omni", "herbi", "omni", "herbi", "herbi", "carni", N…
## $ order        <chr> "Carnivora", "Primates", "Rodentia", "Soricomorpha", "Artiodac…
## $ conservation <chr> "lc", NA, "nt", "lc", "domesticated", NA, "vu", NA, "domestica…
## $ sleep_total  <dbl> 12,1, 17,0, 14,4, 14,9, 4,0, 14,4, 8,7, 7,0, 10,1, 3,0, 5,3, 9…
## $ sleep_rem    <dbl> NA, 1,8, 2,4, 2,3, 0,7, 2,2, 1,4, NA, 2,9, NA, 0,6, 0,8, 0,7, …
## $ sleep_cycle  <dbl> NA, NA, NA, 0,1333333, 0,6666667, 0,7666667, 0,3833333, NA, 0,…
## $ awake        <dbl> 11,9, 7,0, 9,6, 9,1, 20,0, 9,6, 15,3, 17,0, 13,9, 21,0, 18,7, …
## $ brainwt      <dbl> NA, 0,01550, NA, 0,00029, 0,42300, NA, NA, NA, 0,07000, 0,0982…
## $ bodywt       <dbl> 50,000, 0,480, 1,350, 0,019, 600,000, 3,850, 20,490, 0,045, 14…

Para examinar só as primeiras linhas do data frame:
```
head(df)
```
Para examinar o data frame interativamente:
```
view(df)
```

Podemos produzir um sumário dos dados usando o pacote summarytools (que já foi carregado neste documento):

df %>% dfSummary() %>% print()

Variável	Estatísticas / Valores	Freqs (% de Válidos)	Faltante
name [character]	1. African elephant 2. African giant pouched rat 3. African striped mouse 4. Arctic fox 5. Arctic ground squirrel 6. Asian elephant 7. Baboon 8. Big brown bat 9. Bottle-nosed dolphin 10. Brazilian tapir [ 73 outros ]	1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 73 (88,0%)	0 (0,0%)
genus [character]	1. Panthera 2. Spermophilus 3. Equus 4. Vulpes 5. Acinonyx 6. Aotus 7. Aplodontia 8. Blarina 9. Bos 10. Bradypus [ 67 outros ]	3 ( 3,6%) 3 ( 3,6%) 2 ( 2,4%) 2 ( 2,4%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 67 (80,7%)	0 (0,0%)
vore [character]	1. carni 2. herbi 3. insecti 4. omni	19 (25,0%) 32 (42,1%) 5 ( 6,6%) 20 (26,3%)	7 (8,4%)
order [character]	1. Rodentia 2. Carnivora 3. Primates 4. Artiodactyla 5. Soricomorpha 6. Cetacea 7. Hyracoidea 8. Perissodactyla 9. Chiroptera 10. Cingulata [ 9 outros ]	22 (26,5%) 12 (14,5%) 12 (14,5%) 6 ( 7,2%) 5 ( 6,0%) 3 ( 3,6%) 3 ( 3,6%) 3 ( 3,6%) 2 ( 2,4%) 2 ( 2,4%) 13 (15,7%)	0 (0,0%)
conservation [character]	1. cd 2. domesticated 3. en 4. lc 5. nt 6. vu	2 ( 3,7%) 10 (18,5%) 4 ( 7,4%) 27 (50,0%) 4 ( 7,4%) 7 (13,0%)	29 (34,9%)
sleep_total [numeric]	Média (dp) : 10,4 (4,5) mín < mediana < máx: 1,9 < 10,1 < 19,9 IQE (CV) : 5,9 (0,4)	65 valores distintos	0 (0,0%)
sleep_rem [numeric]	Média (dp) : 1,9 (1,3) mín < mediana < máx: 0,1 < 1,5 < 6,6 IQE (CV) : 1,5 (0,7)	32 valores distintos	22 (26,5%)
sleep_cycle [numeric]	Média (dp) : 0,4 (0,4) mín < mediana < máx: 0,1 < 0,3 < 1,5 IQE (CV) : 0,4 (0,8)	22 valores distintos	51 (61,4%)
awake [numeric]	Média (dp) : 13,6 (4,5) mín < mediana < máx: 4,1 < 13,9 < 22,1 IQE (CV) : 5,9 (0,3)	65 valores distintos	0 (0,0%)
brainwt [numeric]	Média (dp) : 0,3 (1) mín < mediana < máx: 0 < 0 < 5,7 IQE (CV) : 0,1 (3,5)	53 valores distintos	27 (32,5%)
bodywt [numeric]	Média (dp) : 166,1 (786,8) mín < mediana < máx: 0 < 1,7 < 6654 IQE (CV) : 41,6 (4,7)	82 valores distintos	0 (0,0%)

Vemos que há muitos NA em diversas variáveis. Para nossos exemplos simples de visualização, vamos usar as colunas
- name
- genus
- order
- sleep_total
- awake
- bodywt
- brainwt
Mas… a coluna que mostra a dieta (vore) tem só 7 NA. Quais são?
```
df %>% 
  filter(is.na(vore)) %>% 
  select(name)
```
OK. Vamos manter a coluna vore também, apesar dos NA. Quando formos usar esta variável, tomaremos cuidado.
Também… a coluna bodywt tem 0 como valor mínimo. Como assim?
```
df %>% 
  filter(bodywt < 1) %>% 
  select(name, bodywt) %>% 
  arrange(bodywt)
```
Ah, sem problema. A função dfSummary arredondou estes pesos para 0. Os valores de verdade ainda estão na tibble.

Vamos criar uma tibble nova, só com as colunas que nos interessam:

sono <- df %>% 
  select(
    name, order, genus, vore, bodywt, 
    brainwt, awake, sleep_total
  )

Vamos ver o sumário:

sono %>% dfSummary() %>% print()

Variável	Estatísticas / Valores	Freqs (% de Válidos)	Faltante
name [character]	1. African elephant 2. African giant pouched rat 3. African striped mouse 4. Arctic fox 5. Arctic ground squirrel 6. Asian elephant 7. Baboon 8. Big brown bat 9. Bottle-nosed dolphin 10. Brazilian tapir [ 73 outros ]	1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 73 (88,0%)	0 (0,0%)
order [character]	1. Rodentia 2. Carnivora 3. Primates 4. Artiodactyla 5. Soricomorpha 6. Cetacea 7. Hyracoidea 8. Perissodactyla 9. Chiroptera 10. Cingulata [ 9 outros ]	22 (26,5%) 12 (14,5%) 12 (14,5%) 6 ( 7,2%) 5 ( 6,0%) 3 ( 3,6%) 3 ( 3,6%) 3 ( 3,6%) 2 ( 2,4%) 2 ( 2,4%) 13 (15,7%)	0 (0,0%)
genus [character]	1. Panthera 2. Spermophilus 3. Equus 4. Vulpes 5. Acinonyx 6. Aotus 7. Aplodontia 8. Blarina 9. Bos 10. Bradypus [ 67 outros ]	3 ( 3,6%) 3 ( 3,6%) 2 ( 2,4%) 2 ( 2,4%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 1 ( 1,2%) 67 (80,7%)	0 (0,0%)
vore [character]	1. carni 2. herbi 3. insecti 4. omni	19 (25,0%) 32 (42,1%) 5 ( 6,6%) 20 (26,3%)	7 (8,4%)
bodywt [numeric]	Média (dp) : 166,1 (786,8) mín < mediana < máx: 0 < 1,7 < 6654 IQE (CV) : 41,6 (4,7)	82 valores distintos	0 (0,0%)
brainwt [numeric]	Média (dp) : 0,3 (1) mín < mediana < máx: 0 < 0 < 5,7 IQE (CV) : 0,1 (3,5)	53 valores distintos	27 (32,5%)
awake [numeric]	Média (dp) : 13,6 (4,5) mín < mediana < máx: 4,1 < 13,9 < 22,1 IQE (CV) : 5,9 (0,3)	65 valores distintos	0 (0,0%)
sleep_total [numeric]	Média (dp) : 10,4 (4,5) mín < mediana < máx: 1,9 < 10,1 < 19,9 IQE (CV) : 5,9 (0,4)	65 valores distintos	0 (0,0%)

4.4 Gráficos de dispersão (scatter plots)

Servem para visualizar a relação entre duas variáveis quantitativas.
Essa relação não é necessariamente de causa e efeito.
Isto é, a variável do eixo horizontal não determina, necessariamente, os valores da variável do eixo vertical.
Pense em associação, correlação, não em causalidade.
Troque as variáveis de eixo, se ajudar a deixar isto claro.

4.4.1 Horas de sono e peso corporal

Como as variáveis sleep_total e bodywt estão relacionadas?

sono %>% 
  ggplot(aes(x = bodywt, y = sleep_total))

O que houve? Cadê os pontos?
O problema foi que só especificamos o mapeamento estético (com aes, que são as iniciais de aesthetics). Faltou a geometria.
```
sono %>% 
  ggplot(aes(x = bodywt, y = sleep_total)) +
  geom_point()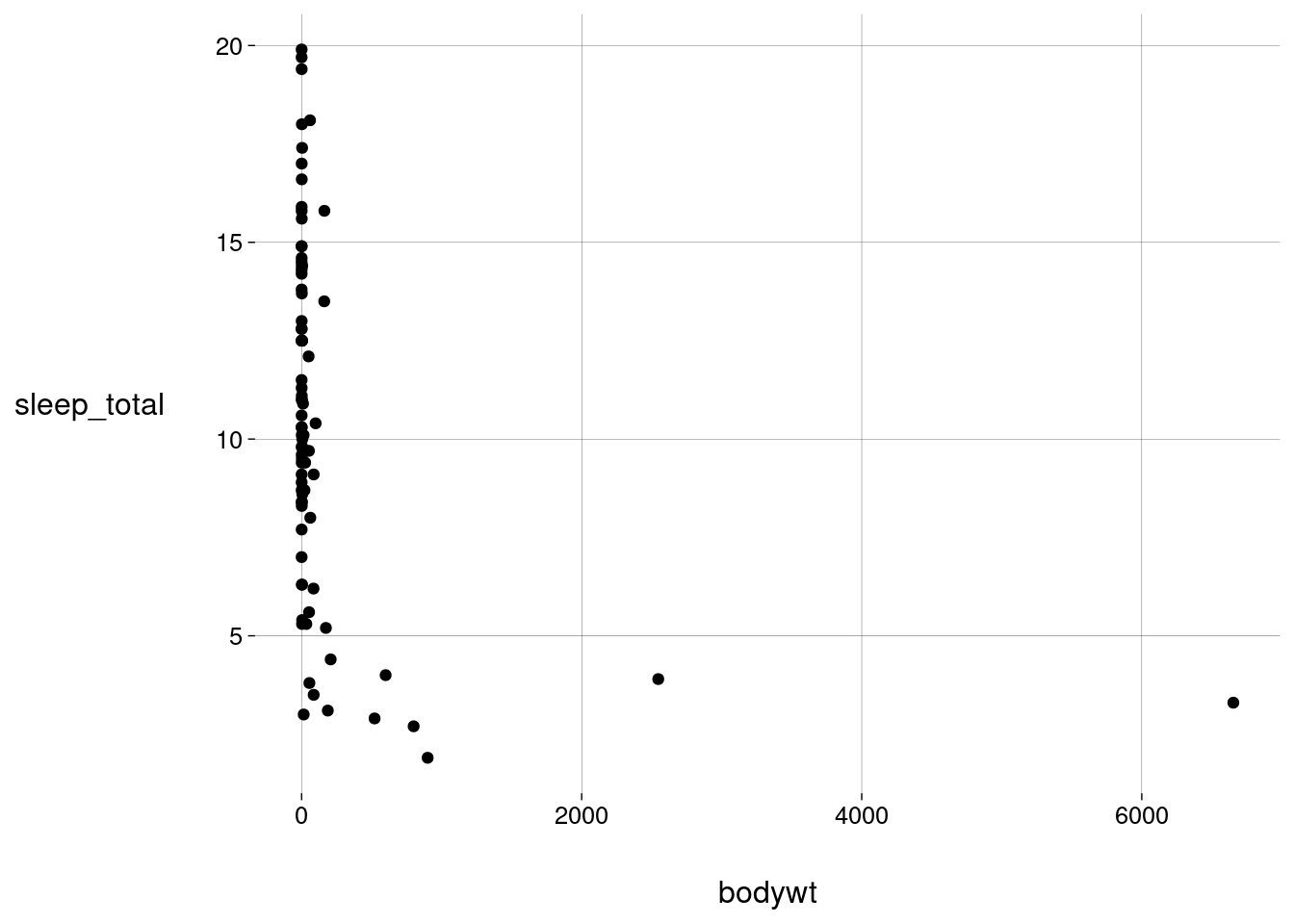
```
Que horror.
A única coisa que percebemos aqui é que os mamíferos muito pesados dormem menos de $5$ horas por noite.
Estes animais muito pesados estão estragando a escala do eixo $x$.
Que animais são estes?
```
sono %>% 
  filter(bodywt > 250) %>% 
  select(name, bodywt) %>% 
  arrange(bodywt)
```
Além disso, há muitos pontos sobrepostos. Em bom português, temos um problema de overplotting.
Existem diversas maneiras de lidar com isso.
A primeira delas é alterando a opacidade dos pontos. Isto é um ajuste na geometria apenas, pois a opacidade, aqui, não representa informação nenhuma.
```
sono %>% 
  ggplot(aes(x = bodywt, y = sleep_total)) +
    geom_point(alpha = 0.2)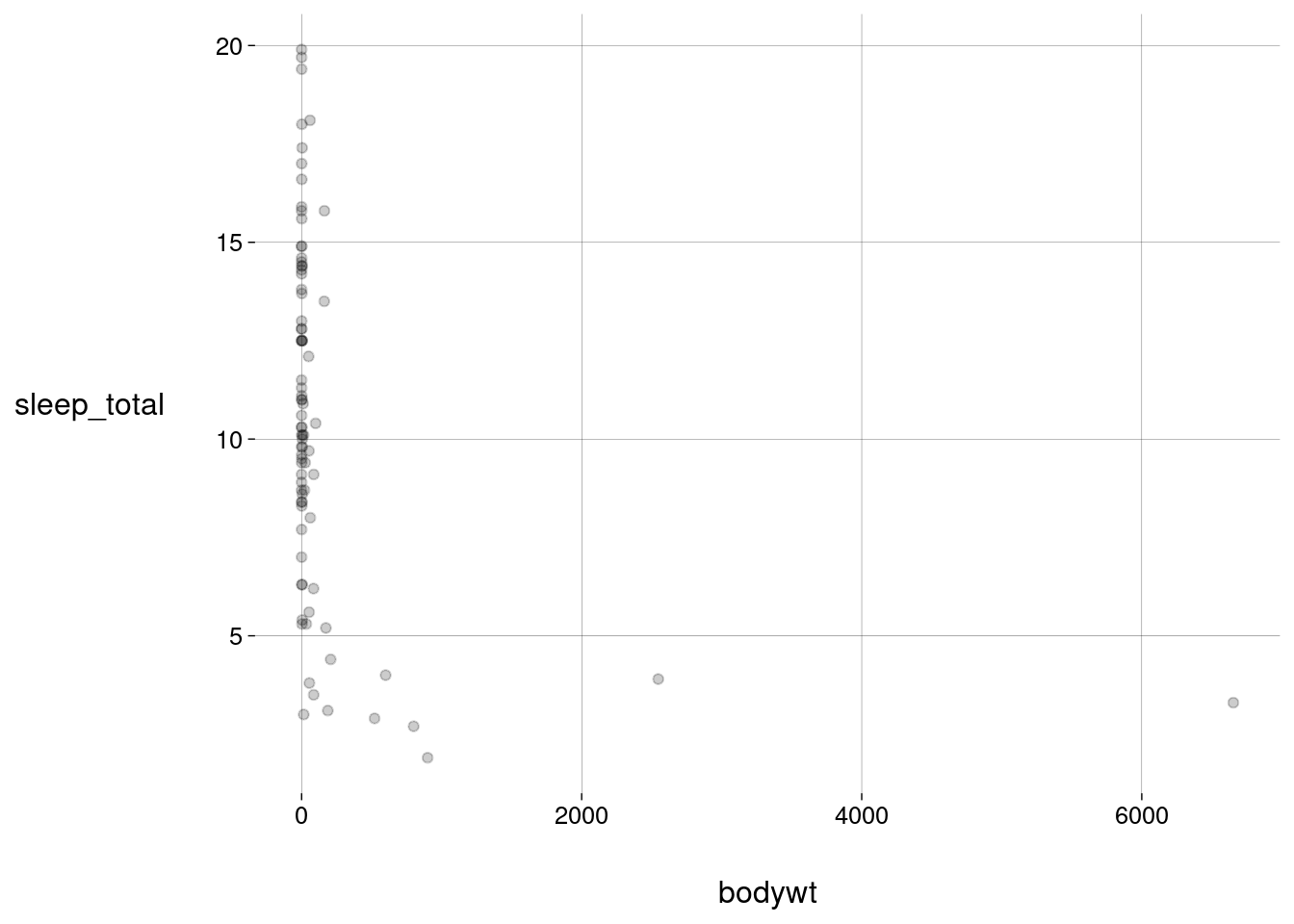
```
Outra maneira é usar geom_jitter em vez de geom_point. “Jitter” significa “tremer”. As posições dos pontos são ligeiramente perturbadas, para evitar colisões. Perdemos precisão, mas a visualização fica melhor.
```
sono %>% 
  ggplot(aes(x = bodywt, y = sleep_total)) +
    geom_jitter(width = 100)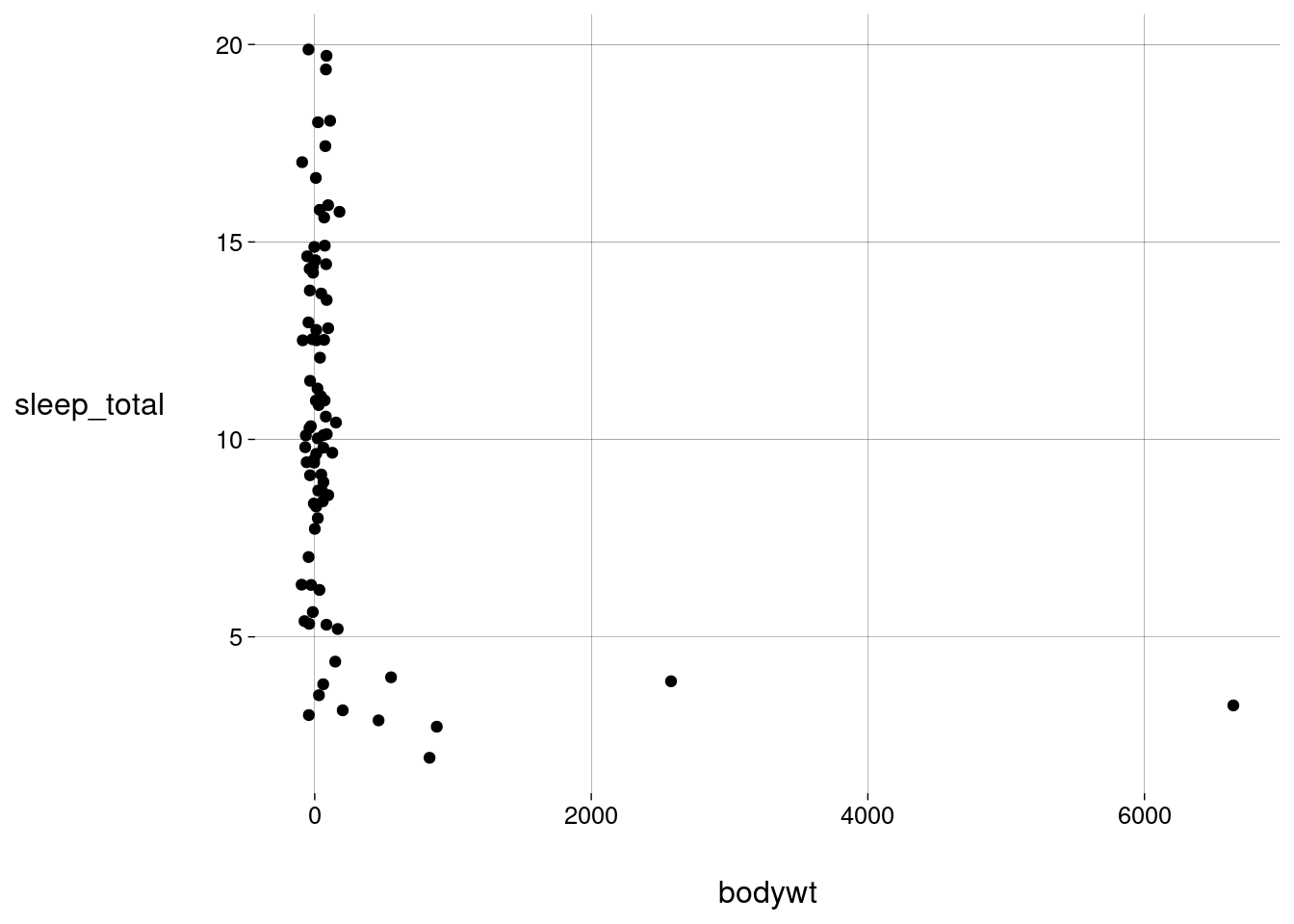
```

Vamos mudar os limites do gráfico para nos concentrarmos nos animais menos pesados. Observe que isto é um ajuste na escala.

sono %>% 
  ggplot(aes(x = bodywt, y = sleep_total)) +
    geom_point() +
    scale_x_continuous(limits = c(0, 200))

## Warning: Removed 7 rows containing missing values or values outside the scale range
## (`geom_point()`).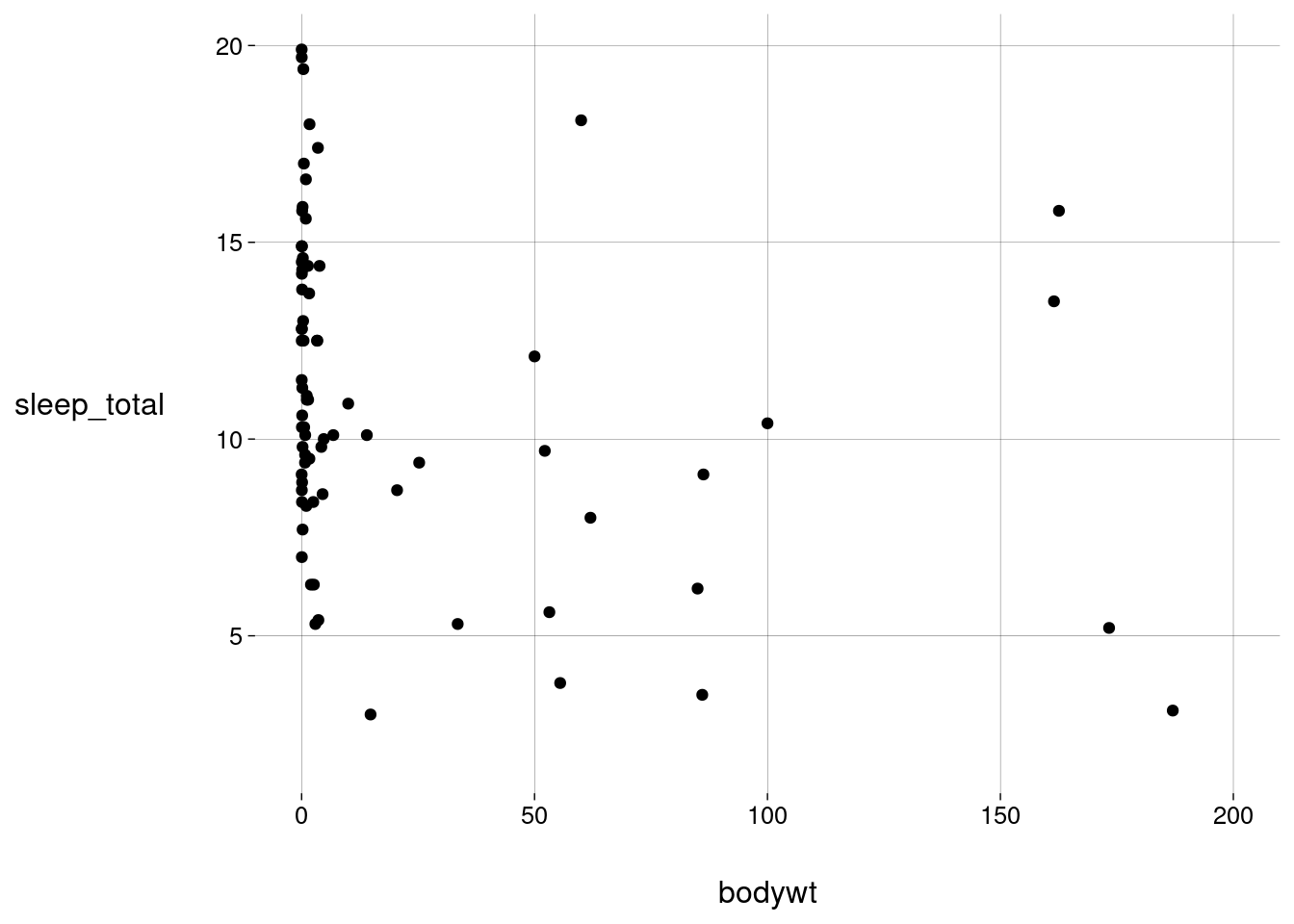

Nestes limites, a relação entre horas de sono e peso não é mais tão pronunciada.

4.4.2 Horas de sono e peso corporal para animais pequenos

Vamos restringir o gráfico a animais com no máximo $5$kg.
```
limite <- 5
```

Em vez de mudar a escala do gráfico, vamos filtrar as linhas do data frame:

sono %>% 
  filter(bodywt < limite) %>% 
  ggplot(aes(x = bodywt, y = sleep_total)) +
    geom_point()

4.4.3 Incluindo a dieta

Com a estética color. Observe como a legenda aparece automaticamente.

sono %>% 
  filter(bodywt < limite) %>% 
  ggplot(aes(x = bodywt, y = sleep_total, color = vore)) +
    geom_point()

4.4.4 A estética pode ser especificada na `geom`

Compare com o código anterior.

sono %>% 
  filter(bodywt < limite) %>% 
  ggplot() +
    geom_point(aes(x = bodywt, y = sleep_total, color = vore))

Fazendo deste modo, a estética só vale para uma geometria. Se você acrescentar outras geometrias (linhas, por exemplo), a estética não valerá para elas.

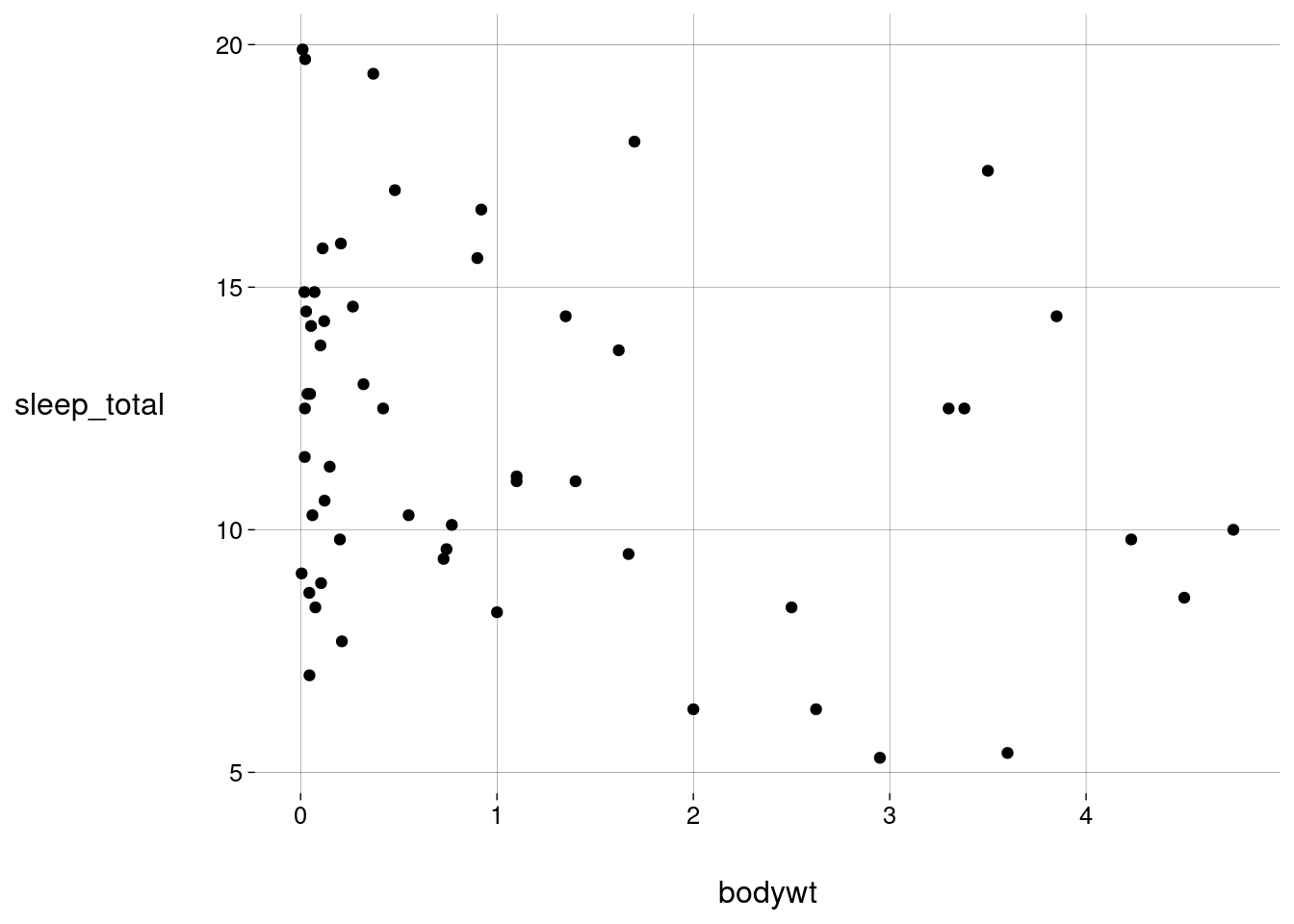
4.4.5 Aparência fixa ou dependendo de variável?

Se for fixa, não é estética. Não representa informação.
Se depender de variável, é estética. Representa informação.

Compare o último chunk acima com:

sono %>% 
  filter(bodywt < limite) %>% 
  ggplot() +
    geom_point(aes(x = bodywt, y = sleep_total), color = 'blue')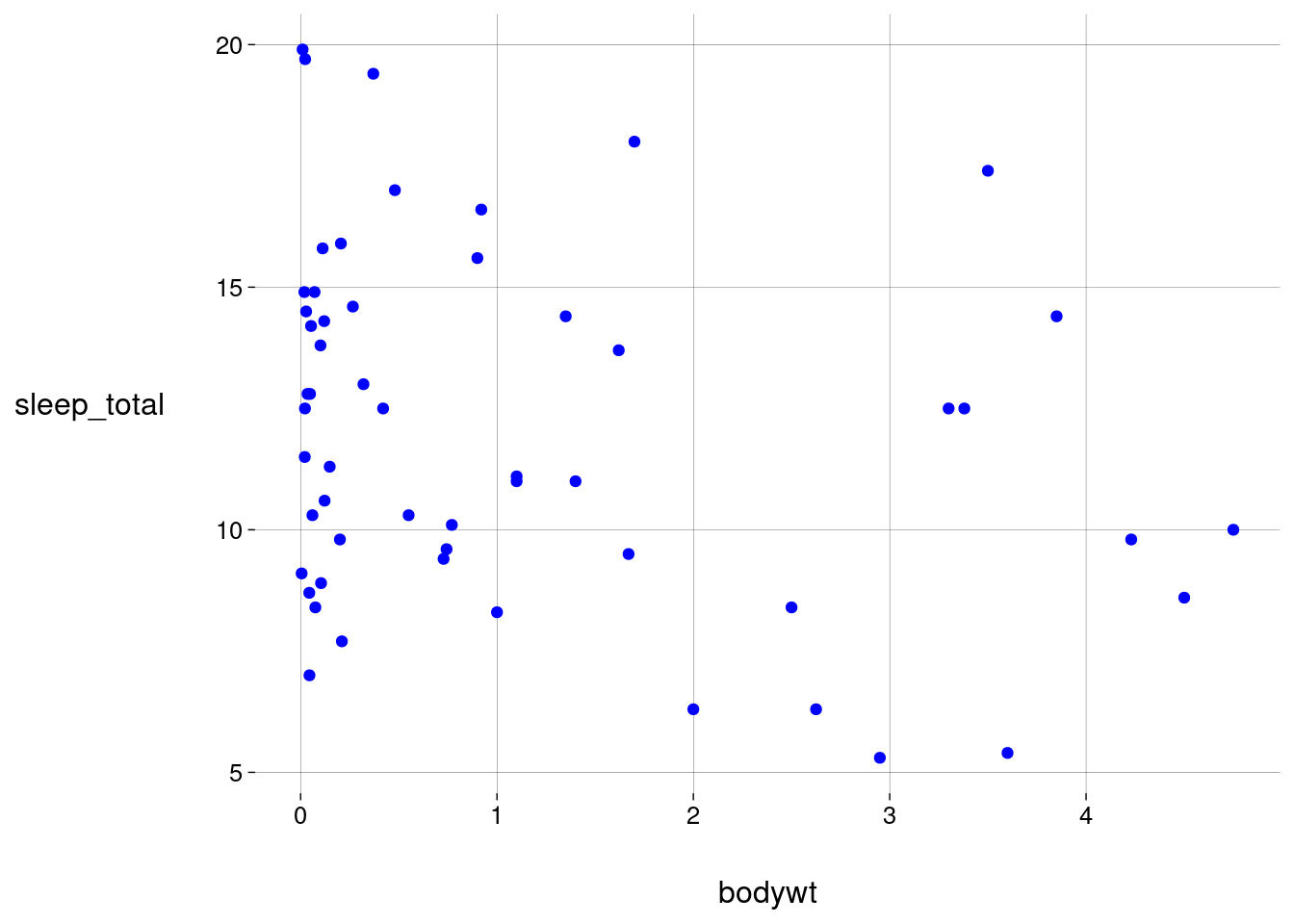

Se for uma estética, precisa estar associada a uma variável, não a um valor fixo. Um erro comum seria fazer:

sono %>% 
  filter(bodywt < limite) %>% 
  ggplot() +
    geom_point(aes(x = bodywt, y = sleep_total, color = 'blue'))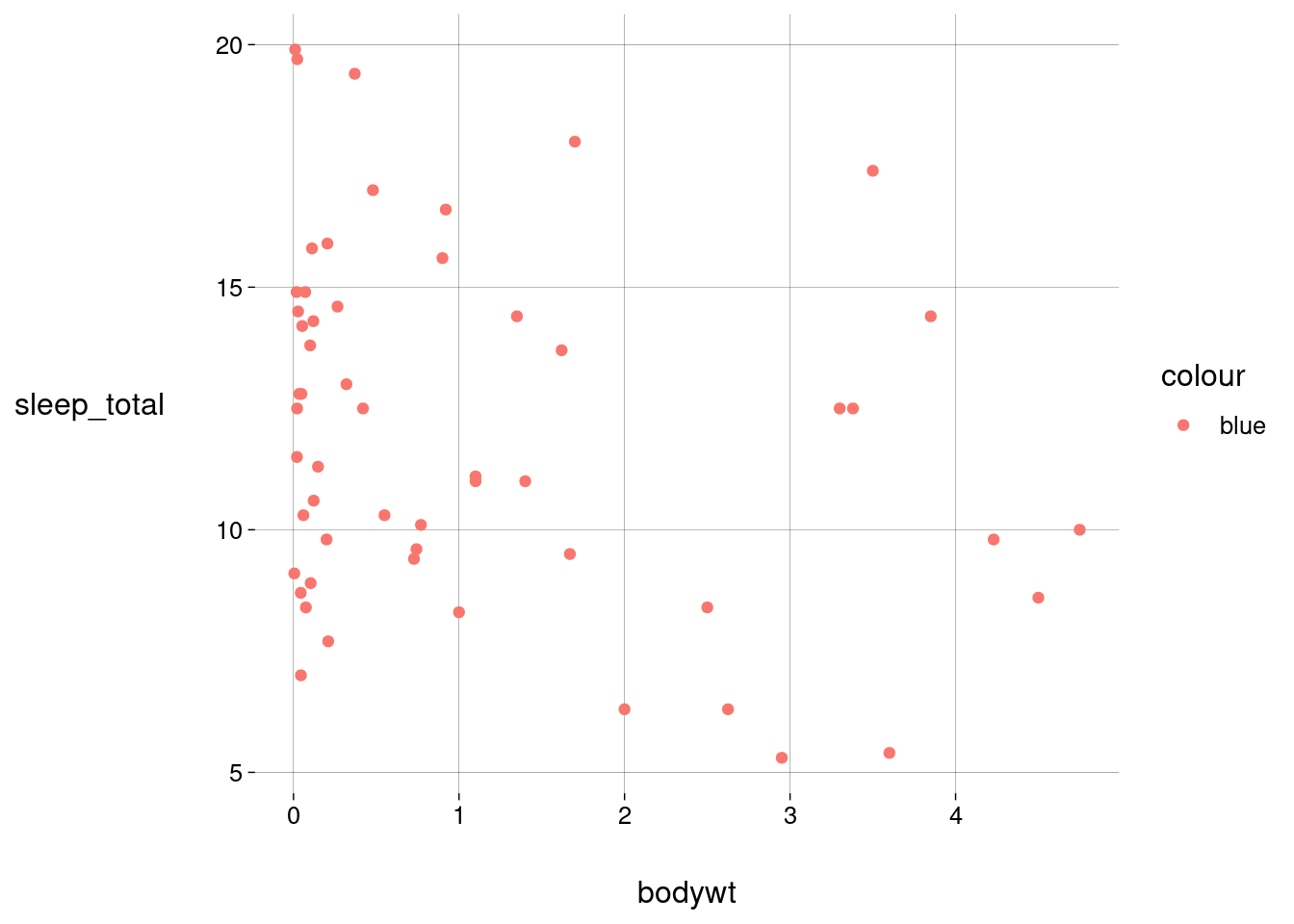

4.4.6 Uma correlação mais clara

Peso cerebral versus peso corporal:

sono %>% 
  ggplot(aes(x = bodywt, y = brainwt)) +
    geom_point()

## Warning: Removed 27 rows containing missing values or values outside the scale range
## (`geom_point()`).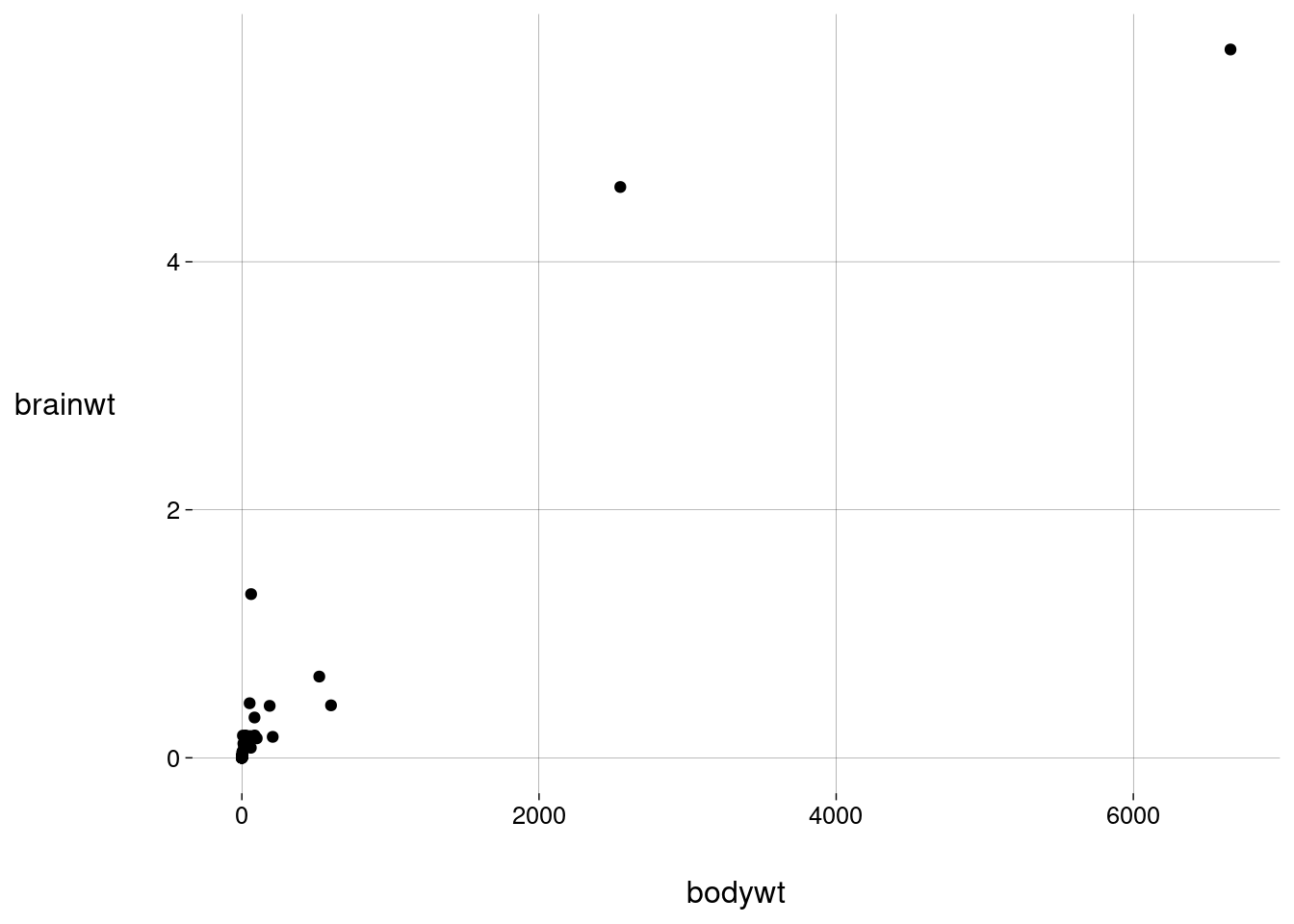

A mensagem de aviso (warning) diz que há $27$ valores faltantes (NA) em bodywt ou brainwt. De fato:
```
sono %>% 
  filter(is.na(bodywt)) %>% 
  count()
```
```
sono %>% 
  filter(is.na(brainwt)) %>% 
  count()
```

Vamos restringir aos animais mais leves e mudar a opacidade:

sono %>% 
  filter(bodywt < limite) %>% 
  ggplot(aes(x = bodywt, y = brainwt)) +
    geom_point(alpha = .5)

## Warning: Removed 18 rows containing missing values or values outside the scale range
## (`geom_point()`).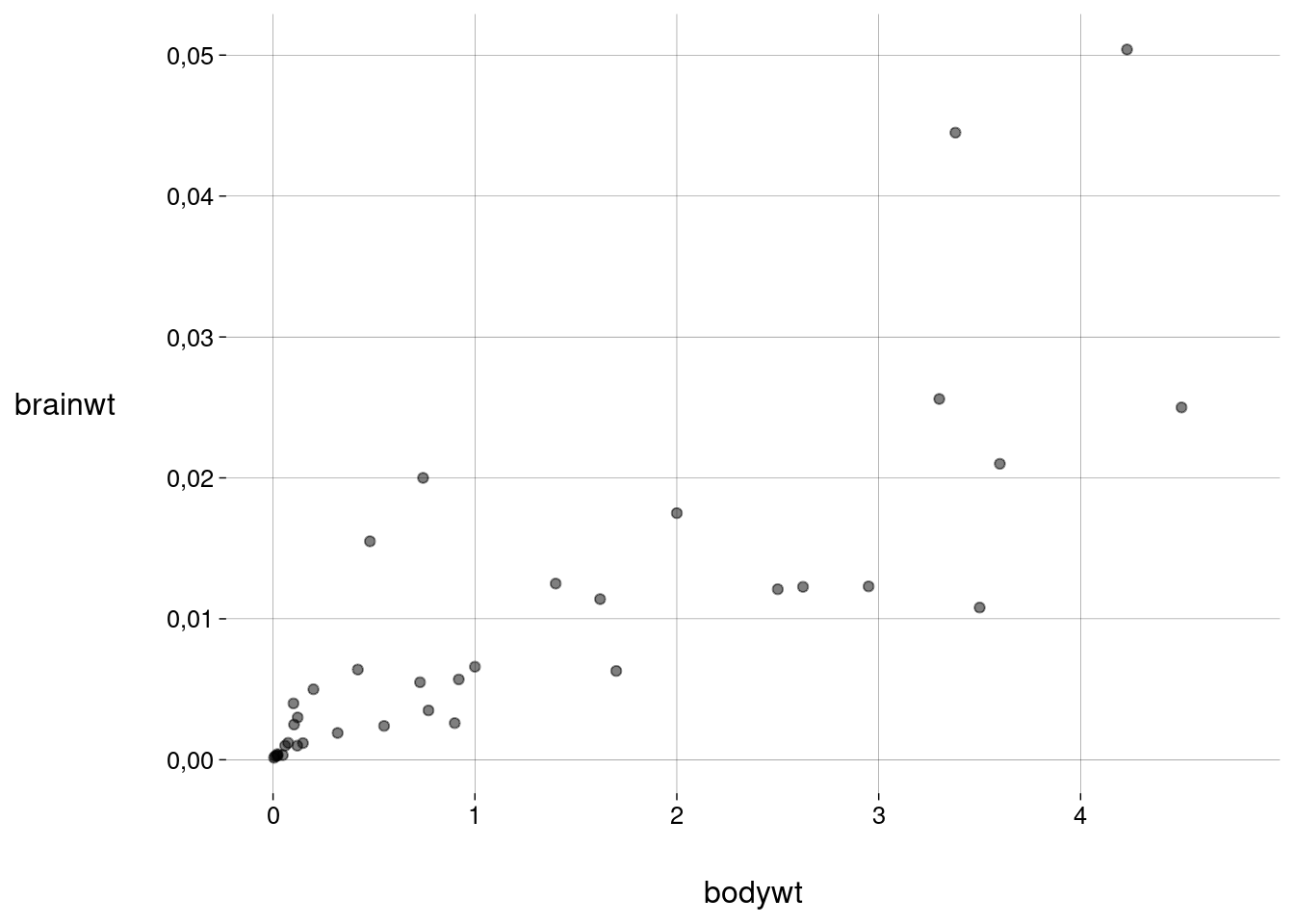

Vamos incluir horas de sono e dieta. Observe as estéticas usadas.

sono %>% 
  filter(bodywt < limite) %>% 
  ggplot(
    aes(
      x = bodywt, 
      y = brainwt,
      size = sleep_total,
      color = vore
    )
  ) +
    geom_point(alpha = .5)

## Warning: Removed 18 rows containing missing values or values outside the scale range
## (`geom_point()`).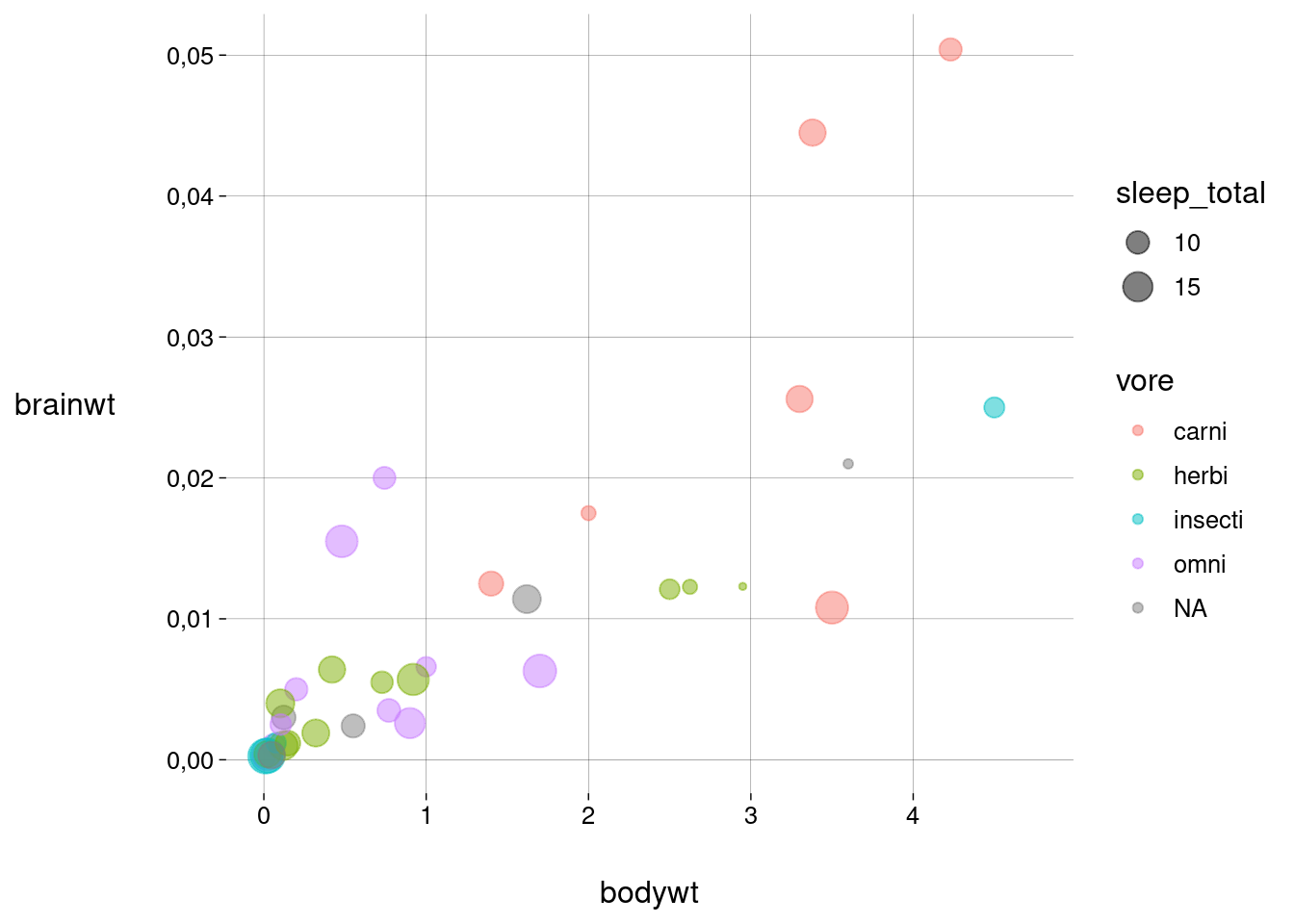

Vamos mudar a escala dos tamanhos e incluir rótulos:

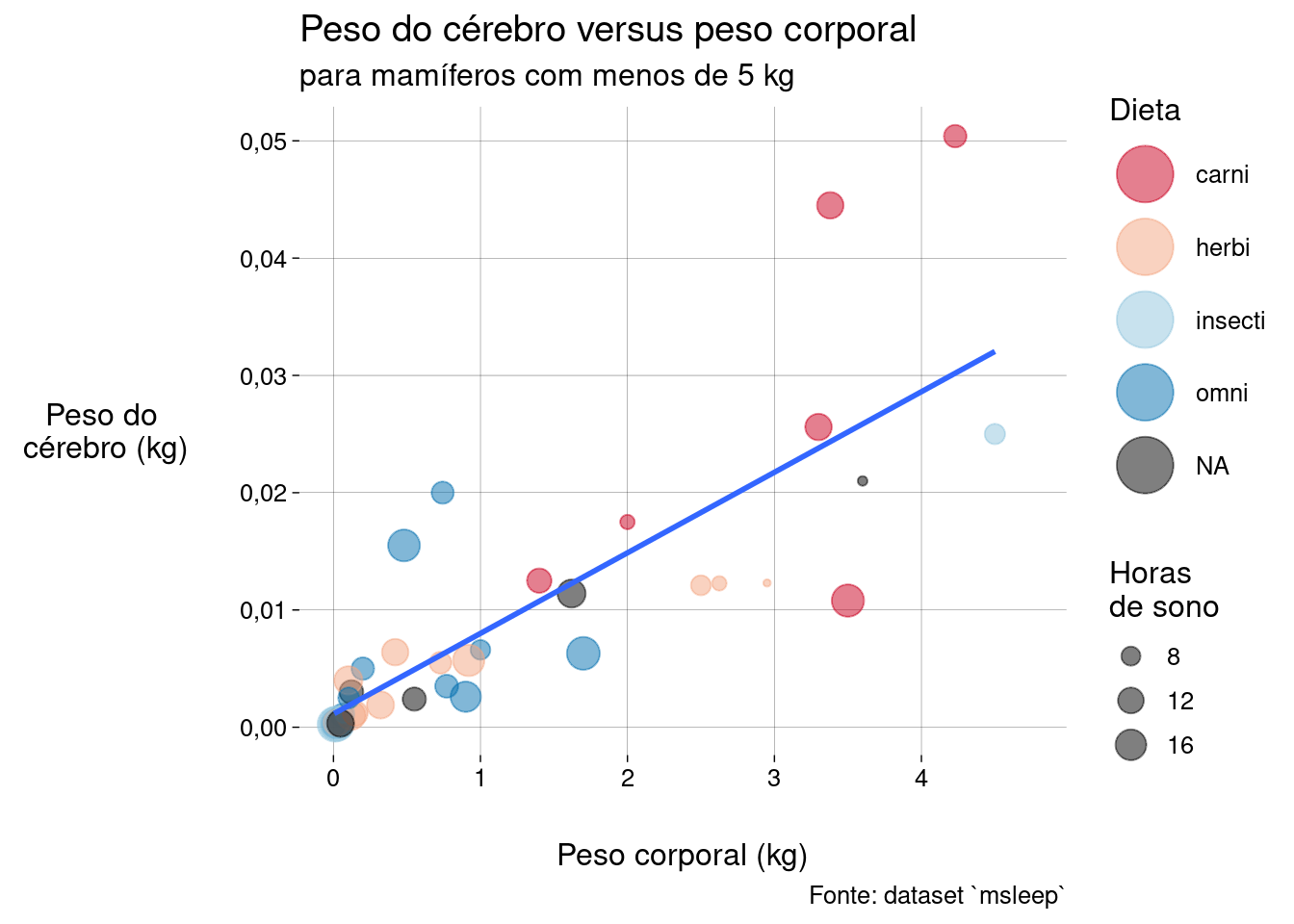
grafico <- sono %>% 
  filter(bodywt < limite) %>% 
  ggplot(
    aes(
      x = bodywt, 
      y = brainwt,
      size = sleep_total,
      color = vore
    )
  ) +
    geom_point(alpha = .5) +
    scale_size(
      breaks = seq(0, 24, 4)
    ) +
    labs(
      title = 'Peso do cérebro versus peso corporal',
      subtitle = paste0(
        'para mamíferos com menos de ', 
        limite, 
        ' kg'
      ),
      caption = 'Fonte: dataset `msleep`',
      x = 'Peso corporal (kg)',
      y = 'Peso do\n cérebro (kg)',
      color = 'Dieta',
      size = 'Horas\nde sono'
    )

grafico

## Warning: Removed 18 rows containing missing values or values outside the scale range
## (`geom_point()`).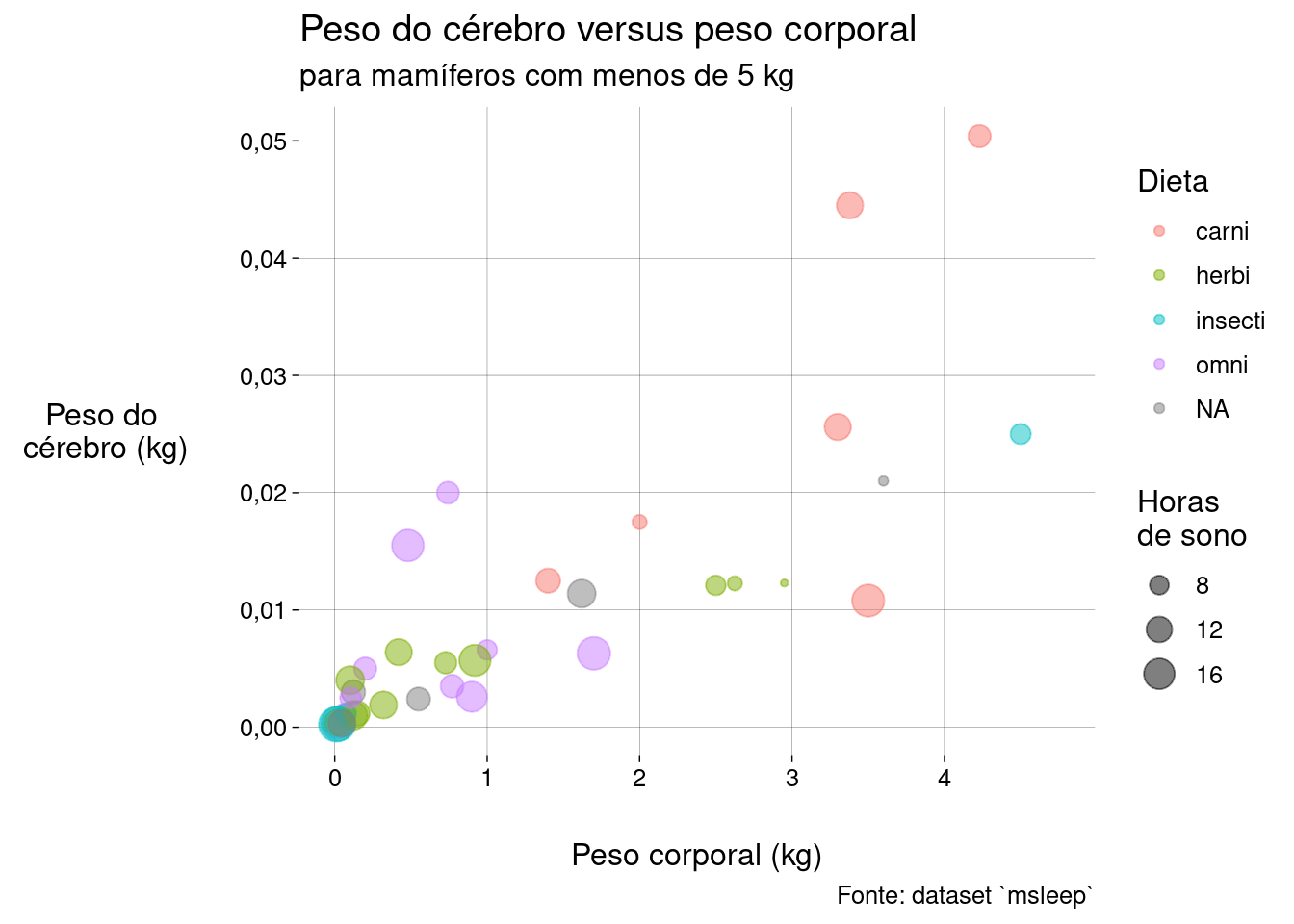

Vamos mudar as cores usadas para a dieta, usando uma escala diferente.

grafico2 <- grafico +
  scale_color_discrete(
    palette = 'RdBu',
    na.value = 'black',
    type = scale_color_brewer
  )

grafico2

## Warning: Removed 18 rows containing missing values or values outside the scale range
## (`geom_point()`).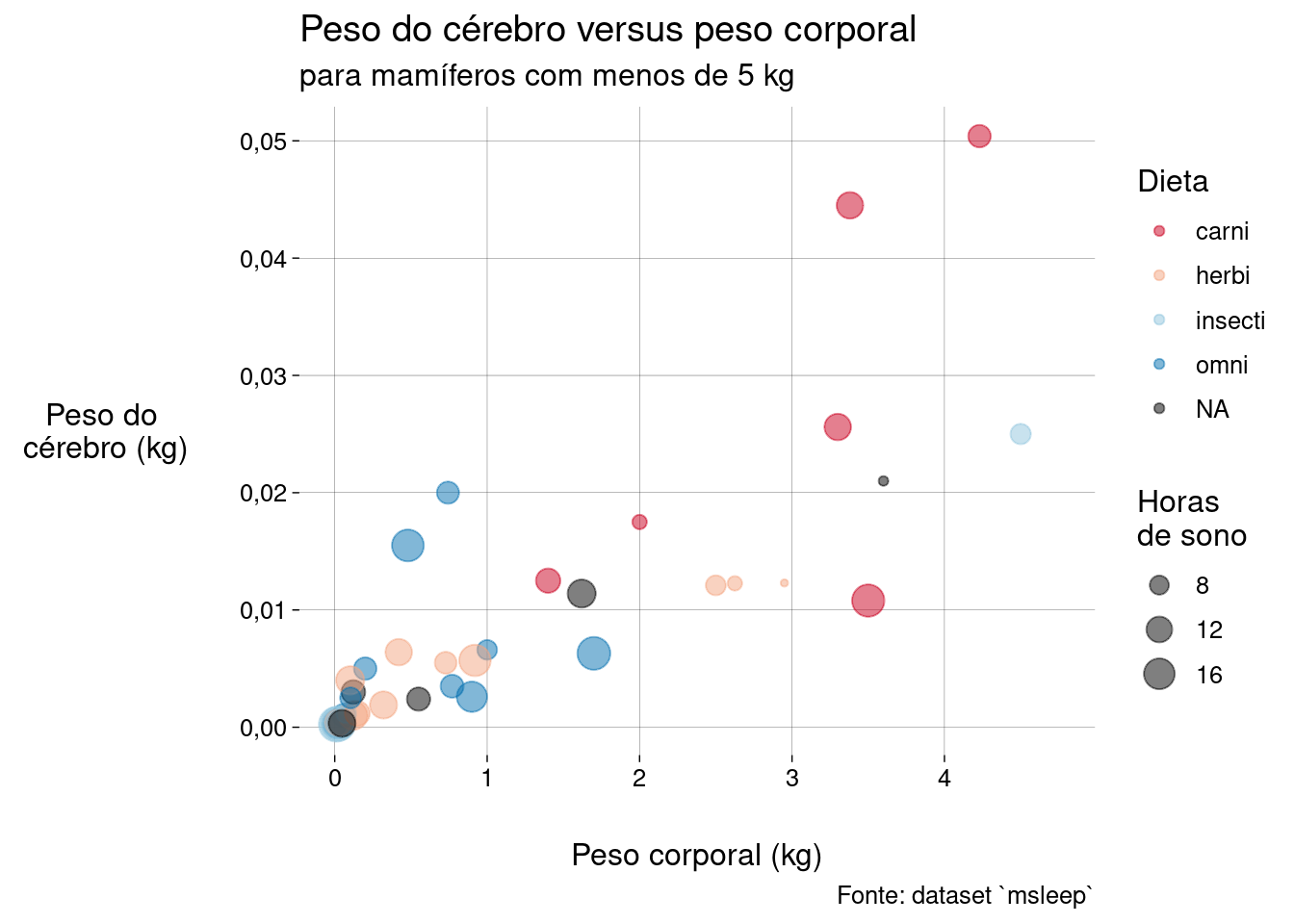

Observe como usamos o gráfico já salvo na variável grafico e simplesmente acrescentamos a nova escala. Este tipo de “montagem” de gráficos ggplot2 é bem conveniente, para evitar repetição de código.
Um último ajuste na aparência: os pontos na legenda “Dieta” estão pequenos demais. Quase não identificamos as cores deles.

Vamos usar a função guides para modificar (override) a estética color — apenas na legenda, não nos pontos mostrados no gráfico, cujos tamanhos representam o número de horas de sono — tornando o tamanho maior. Leia mais sobre override.aes neste link (em inglês).
```
grafico3 <- grafico2 +
  guides(color = guide_legend(override.aes = list(size = 10)))

grafico3
```
```
## Warning: Removed 18 rows containing missing values or values outside the scale range
## (`geom_point()`).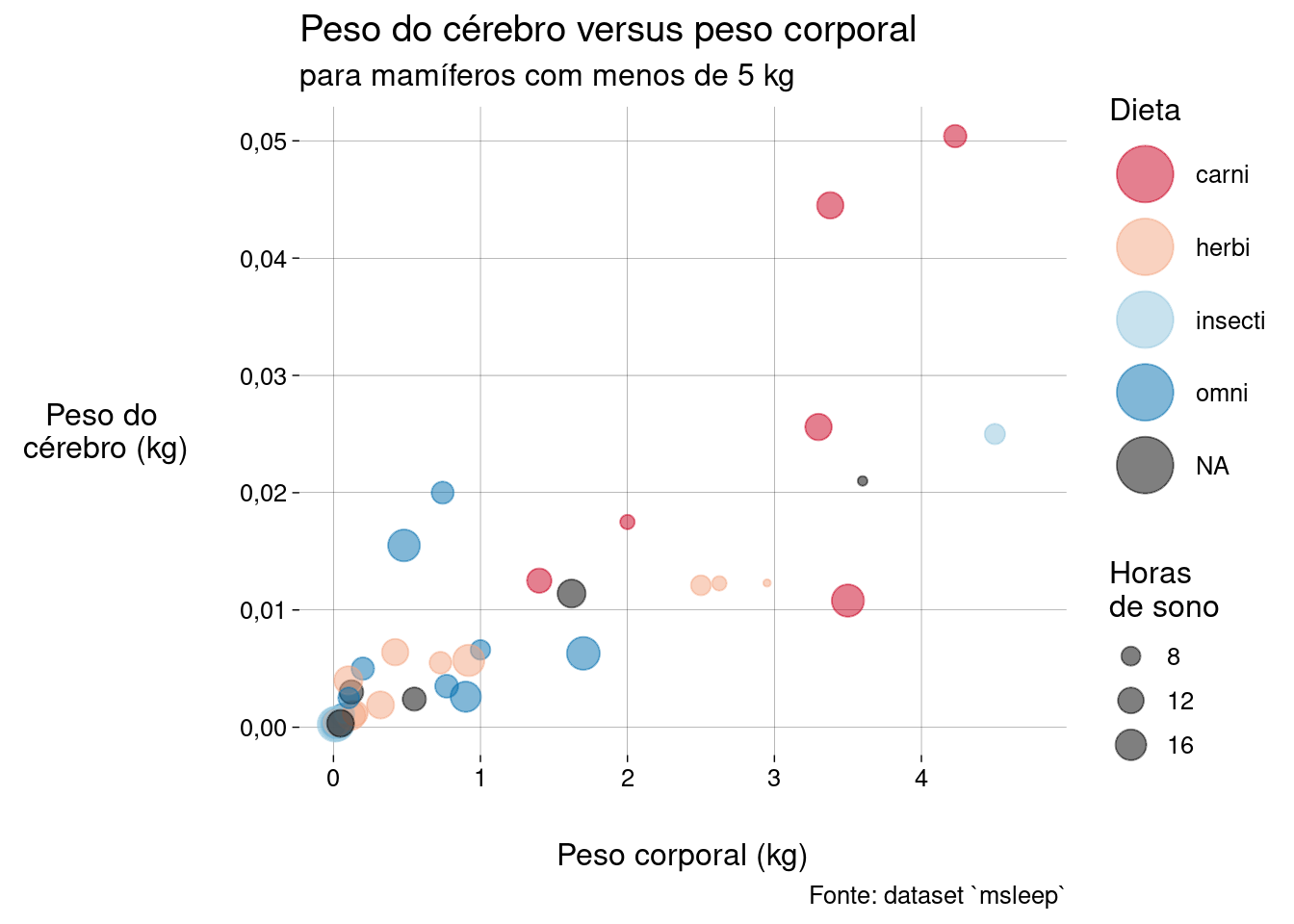
```
Agora podemos finalmente comentar sobre a informação que o gráfico mostra sobre os dados:
- De fato, existe uma correlação entre peso cerebral e peso corporal: quanto maior o peso corporal, maior o peso cerebral. Nada surprenndente.
- Podemos fazer o ggplot2 traçar uma reta de regressão com a geometria geom_smooth. Vamos falar mais sobre correlação em um capítulo futuro.
```
grafico4 <- grafico3 +
  geom_smooth(
    aes(group = 1), 
    show.legend = FALSE,
    method = 'lm', 
    se = FALSE,
    linewidth = 1
  )

grafico4
```
```
## `geom_smooth()` using formula = 'y ~ x'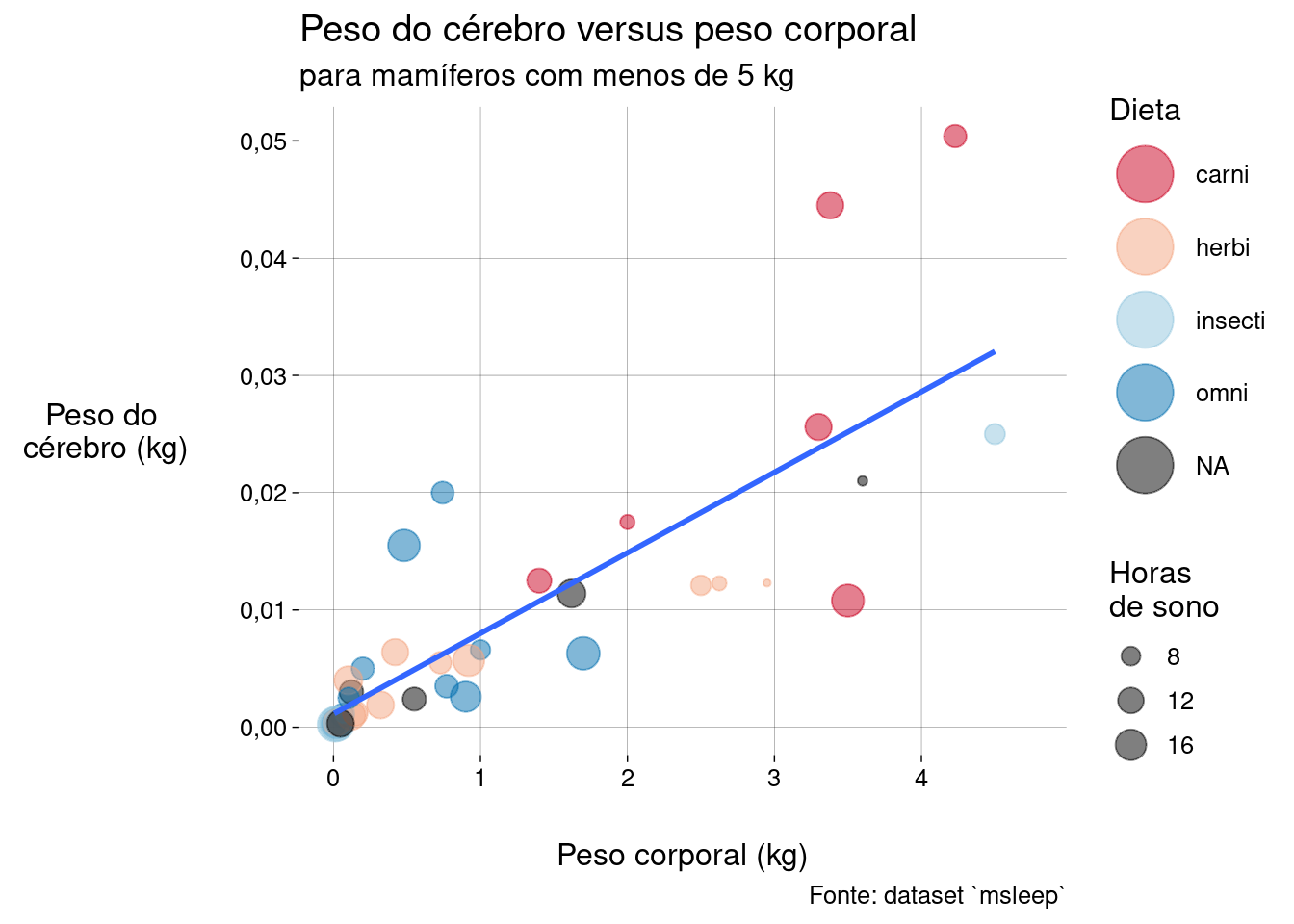
```
- Todos os carnívoros têm peso corporal maior que $1$kg e peso cerebral maior ou igual a $10$g.
- Só um carnívoro dorme $8$ horas ou menos. Qual?
- Todos os insetívoros — com exceção de um (qual?) — são muito leves e dormem muito.
- Todos os onívoros têm menos de $2$kg de peso corporal e $20$g ou menos de peso cerebral.

4.5 Vídeo 2

4.6 Histogramas e cia.

A idéia agora é agrupar indivíduos em classes, dependendo do valor de uma variável quantitativa.

4.6.1 Distribuições de frequência

Vamos nos concentrar nas horas de sono.

sono$sleep_total

##  [1] 12,1 17,0 14,4 14,9  4,0 14,4  8,7  7,0 10,1  3,0  5,3  9,4 10,0 12,5 10,3  8,3
## [17]  9,1 17,4  5,3 18,0  3,9 19,7  2,9  3,1 10,1 10,9 14,9 12,5  9,8  1,9  2,7  6,2
## [33]  6,3  8,0  9,5  3,3 19,4 10,1 14,2 14,3 12,8 12,5 19,9 14,6 11,0  7,7 14,5  8,4
## [49]  3,8  9,7 15,8 10,4 13,5  9,4 10,3 11,0 11,5 13,7  3,5  5,6 11,1 18,1  5,4 13,0
## [65]  8,7  9,6  8,4 11,3 10,6 16,6 13,8 15,9 12,8  9,1  8,6 15,8  4,4 15,6  8,9  5,2
## [81]  6,3 12,5  9,8

Antes de montar o histograma, vamos construir uma distribuição de frequência.
A amplitude é a diferença entre o valor máximo e o valor mínimo. A função range não retorna a amplitude, mas sim os valores mínimo e máximo:
```
sono$sleep_total %>% range()
```
```
## [1]  1,9 19,9
```

Vamos decidir que cada classe vai ter $2$ horas. A função cut substitui os valores do vetor pelos nomes das classes:

sono$sleep_total %>% 
  cut(breaks = seq(0, 20, 2), right = FALSE)

##  [1] [12,14) [16,18) [14,16) [14,16) [4,6)   [14,16) [8,10)  [6,8)   [10,12) [2,4)  
## [11] [4,6)   [8,10)  [10,12) [12,14) [10,12) [8,10)  [8,10)  [16,18) [4,6)   [18,20)
## [21] [2,4)   [18,20) [2,4)   [2,4)   [10,12) [10,12) [14,16) [12,14) [8,10)  [0,2)  
## [31] [2,4)   [6,8)   [6,8)   [8,10)  [8,10)  [2,4)   [18,20) [10,12) [14,16) [14,16)
## [41] [12,14) [12,14) [18,20) [14,16) [10,12) [6,8)   [14,16) [8,10)  [2,4)   [8,10) 
## [51] [14,16) [10,12) [12,14) [8,10)  [10,12) [10,12) [10,12) [12,14) [2,4)   [4,6)  
## [61] [10,12) [18,20) [4,6)   [12,14) [8,10)  [8,10)  [8,10)  [10,12) [10,12) [16,18)
## [71] [12,14) [14,16) [12,14) [8,10)  [8,10)  [14,16) [4,6)   [14,16) [8,10)  [4,6)  
## [81] [6,8)   [12,14) [8,10) 
## 10 Levels: [0,2) [2,4) [4,6) [6,8) [8,10) [10,12) [12,14) [14,16) ... [18,20)

A função table faz a contagem dos elementos de cada classe:
```
sono$sleep_total %>%  
  cut(breaks = seq(0, 20, 2), right = FALSE) %>% 
  table(dnn = 'Horas de sono') %>% 
  as.data.frame()
```

4.6.2 Histograma

Na verdade, o ggplot2 já faz esses cálculos para nós.

O default é criar $30$ classes (bins):

sono %>% 
  ggplot(aes(x = sleep_total)) +
    geom_histogram()

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.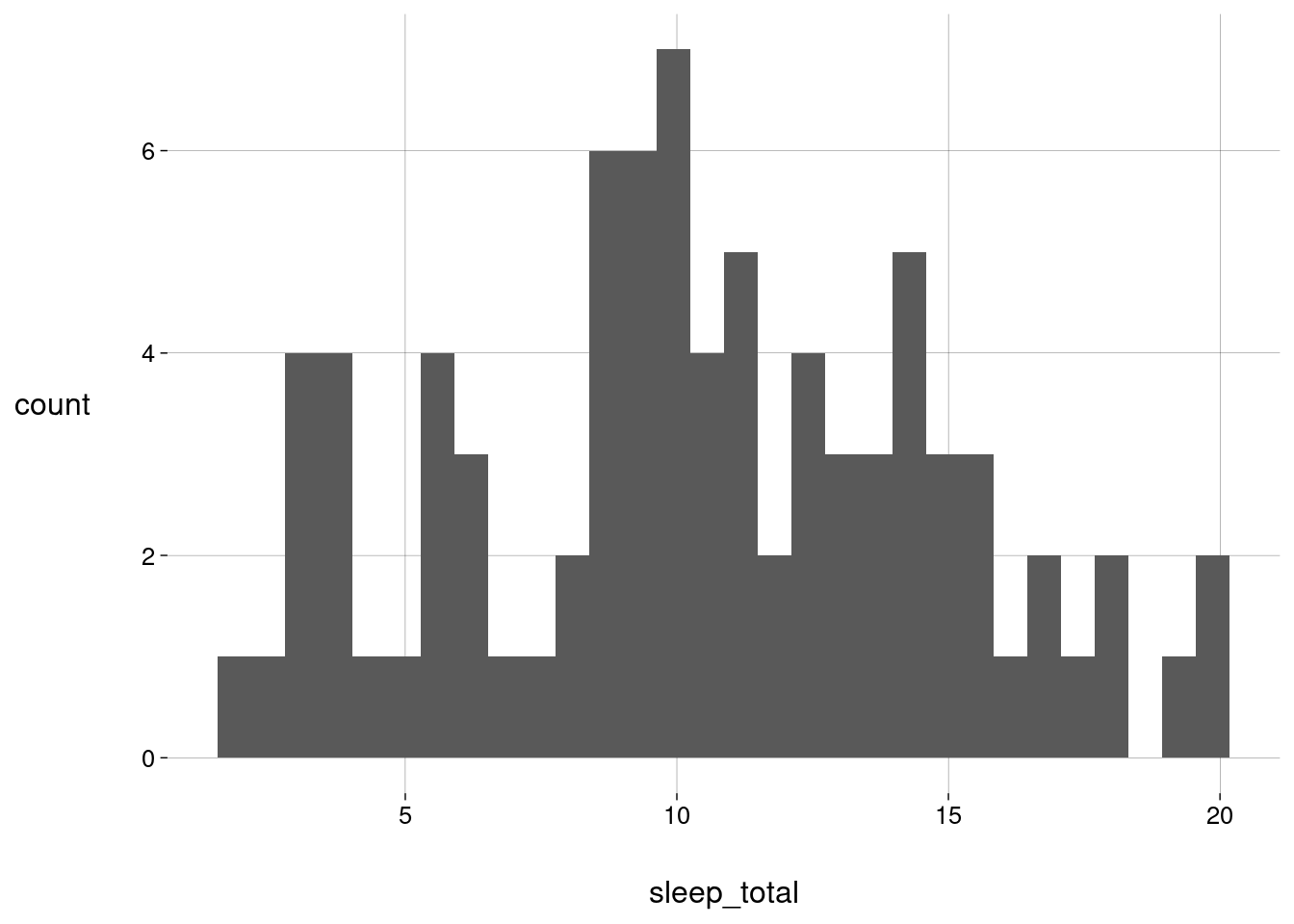

Vamos mudar isto passando um vetor de limites das classes (breaks). Vamos acrescentar rótulos também:

sono %>% 
  ggplot(aes(x = sleep_total)) +
    geom_histogram(breaks = seq(0, 20, 2)) +
    scale_x_continuous(breaks = seq(0, 20, 2)) +
    labs(
      title = 'Horas de sono de diversos mamíferos',
      x = 'horas de sono',
      y = NULL,
      caption = 'Fonte: dataset `msleep`'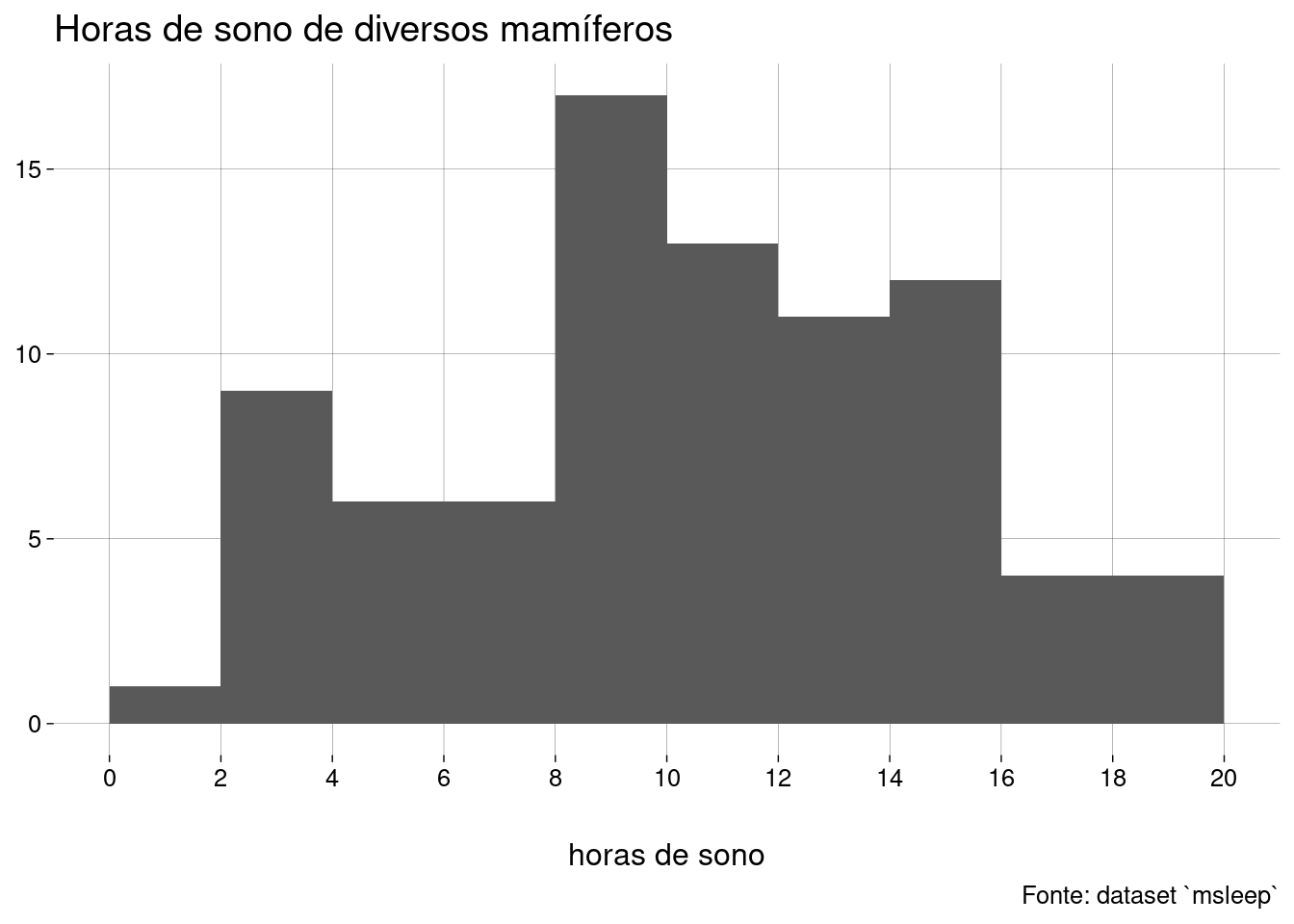
    )

Nossas impressões:
- A classe que mais tem elementos é a de $8$ a $10$ horas.
- A distribuição é mais ou menos simétrica.
- A distribuição tem forma aproximada de sino: há poucos mamíferos com valores extremos de horas de sono; a maioria está próxima do valor médio:
```
mean(sono$sleep_total)
```
```
## [1] 10,43373
```

4.6.3 Polígono de frequência

Em vez das barras do histograma, podemos desenhar uma linha ligando seus topos.

O resultado é um polígono de frequência.

pf <- sono %>% 
  ggplot(aes(x = sleep_total)) +
    geom_freqpoly(breaks = seq(0, 20, 2), color = 'red') +
    scale_x_continuous(breaks = seq(0, 20, 2))

pf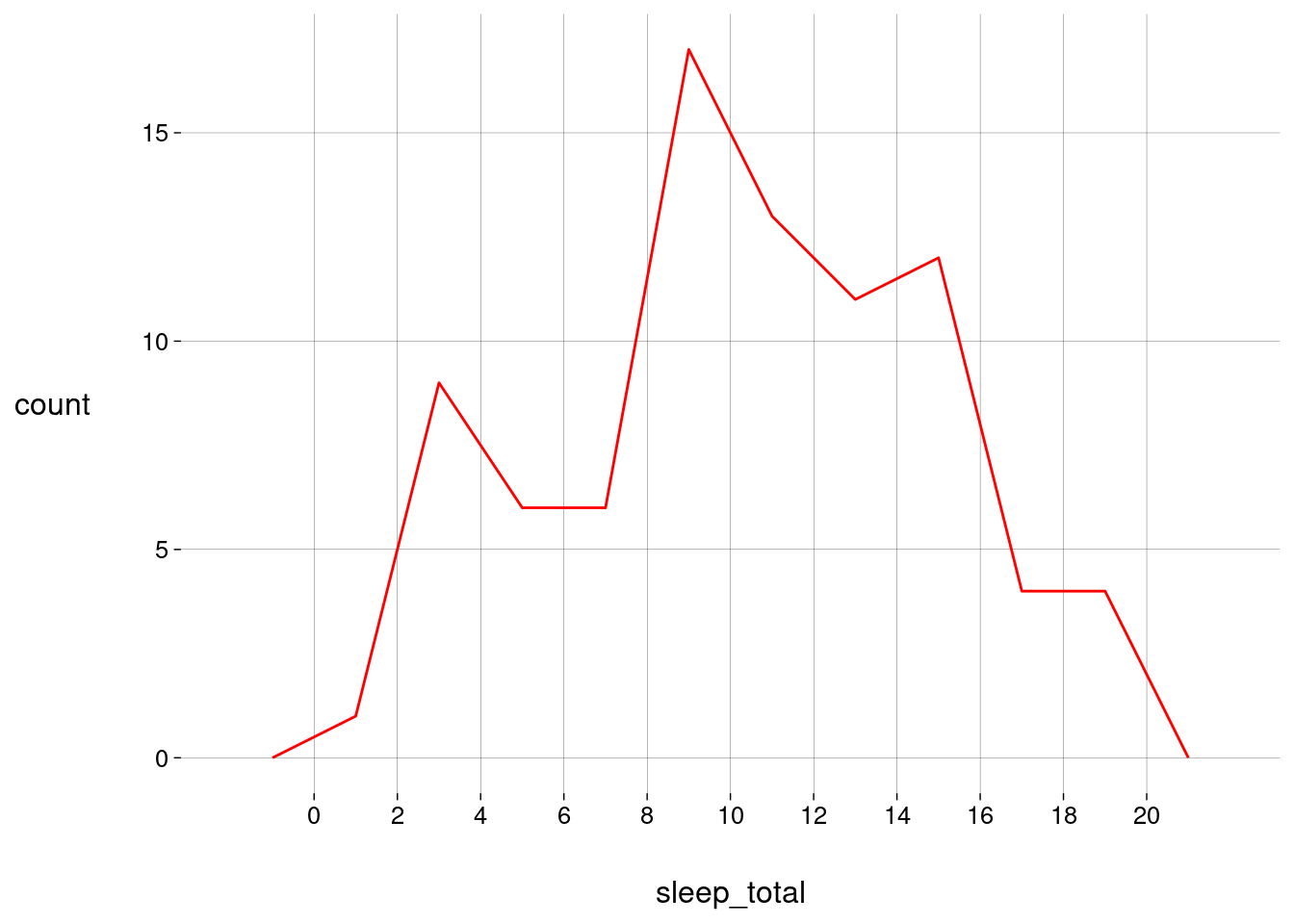

Vamos sobrepor o polígono de frequência ao histograma, para deixar claro o que está acontecendo:
```
pf + geom_histogram(breaks = seq(0, 20, 2), alpha = .3)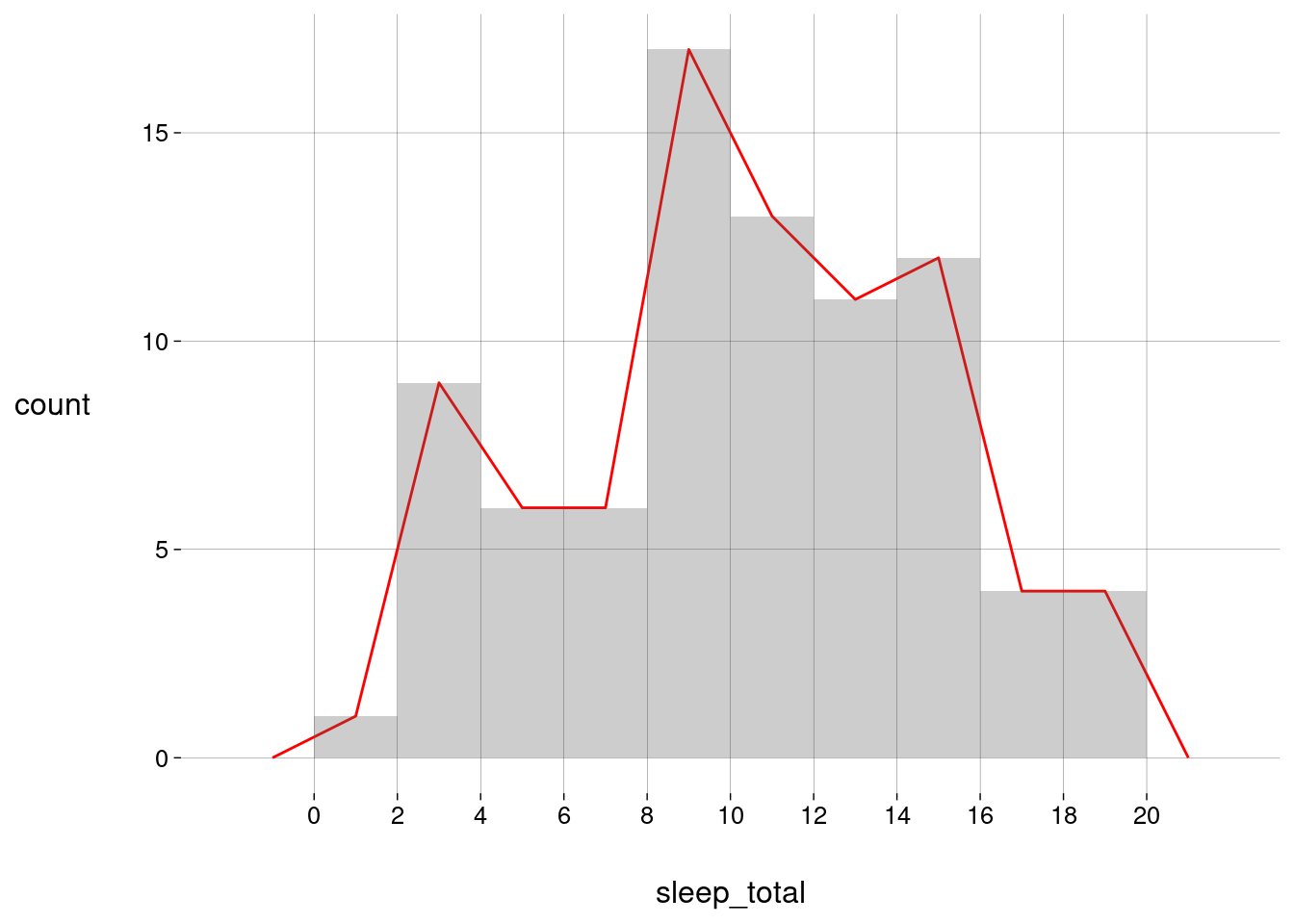
```

4.7 Ogiva

A ogiva é um gráfico que mostra a frequência acumulada: para cada valor $v$ da variável no eixo $x$, a proporção de indivíduos com valor menor ou igual a $v$.
A geometria geom_step gera o gráfico de uma função degrau.
Cada geometria está ligada a uma stat, um algoritmo para computar o que vai ser desenhado. Aqui, passamos para a geometria a função ecdf (empirical cumulative distribution function), do pacote stats, que calcula as frequências acumuladas.
```
sono %>% 
  ggplot(aes(x = sleep_total)) +
    geom_step(stat = 'ecdf') +
    scale_x_continuous(breaks = seq(0, 20, 2)) +
    scale_y_continuous(breaks = seq(0, 1, .1)) +
    labs(y = NULL)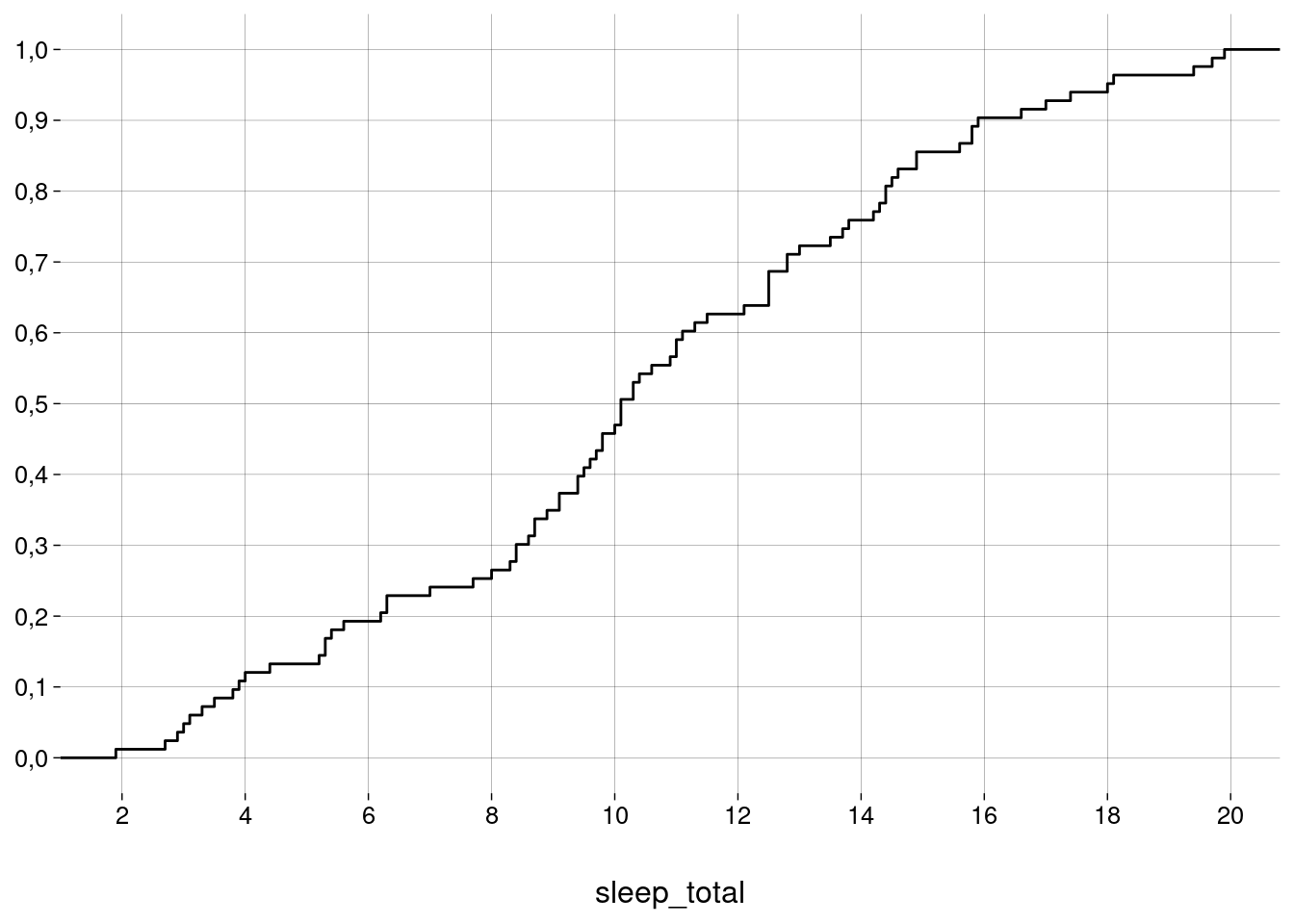
```
Com a ogiva, podemos obter informações difíceis de visualizar no histograma. Por exemplo:
- Cerca de $20\%$ dos mamíferos têm menos de $6$ horas de sono.
- Cerca de metade dos mamíferos têm menos de $10$ horas de sono.
- Cerca de $10\%$ dos mamíferos têm mais de $16$ horas de sono.

4.8 Ramos e folhas

No início dos anos $1900$, quando estatísticas eram feitas à mão, Arthur Bowley criou os diagramas de ramos e folhas.
Um diagrama de ramos e folhas é, basicamente, uma listagem de todos os valores de uma variável, agrupados de maneira que todos os valores de uma classe (i.e., de uma linha) têm os algarismos iniciais dentro de um intervalo.

Para as horas de sono dos mamíferos:

sono$sleep_total %>% 
  stem()

## 
##   The decimal point is at the |
## 
##    0 | 9
##    2 | 79013589
##    4 | 0423346
##    6 | 23307
##    8 | 03446779114456788
##   10 | 01113346900135
##   12 | 15555880578
##   14 | 234456996889
##   16 | 604
##   18 | 01479

A primeira linha representa um indivíduo com $0{,}9$ horas de sono.
A penúltima linha representa $3$ valores:
- $16{,}6$
- $17{,}0$
- $17{,}4$

4.9 Personalização do tema

O ggplot2 tem um tema default, chamado theme_gray, que gera o scatterplot de um exemplo anterior deste capítulo do seguinte modo: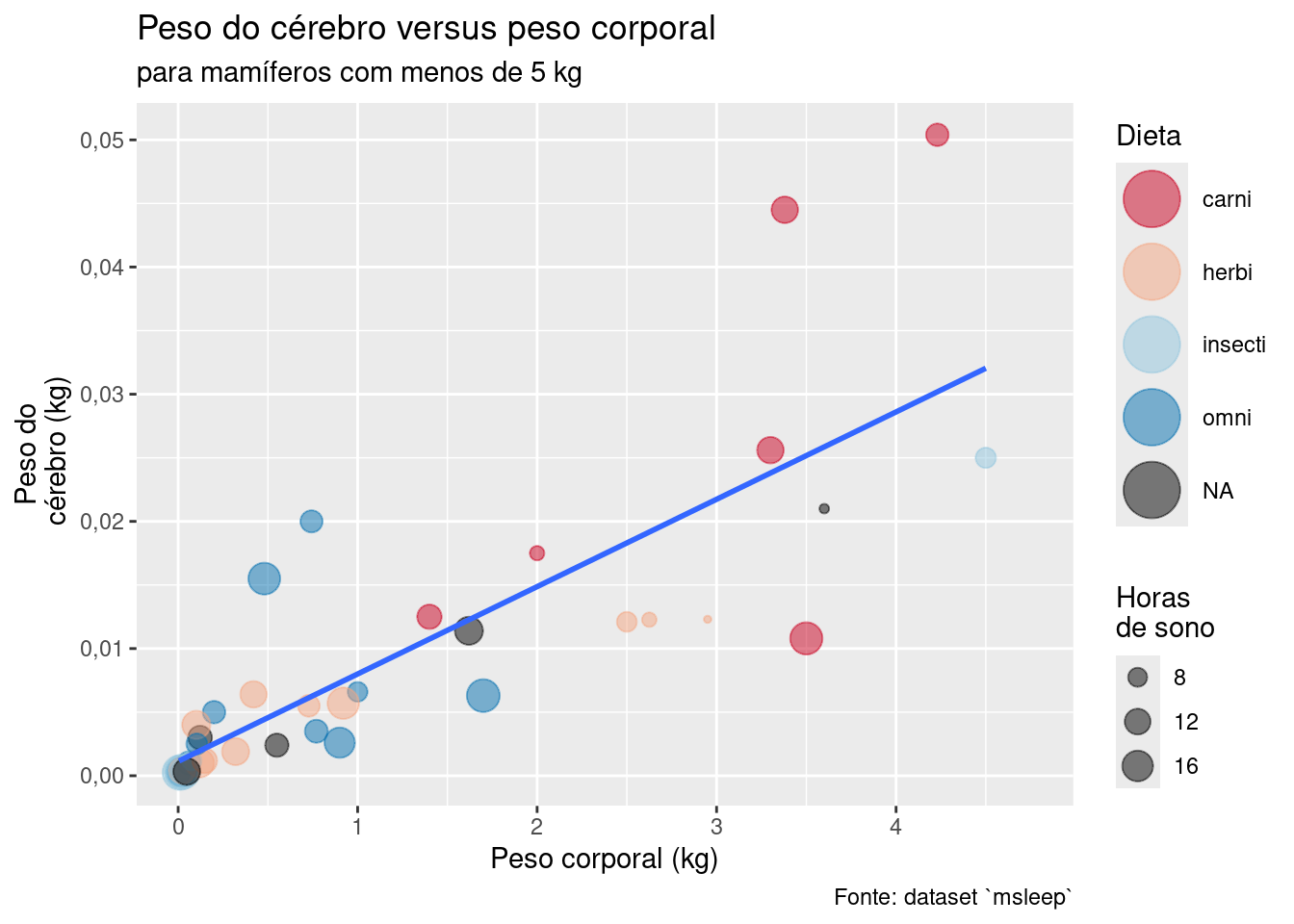
Para este material, escolhi o tema theme_linedraw, que usa linhas pretas sobre fundo branco: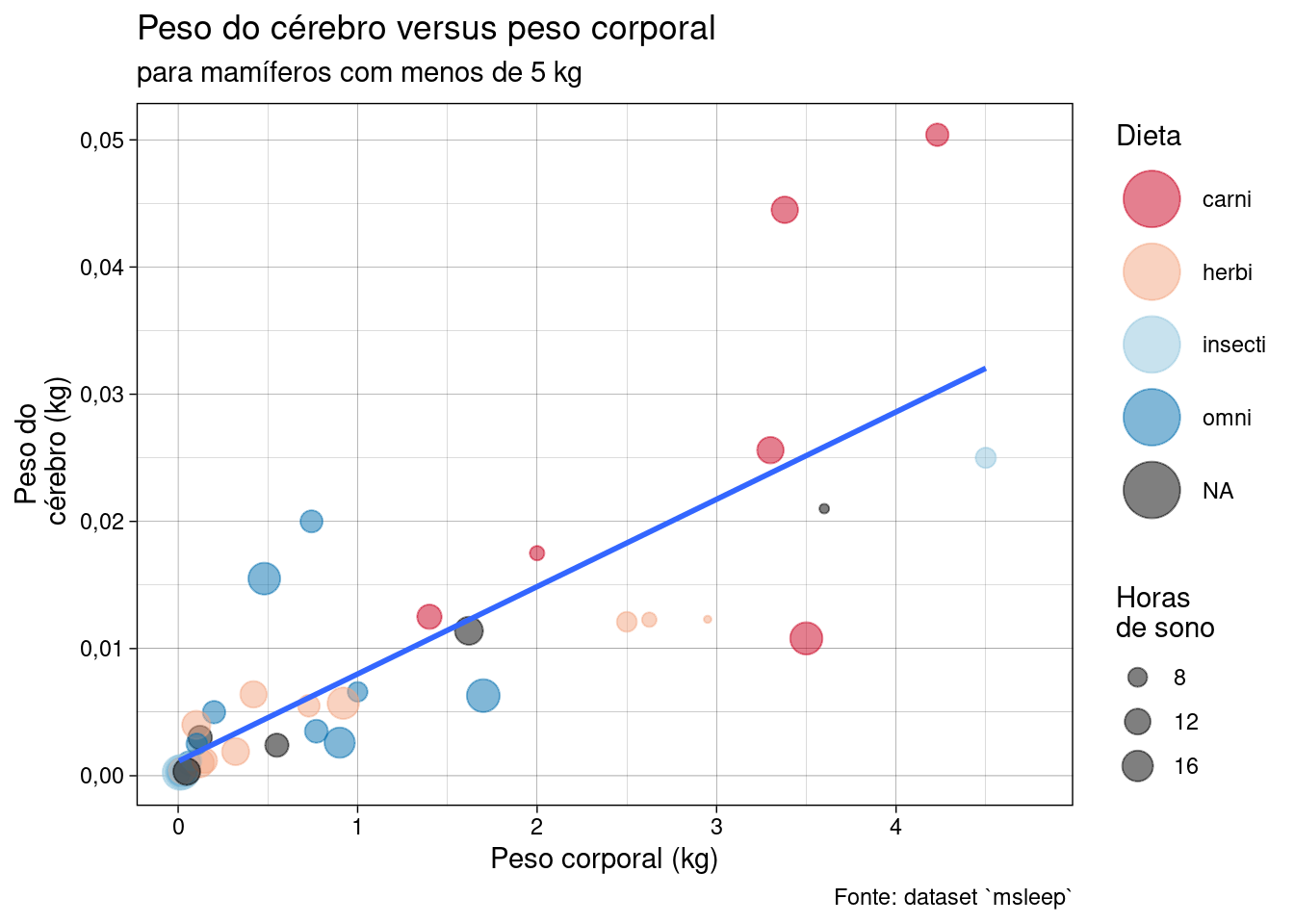
Para deixar os gráficos mais leves e facilitar a leitura, fiz as seguintes alterações no tema:
- Mudei o tamanho do texto dos rótulos.
- Fiz o rótulo do eixo $y$ aparecer na horizontal; embora isto ocupe um pouco mais de espaço, evita que o leitor tenha que girar a cabeça para ler o rótulo.
- Eliminei as linhas dos eixos, para o gráfico ficar mais leve.
- Eliminei a moldura da área de dados, para o gráfico ficar mais leve.
- Eliminei a grade secundária, para o gráfico ficar mais leve.
O resultado é

Os meus comandos para alterar o tema são

# Tamanho do texto depende do formato de saída (html ou pdf):
plot_text_size = ifelse(is_html_output(), 12, 13)

# Tema mais leve:
theme_set(
  theme_linedraw() +
    theme(
      # Tamanho do texto
      text = element_text(size = plot_text_size),
      # Eixo y
      axis.title.y.left = element_text(
        # Nunca girar o rótulo do eixo y
        angle = 0,
        # Separar o rótulo do eixo um pouco
        margin = margin(r = 20),
        # Posicionar verticalmente no meio
        vjust = .5
      ),
      # Eixo y secundário (à direita), quando presente
      axis.title.y.right = element_text(
        # Nunca girar o rótulo do eixo y
        angle = 0,
        # Separar o rótulo do eixo um pouco
        margin = margin(l = 20),
        # Posicionar verticalmente no meio
        vjust = .5
      ),
      # Não colocar marcas no eixo y secundário
      axis.ticks.y.right = element_blank(),
      # Separar o eixo x do rótulo um pouco mais
      axis.title.x.bottom = element_text(
        margin = margin(t = 20)
      ),
      # Eliminar linhas dos eixos
      axis.line = element_blank(),
      # Eliminar a moldura da área de dados
      panel.border = element_blank(),
      # Eliminar a grade secundária
      panel.grid.minor = element_blank()
    )
)

4.10 Exercícios

Não se esqueça de incluir títulos nos gráficos e rótulos nos eixos.

4.10.1 Peso cerebral e peso corporal

Observe os comandos que geraram o gráfico grafico4.
O que acontece se você retirar aes(group = 1) da chamada a geom_smooth? Explique.
O que acontece se você mudar show.legend = FALSE para show.legend = TRUE na chamada a geom_smooth? Explique.
O que acontece se você mudar se = FALSE para se = TRUE na chamada a geom_smooth? Explique.
Acrescente ao gráfico a camada facet_wrap(~vore). O que acontece?
Examine o data frame sono e identifique o único insetívoro com mais de $4$kg.
Instale o pacote gg_repel e acrescente ao gráfico grafico4 (não facetado) a geometria geom_label_repel (consulte a ajuda) para rotular o mamífero insetívoro identificado no item anterior com o seu nome, sem cobrir outros pontos do gráfico. Cuidado para não alterar a legenda que já existe.

4.10.2 Peso cerebral e horas de sono

Use o data frame sono definido como

library(ggplot2)

sono <- msleep %>% 
  select(
    name, order, genus, vore, bodywt, 
    brainwt, awake, sleep_total
  )

Construa um histograma da variável brainwt. Escolha o número de classes que você achar melhor. O que acontece com os valores NA?
Descubra que função da forma scale_x_... usar para fazer com que o eixo $x$ tenha uma escala logarítmica. Gere um novo histograma.
Qual dos dois histogramas é melhor para responder a pergunta “Qual a faixa de peso cerebral que tem mais animais?” de forma satisfatória?
Construa um scatter plot de horas de sono versus peso do cérebro. Você percebe alguma correlação entre estas variáveis? Se precisar, concentre-se em um subconjunto dos dados.
Usando geom_smooth (leia a respeito), sobreponha uma reta de regressão ao gráfico de dispersão, usando o método lm e sem o erro-padrão (i.e., com se = FALSE). O que você observa? Discuta.

4.10.3 Igualdade de gênero entre furacões?

Este artigo tenta achar uma relação entre o gênero do nome de um furacão e a quantidade de vítimas fatais provocadas por ele.

Os dados estão no pacote DAAG, que deve ser instalado:

if (!require(DAAG))
  install.packages("DAAG")

Vamos usar apenas algumas das variáveis, com nomes em português.

df <- hurricNamed %>% 
  as_tibble() %>% 
  transmute(
    id = paste(Year, Name, sep = '-'),
    nome = Name,
    ano = Year,
    velocidade = LF.WindsMPH * 1.8,     # convertido para km/h
    pressao = LF.PressureMB,            # mbar
    prejuizo = BaseDam2014 %>% round(), # milhões de dólares de 2014
    mortes = deaths,
    genero = mf
  )

Crie histogramas para as seguintes variáveis, escolhendo a quantidade de barras que você achar melhor.
- velocidade
- prejuizo
- mortes
Não se esqueça de incluir títulos nos gráficos e rótulos nos eixos.

Comente os histogramas.
Os histogramas de prejuízos e mortes não ficaram bons. Vamos gerar histogramas transformados.

No data frame, crie duas novas colunas:
- logprejuizo: logaritmo do prejuízo (na base $10$)
- logmortes: logaritmo do número de mortes (na base $10$)
Agora, gere histogramas destas duas novas variáveis.
O que significa o valor do logaritmo do prejuízo na base $10$?
O que significa o valor do logaritmo do número de mortes na base $10$?
Por que o histograma do logaritmo do número de mortes vem com uma mensagem de aviso?
Por que isto não acontece com o logaritmo do prejuízo?
Faça um gráfico de dispersão com pressao no eixo $y$ e velocidade no eixo $x$.
Usando geom_smooth (leia a respeito), sobreponha uma reta de regressão ao gráfico, usando o método lm e sem o erro-padrão (i.e., com se = FALSE). O que você observa? Discuta.
Faça um gráfico de dispersão com logmortes no eixo $y$ e pressao no eixo $x$.
Usando geom_smooth (leia a respeito), sobreponha uma reta de regressão ao gráfico, usando o método lm e sem o erro-padrão (i.e., com se = FALSE). O que você observa? Discuta.
Faça um gráfico de dispersão com logmortes no eixo $y$ e pressao no eixo $x$, com pontos coloridos de acordo com o gênero do nome do furacão.
Usando geom_smooth (leia a respeito), sobreponha retas de regressão ao gráfico, uma para cada gênero, usando o método lm e sem o erro-padrão (i.e., com se = FALSE). O que você observa? Discuta.

Visualizações como esta ajudam a explorar os dados, mas não servem para testar rigorosamente a hipótese de que furacões mulheres matam mais do que furacões homens.

Mais adiante no curso, vamos aprender a fazer testes mais rigorosos sobre hipóteses como esta.

3 Introdução ao tidyverse

5 Visualização com ggplot2 (continuação)